단순 선형 회귀 (Simple Linear Regression)

기준 모델 (Baseline Model)

예측 모델을 구체적으로 만들기 전에 가장 간단하면서 직관적이고, 최소한의 성능을 나타내는 기준이 되는 모델

• 분류문제 : 타겟의 최빈 클래스
• 회귀문제 : 타겟의 평균값
• 시계열회귀문제 : 이전 타임스탬프의 값

예측 모델 (Predictive Model)

산점도에 가장 잘 맞는(best fit) 직선을 그려주면 그것이 선형 회귀 예측모델이 된다.

단순 선형 회귀 모델

$y =$ 반응(response)변수, 레이블(label), 타겟(target)
$x =$ 예측(predictor)변수, 설명(Explanatory), 특성(feature)
$\alpha =$ 회귀 계수, 즉 기울기
$\beta =$ 절편 y의 시작값
$\epsilon =$ 오차

잔차 (Residual)

잔차는 예측값과 관측값 차이

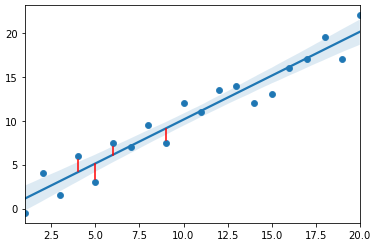
위의 그림과 같은 빨간 선을 우리는 선형 회귀 모델의 잔차라고 한다.

최소제곱법 OLS (Ordinary Least Squres)

잔차 제곱합을 최소화 하는 방법

회귀선은 잔차 제곱들의 합인 RSS(Residual Sum of Squres)를 최소화 하는 직선
RSS는 SSE(Sum of Squres)라고도 말하며 이 값이 회귀모델의 비용함수(Cost function)이 된다.
머신러닝에서는 비용함수를 최소화 하는 모델을 찾는 과정을 학습이라고 한다.

RSS

$\sum_{i=1}^n(\varepsilon_i)^2 = \sum_{i=1}^n(y_i - f(x_i))^2 = \sum_{i=1}^n(y_i - \alpha{x_i} + \beta)^2$

$\alpha$와 $\beta$는 RSS를 최소화 하는 값으로 모델 학습을 통해서 얻어지는 값

계수 계산을 위한 OLS의 식

$\beta = \bar{y} - a\bar{x} \\{}\\ \alpha = {S_{xy} \over S_{xx}} \\{}\\ S_{xy} = \sum_{i=1}^n(x_i - \bar{x})(y_i - \bar{y}) \\{}\\ S_{xx} = \sum_{i=1}^n(x_i - \bar{x})^2$

식의 참고[네이버 수학산책 최소제곱법]

MSE와 MAE

MSE = Mean Squared Error

$MSE = {1 \over n}\sum_{i=1}^n(\hat{x}_i-x_i)^2$

MAE = Mean Absolute Error

$MAE = {1 \over n}\sum_{i=1}^n|\hat{x_i} - x_i|$