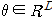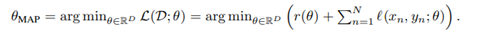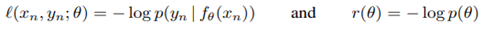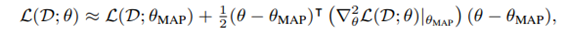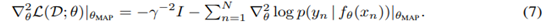안녕하세요 ai 학부연구생입니다. 주로 weights에 대해 연구(사실상 공부)를 진행하고 있고, 따라서 관련 최신 논문들을 리뷰하고 기록하고자 합니다. 그 중 요새 주로 공부하고 있는 베이지안 Deep Learning과 관련하여 라플라스 근사를 이용하고 실제로 훌륭한 성능을 보인 논문에 대해 이야기하고자 합니다.
0. Abstract
딥러닝의 베이지안은 실용적인 이득과 경쟁력 있는 이론적 가치들을 보여 왔습니다. 예를 들어 예측 불확실성의 향상된 정량화와 모델의 선택에 있어 그런 점들을 보여 왔죠. 그리고 논문에서 계속 다룰 Laplace approximation (LA)는 다루기 힘든 DNN의 posteriors의 추정에 있어 논의할 수 있는 가장 단순한 모형입니다. 논문에서는 이러한 베이지안 딥러닝과 LA를 추론으로 엮어 생각해보고자 합니다.
LA는 단순함에도 불구하고 베이즈나 딥러닝 앙상블과 같은 방법에 대안으로 인기 있지 않습니다. 아마도 LA가 주로 헤시안 계산에 있어 expensive하고, 실제 적용하기에 어려움이 있으며, 결과마저 비교적 열등하기에 그럴겁니다. 하지만 이런 의견들이 오해이자 편견이라고 본 논문의 연구진들은 이야기하고 싶어합니다. 다음은 오해를 풀기 위해 연구진이 제시한 논문의 방향성입니다.
(i) 연구진은 우선 minimal cost를 가진 버전을 포함하는 LA의 다양한 범위에 대해 이야기합니다.
(ii) 그 후 LA에 대해 유저친화적인 접근을 제공하는 PyTorch library 소프트웨어인 laplace를 소개합니다.
(iii) 그리고 실제적인 실험을 통해서 LA가 경쟁력 있고 좀 더 퍼포먼스 측면에서 인기 있을 대안임을 증명합니다. 탁월한 계산적 효율성은 그 덤입니다.
1. Introduction
여러 성공에도 불구하고, 현대의 신경망은 여전히 적용성을 제한하는 몇몇 문제점들을 겪고 있습니다. 첫째, 데이터 분포가 training에서 testing로 변할 때 잘못된 보정과 overconfidence를 수반합니다. 둘 째, 새로운 작업에 대해 지속적으로 훈련을 받을 때 이전에 학습한 작업에 대해 치명적인 망각이 일어납니다. 그리고 셋 째, 신경망의 구조와 하이퍼 파라미터의 적절한 선택에 있어 어려움을 가지고 있습니다.(아마 초기값?) 첫번 째와 세번 째 같은 경우는 저처럼 이제 막 연구를 시작한 사람도 익히 알고 있는 큰 문제점입니다.
베이지안 모델링은 강력한 불확실성 추정치를 제공하고, 모델이 과거 정보를 이용하여 지속적으로 학습할 수 있도록 하며, 데이터 적합성과 모델의 복잡성을 절충함으로써 자동화된 모델을 선택합니다. 이러한 특징들로 위에 제시한 문제들을 해결하기 위한 원칙적인 접근 방식을 제공합니다. 하지만, BNNs가 이러한 장점들을 가지고 있음에도, 실제 상황에서 그다지 많은 프로젝트에 사용되지 못했습니다. 일반적으로 BNNs을 비판하는 사람들은 BNNs가 실제로 적용하는 데 있어 어렵고, 튜닝도 까다로우며, train에 있어 expensive하고, 현대의 모델과 데이터셋의 스케일에 적용하기 어렵다고 말합니다. 실제로도 기존의 베이지안 방법들은 위와 같은 문제들을 가지고 있는데 반해, 앙상블, 몬테칼로 드롭아웃, SWAG과 같은 방법들은 비교적 간단한 방법으로 불확실성을 추정합니다. 그렇다고 위 방법들이 마냥 능사는 아닙니다. 비용이나 경험적 성능 그리고 베이지안 해석의 측면에서 만족스럽지 않다는 문제들이 있습니다.
위 같은 방법들의 대안으로 연구진은 Laplace approximation (LA)가 단순하고 비용 측면에서 효율적이며 베이지안 딥러닝의 추론을 위한 경쟁력 있는 근사방법이라고 주장합니다. (간단하게만 말하면 LA는 곡률에 해당하는 공분산 행렬을 사용하여 로컬 최대값을 중심으로 하는 가우시안 분포로 posterior를 근사합니다. 그리고 이 posterior를 구하고 다시 prior로 사용하여 다음 posterior를 구하는 과정을 반복하여 추론하는게 베이지안의 핵심입니다.)
LA의 두 가지 주요 이점은 로컬 최대값이 MAP(maximum a possteiori) training으로부터 쉽게 구해진다는 것과 곡률 추정이 (헤시안 행렬에 대해 효율적인 근사를 하기위해서 그리고 좀 더 이용하기 편한 소프트웨어 라이브러리의 관점에서) 쉽고 효율적으로 얻을 수 있다는 것입니다. 곡률 얻는 데 있어 second-order optimization의 최근 발전 덕분이라네요. 네 잘 모르겠습니다. 그런 동향이 있는지는 몰랐네요. ㅎㅎ
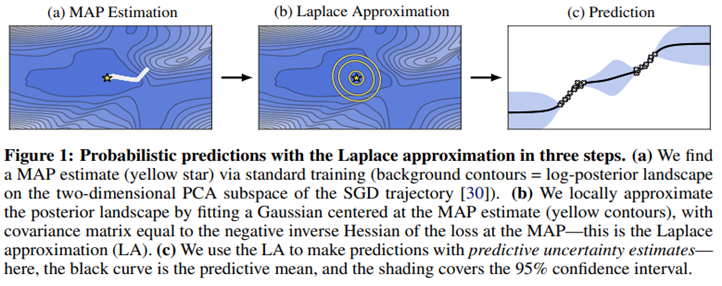
다음은 LA의 직관적인 이해를 돕기 위한 그림입니다.
(1)SGD 궤적을 PCA를 통해 축소한 2차원 부분공간에서 트레이닝을 통하여 MAP estimate를 찾습니다. 노란색 별로 표시되어 있는 지점입니다!
(2) 노란색 별을 중심으로 적합한 가우시안 분포를 fitiing하여 posterior의 locally하게 추정합니다.
(3) 이제 LA를 이용하여 에측불확실성 추정과 함께 추정치들을 만듭니다. 검은색 줄은 평균을 칠해진 커버부분은 95% 범위를 의미합니다.
2. The Laplace Approximation in Deep Learning
LA는 딥러닝의 이점을 위해 두 가지 방식으로 사용될 수 있습니다. 한 가지는 확률적 예측을 가능하게 하는 model’s posterior distribution의 근사에 사용하는 것이고, 나머지 한 가지는 model 선택을 가능하게 하는 model evidence의 근사에 사용하는 것입니다. 다음은 각각 앞서 소개한 두 가지 방식에 대한 수식입니다. 각각을 (5), (6)이라 하겠습니다.
우선 Introduction에서 소개한 대로 MAP estimate를 행합니다. 그 후 log와 likelihood를 이용하여 posterior를 최대로 하는 θ를 찾는데, 이 방식에 대해 잠시만 이야기하겠습니다. 우선 i.i.d.인 classification dataset 그리고 가중치값을 잡습니다. 그리고 정규화된 경험적 리스크를 최소화하는 방식으로 앞서 잡은 가중치값을 train하는 함수를 잡습니다.각각 다음과 같습니다.
그리고 이 경험적 리스크는 경험적 loss terms
l(x_n, y_n ; θ)와 regularizer r(θ)의 합으로 분해됩니다. 그 수식은 다음과 같습니다. 각각 (1), (2)라 합시다.
(1) 을보면 θ_MAP가 loss terms과 regularizer의 합을 최소화하는 θ로 선택된 것을 볼 수 있습니다.
이제 LA를 이해하는데 필요한 수학적 재료들은 준비가 끝났습니다. 이미 θ_MAP이 MAP estimate이기 때문에 우선 가장 먼저 구해야할 MAP estimate를 구하는 과정은 생략하겠습니다 ㅎㅎ. 위 재료들로 예를 들어보면 폭넓게 쓰이는 weight regularizer r(θ) = -ʮ^(-2) ||θ||^2, (a.k.a weight decay)는 가우시안 prior P(θ) = N(θ; 0, (ʮ^2)I)와 대응됩니다. 참고로 가우시안에서 prior은 하나의 함수가 아니라 저렇게 분포로 표현됩니다! 함수가 분포를 가지고 있다고 생각하면 됩니다. 그 분포에서 하나의 함수를 그때그때 택하게 됩니다.
cross-entrophy loss는 범주형 likelihood에 속하며 따라서 expotential of the negative training loss, exp(-L(D;θ)은 normalized 되지 않은 posterior에 해당합니다. 그리고 이것을 normalzing하면 다음과 같은 수식 (3)을 얻을 수 있습니다.
(해당 식은 연속형 변수인 경우의 베이즈 정리에 의해 간단하게 나타낼 수 있습니다.)
여기서 LA는 p(θ|D)에 대하여 가우시안 근사를 구성하기 위해 근처의 second-order expansion of L을 이용합니다.
계산 결과 우리는 위와 같은 식(4)을 고려할 수 있습니다. 위 식과 (3), (5)식을 고려하면, 결국 the approximate posterior를 얻기 위해서 log-posterior function에서 θ_MAP을 얻어야 함을 알 수 있습니다. 그 후 다음 스텝은 그저 헤시안 행렬의 역연산을 계산하는 것 뿐이죠.
일반적으로 두 번 미분가능한 log-density는 헤시안 연산에서 prior로 사용할 수 있습니다. 따로 언급이 없는 경우에는 zero-mean을 가지는 가우시안을 이용하여 prior, p(θ)를 고려합니다. 널리 쓰이는 regularizer로 weigh decay가 있는데 이 weight decay가 l2 정규화이기 때문에 prior이 정규화된 것입니다. 그래서 prior의 평균이 0이 나오게 됩니다.
최종적으로 헤시안은 log-prior(regilarizer)와 log-likelihood(empirical risk)에 의존합니다. 다음 식을 (2)와 (4)와 함께 고려하면 이해할 수 있을겁니다. 다음 식을 보면 (4)식을 두번 미분한 사실을 알 수 있습니다.
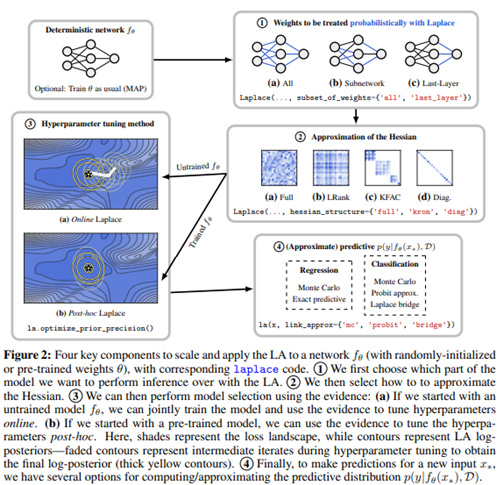
다음으로 본 논문은 LA가 modern deep architecture에서 잘 수행하고 확장될 수 있도록 하는 네 가지 주요 구성요소에 대해 설명합니다. 구성요소를 살펴보면 다음과 같습니다.
① 모든 가중치 값 혹은 가중치 값의 부분집합에 대한 추론
② 헤시안 근사와 factorizations
③ 하이퍼 파라미터의 튜닝
④ 예측 분포 근사
위 그림은 laplace에 대한 대략적인 설명이자 앞서 언급한 4가지 구성요소가 포함된 각 순서의 방법을 순서대로 표현한 모습입니다. 거기에 더해 각 챕터마다 현재 이용할 수 있는 code에 대해 간략하게 적어놨습니다.
① 모든 가중치값 혹은 가중치 값의 부분집합에 대한 추론
대부분의 경우 헤시안의 적절한 근사치를 사용할 때 모든 가중치를 확률적으로 처리하는 것이 가능합니다. 이에 대한 내용은 ②에서 다룰 예정입니다. 또한 LA를 대규모 네트워크로 확장하는 간단한 방법은 가중치의 부분 집합만 LA로 확률적으로 처리하고, 나머지는 MAP 추정 값으로 남겨두는 것입니다.
② 헤시안 근사와 factorizations
수식 (7)의 두 번째 항에서 신경망의 log-likelihoods를 헤시안으로 0이상의 근사를 하게되면 LA가 이점을 얻을 수 있다고 합니다. 이 방법은 second-order optimization을 발전시킨 방법 중 하나입니다. log-likelihoo를 헤시안으로 근사할 때 이용하기 좋은 행렬의 예시로 fisher-info-matrix와 GGN matrix를 소개하는데, 이 두 행렬은 수학적으로 계산하는 과정에서도 헤시안과 유사합니다. 특히 피셔 정보 행렬의 경우 헤시안의 기대치값으로 떨어지게 됩니다. 이러한 이유로 직접 헤시안을 구하는 것은 너무 헤비하니 이렇게 다른 행렬로 우회해서 헤시안과 관련된 정보를 수집하는 겁니다. 그리고 Figure2에 나와있는 정보처럼 헤시안을 근사하는 방법으로 행렬을 블록 단위로 나눠 보거나 대각성분만 처리하는 방법으로 헤시안의 근사치를 구하곤 합니다.(KFAC)
③ 하이퍼 파라미터의 튜닝
당연한 소리지만 모든 근사 추론 방법에 있어서 LA의 성능은 prior과 likelihood의 하이퍼 파라미터에 의존합니다. 예를 들어 prior variance를 튜닝하는 것이 하지 않는 것보다 여러모로 장정을 가지고 있습니다. 하지만 하이퍼 파라미터를 튜닝할 때 일반적으로 분포 외의 데이터를 이용하거나 log-likelihood를 최대화하여 교차 검증을 해야합니다. 하지만 LA를 사용할 때 marginal likelihood maximization 방법은 하이퍼 파라미터를 튜닝할 때 원칙적인 대안을 내놓고, 검증 데이터도 필요 없습니다. (관련논문: Scalable Marginal Likelihood Estimation for Model Selection in Deep Learning) 그리고 또 다른 LA에 대한 하이퍼 파라미터 튜닝으로 베이지안 최적화나 불확실성 조정만을 목적으로 하는 hidden units을 추가하는 방법이 있습니다.
④ 예측 분포 근사
생략
3. laplace: A Toolkit for Deep Laplace Approximations
LA를 구현하기 위해선 계산도 효율적이어야하고, 헤시안도 저장해야합니다. 간단한 작업은 아닙니다. 아주 어려운건 아니지만 모든 요소에서 만족할만한 구현은 존재하지 않습니다. 대신 딥 러닝에서는 다양하고 효율적인 방법으로 LA와 Hessian 계산을 반복하여 구현합니다. 하지만 구현한다해도 효율적이기 위해선 수백 줄의 코드가 필요하므로 LA로 빠르게 무언가를 만드는 건 어렵습니다. 이에 대한 해결책으로 본 논문은 PyTorch에서 DNN으로 확장 가능한 라이브러리인 laplace를 소개합니다. 논문에 나와있는 그림은 두 가지 코드 예제를 보여주고, 핵심적으로 필요한 LA posterior과 marginal likelihood, posterior predictive 이 세가지의 효율적인 구현에 대해서 설명합니다. 추가로 대부분의 사례에 대해 적용하기 위해 어떻게 구상하였는지까지 설명하고 있습니다.
해단 섹션에서 나오는 라이브러리 laplace의 단점만 잠깐 짚고 넘어가겠습니다. 백엔드로 라이브러리를 사용하다보니 라이브러리에서 선택 가능한 Hessian Factorization만 사용가능합니다. 새로운 방식의 Hessian Factorization이 지원되지 않는 거죠. 예를 들어 kafc를 지원하지 않기 때문에 LA변형은 현재 구현이 불가합니다. 마찬가지로 첫 번째 버전은 아직 subnetwork LA에서 지원하지 않습니다. 음... 한계점이라기 하기엔 사소한 것들만 적어놨네요. 업데이트를 해주면 되는거 아닌가 싶습니다.
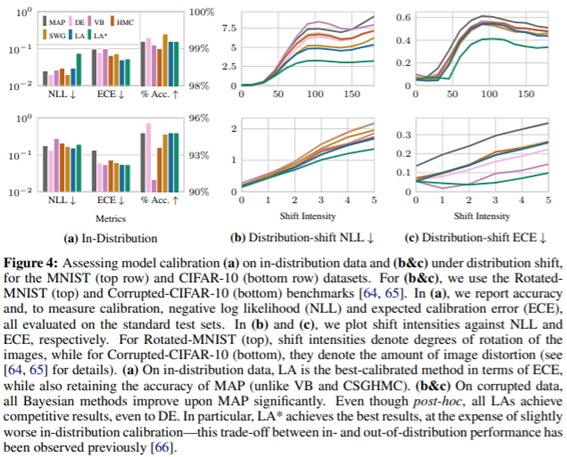
4. Experiments
정확도도 준수하고 ECE측면에서는 제일 훌륭합니다. NLL에 경우는 약간 높게 나왔네요! 하지만 ID가 아닌 Ddistribution-shift에서는 NLL에서도 뛰어난 성능을 보입니다.
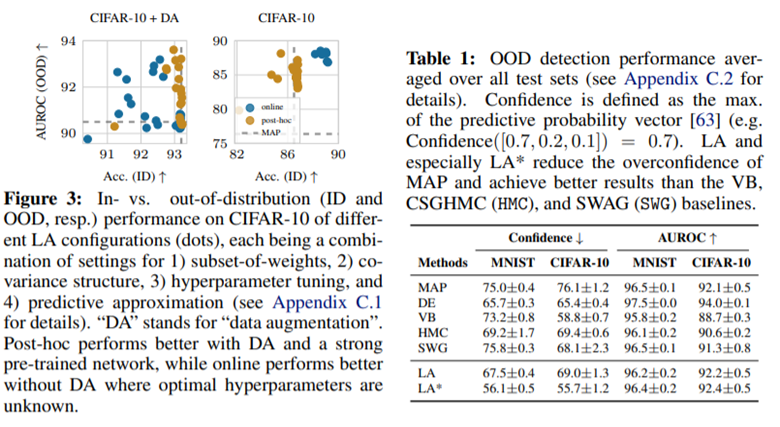
다른 방식들에 비해 confidence는 더 낮고 대신 AUROC는 유사한 것을 볼 수 있습니다.
p.s. 논문에 대한 공부를 끝마치자마자 3월14일에 ver3가 올라왔습니다.
Reference: Laplace Redux – Effortless Bayesian Deep Learning
https://arxiv.org/pdf/2106.14806.pdf