여담
정말 멍청하게도 SCPC 2022 예선기간을 날짜를 착각해서 놓쳤다. 😂 이번엔 본선 도전해보려고 했었는데, 내년에 복학해서 마지막 ACM-ICPC 도전과 함께 SCPC, UCPC, SUAPC 등등 다시 나가봐야겠다. (이번해엔 쉬자!)
이렇게 된거 Model Garden Project 밀린거랑 Adversarial Auto Encoder나 짜봐야겠다...
사실 알고리즘 관련해서는 나보다 더 문제를 잘풀고, 깔끔한 설명들이 많지만 개인적으로 이렇게라도 안하면 백준을 전혀 안풀것같아서 틈틈이 적어보려고 한다. DP로 시작하는 이유는, 현재 취미로 하고있는 스터디에서 마침 Dynamic Programming을 계획으로 진행하기때문에 해당 자료를 만들겸 겸사겸사...
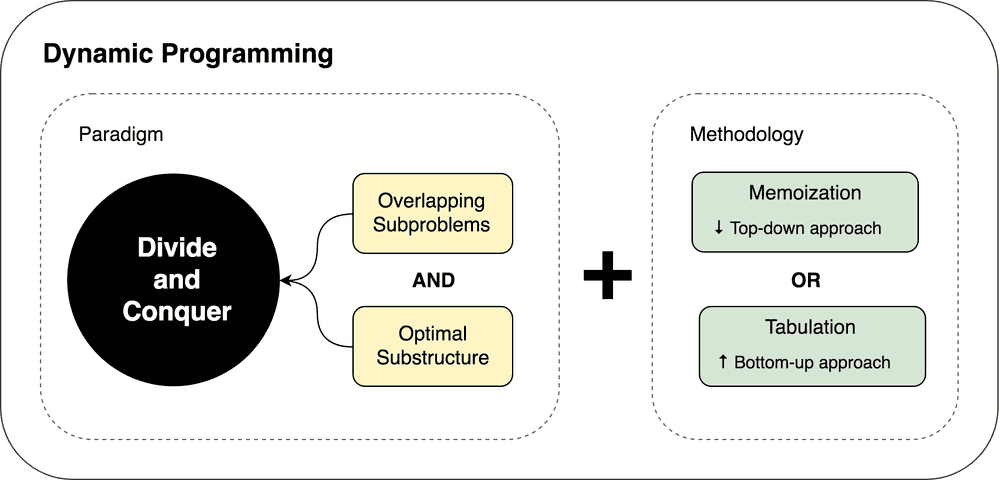
Dynamic Programming (동적 계획법)
부분문제반복과 최적부분구조를 가지고 있는 문제에대해 복잡한 문제를 간단한 여러개의 문제로 나누어 푸는 방법
여러개의 문제로 나누어 푸는 방법이라는 점에서 분할정복 (Divide-and-Conquer) 이랑 유사하다고 생각하고, 처음 접할때는 두가지가 비슷한게 아니라는 생각이 든다. 분할정복과 마찬가지로, 작은 부분문제 (Subproblem)로 나누어서 푼다는 점에서 공통점이 있다고 생각한다. 동적계획법 또한 완전탐색등의 방법으로 지나치게 비효율적으로 해결되는 문제를 효율적으로 해결하기 위해 점화식 등의 방법으로 효율적으로 문제를 해결하기 위해 고안된 아이디어이다.
해당 문제가 Dynamic Programming 인지 알려면 크게 두가지를 알아야 한다고 생각한다.
1) Overlapping Subproblems (부분 문제 반복)
먼저, 알고리즘을 분명하게 알고있는 사람들이라면 문제를 풀면서 두개의 차이점을 분명하게 알고있겠지만, 처음 문제를 풀게되는 경우 해당 차이점을 인지하기 힘들다.
분할정복의 경우, 두개의 subproblem 끼리 겹치는 교집합이 없는 경우가 대부분이다. ( 거의 없다라고 표현하는 이유는 문제 설계를 어떻게 하냐에 따라서 Conquer 과정에서 처리해주는 과정이 교집합이 있다 라고 다룰 수 있기 때문이다. )
동적 계획법 같은 경우에는 작은 부분 문제가 반복되는 상황이 일어난다. 분할정복과 결정적인 차이점인데, 일종의 이미 해결한 subproblem에 대한 정답이 지속적으로 요구된다 && 문제 상황에서 교집합이 생긴다 두가지중 어떤 방식으로 이해해도 상관없을 듯 하다.
2) Optimal Substructure Property
전체의 최적해는 부분문제의 최적해들로부터 도출 될 수 있어야한다.
작은 문제에서 구한 정답은 해당 상황을 포함하는 더 넓은 상황에 대해서도 무조건 같은 정답이 나와야한다는 의미이다.
만약, 부분문제들의 최적해들로 도출 될 수 없다면, 해당 문제는 Dynamic Programming 으로 설계될 수 없다는 뜻이기도 하다. 아래 문제들의 예시들로 따져보도록 하자.
Problem1 - BOJ 1003 (피보나치 함수)
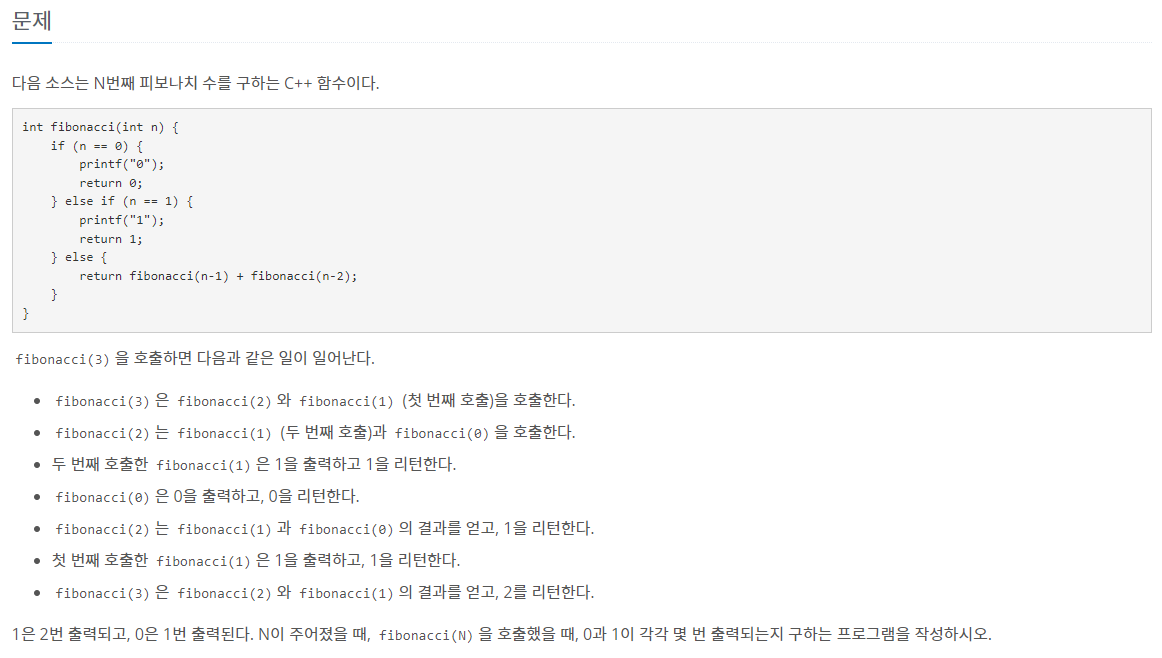
기본 피보나치 함수를 해결하는 것보다 더 친절하게 Top-Down 방식으로 구현된 예시 코드가 존재한다. 만약 해당 방식을 분할정복으로 생각하려고 한다면, 어떻게 나눠야 할지 막막하다.
이분 탐색처럼 중간값을 기준으로 구해야할지? 아쉽게도 끝항은 전 2개의 항에 지속적인 영향을 받기때문에 중간에 subproblem 정답을 얻어놓기가 힘들다. 따라서, 위와 같이 Top-Down 방식으로 구현되어있는 코드를 개량 시키는 방법이 필요하다.
만약 문제에서 주어진 방식대로 , n 까지 함수를 구한다면 시간복잡도는 이 된다.
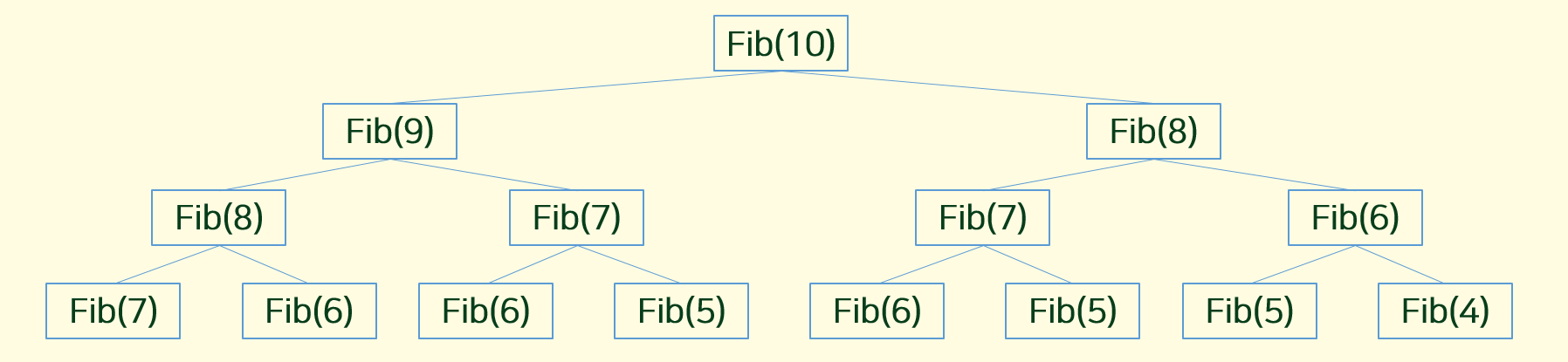
위와 같이 모든 2가지 경우에 대해서 N까지 모두 찾아봐야하기 때문에 완전탐색의 시간복잡도가 된다.
해당 문제를 Subproblem으로 나누어보자.
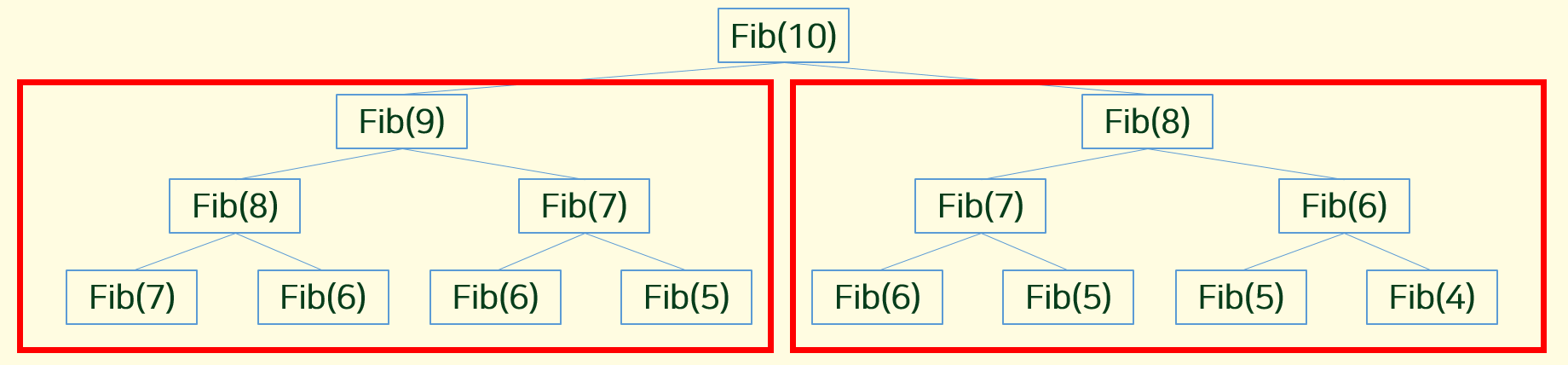
Fib(10)을 구하는 과정은 Fib(9) 를 구하는과정과, Fib(8) 을 구하는 과정으로 볼 수 있다. 이때, 같은 색으로 칠한 박스는 동일한 깊이의 함수 (위의 코드를 참고하면 재귀로 구현이 되어있기때문에) 에서 호출되는 것을 나타내기 위해서 같은 색으로 표시를 했다.
해당 문제가 분할정복 (Divide and Conquer) 이 작동되지않는 이유는 아래의 그림을 통해서 알아보자.
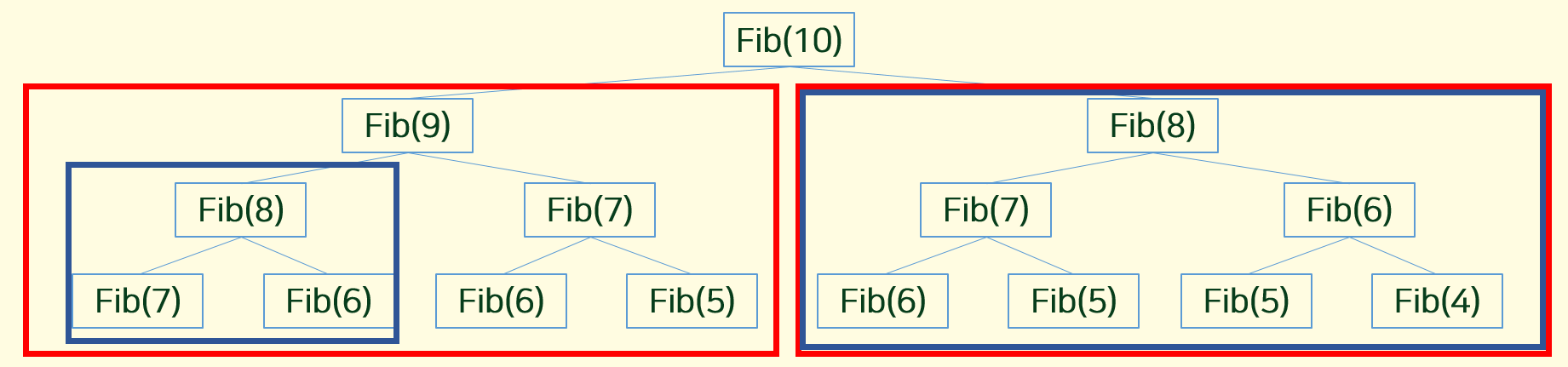
Fib(9) 값을 구할때를 지켜보면 Fib(8)을 구하게된다. 그러나, 우린 Fib(10)에서 값을 구할때 Fib(8)값이 또 필요하다. 만약, 해당값을 따로 저장해주지 않았다면 Fib(8) 만큼을 구할때 만큼의 시간을 또 기다려야 한다.
즉 Dynamic Programming 에서 조건중 하나인 Overlapping Subproblems 이다.
그렇다면, Fib(8)을 여기서 구하게 되면 나중에 해당값은 전체 값을 구할때 여전히 Optimal Substructure를 가질까? 피보나치 함수 같은 경우에는 전항 값을 지속적으로 사용하기 때문에 이에 해당 되는 것을 알 수 있다. 즉, 미리 구해진 값에 대해서 미리 마킹 을 해주고, 만약에 과거에 해결한적이 있는 문제 (마킹 이외의값) 라면, 해당 값을 호출해 오는 방식으로 코드를 개선시킬 수 있다.
int fib(int n) {
// Base Case
if (n == 0) {
printf("0");
return dp[0] = 0;
}
else if (n == 1) {
printf("1");
return dp[1] = 1;
}
else {
// Not Found Yet
if (dp[n] == -1) {
printf("%d", dp[n]);
return dp[n] = fib(n - 1) + fib(n - 2);
}
//Found Before
else return dp[n];
}
}
memset(dp, -1, sizeof(dp));해당 경우는 피보나치에서 0이 이미 등장하는 수이기 때문에, 사전에 모든 배열을 -1로 마킹을 해줬다. 위와 같이 계산하면 발견한 적이 없는 경우에 대해서만 피보나치 수를 계산하고, 이미 해결했던 문제에 대해서는 dp 배열에 Memo 되어있기 때문에 보다 효율적으로 계산이 가능하다.
미리 값을 저장한다는 의미로 해당 방식을 Memoization 이라고 한다. (처음에는 Memorization 인줄 알았다... 메모라이제이션(X), 메모이제이션(O))
다시 본문의 문제로 돌아가자
0과 1을 호출하는 횟수는 fib(0) fib(1)이 몇번씩 호출되냐는 의미이며, 몇가지 케이스에 대해서 생각을 해보면 Fib(n)을 호출할때 걸린 0, 1 횟수 = Fib(n-1)을 호출할때 걸린 0,1 횟수 + Fib(n-2)를 호출할때 걸린0,1 횟수라는 것을 알 수 있다.
위코드를 살짝만 개선시켜도 정답을 얻을 수 있을 것 같다.
Top - down:
#include<bits/stdc++.h>
using namespace std;
pair<int, int> dp[101010];
int t;
int n;
pair<int,int> fib(int n) {
// Base Case
if (n == 0) {
dp[0].first = 1;
dp[0].second = 0;
return { 1,0 };
}
else if (n == 1) {
dp[1].first = 0;
dp[1].second = 1;
return { 0, 1 };
}
else {
// Not Found Yet
if (dp[n].first == -1 && dp[n].second == -1) {
dp[n].first = fib(n - 1).first + fib(n - 2).first;
dp[n].second = fib(n - 1).second + fib(n - 2).second;
return dp[n];
}
//Found Before
else return dp[n];
}
}
int main() {
memset(dp, -1, sizeof(dp));
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
printf("%d %d\n", fib(n).first, fib(n).second);
}
return 0;
}이번에는 다른 관점으로 Bottom-up 으로 풀어볼까 한다.
위 점화식을 살펴보게 되면 N까지 구하는 과정에서 무조건 아래 케이스들에 대해서 정답을 얻어야 한다.
전체 문제를 해결하기 위해서는 하위 문제들이 반드시 해결되어야한다
해당 관점에 입각하여, 미리 하위 문제들 부터 쌓아 올라가보도록 하자.
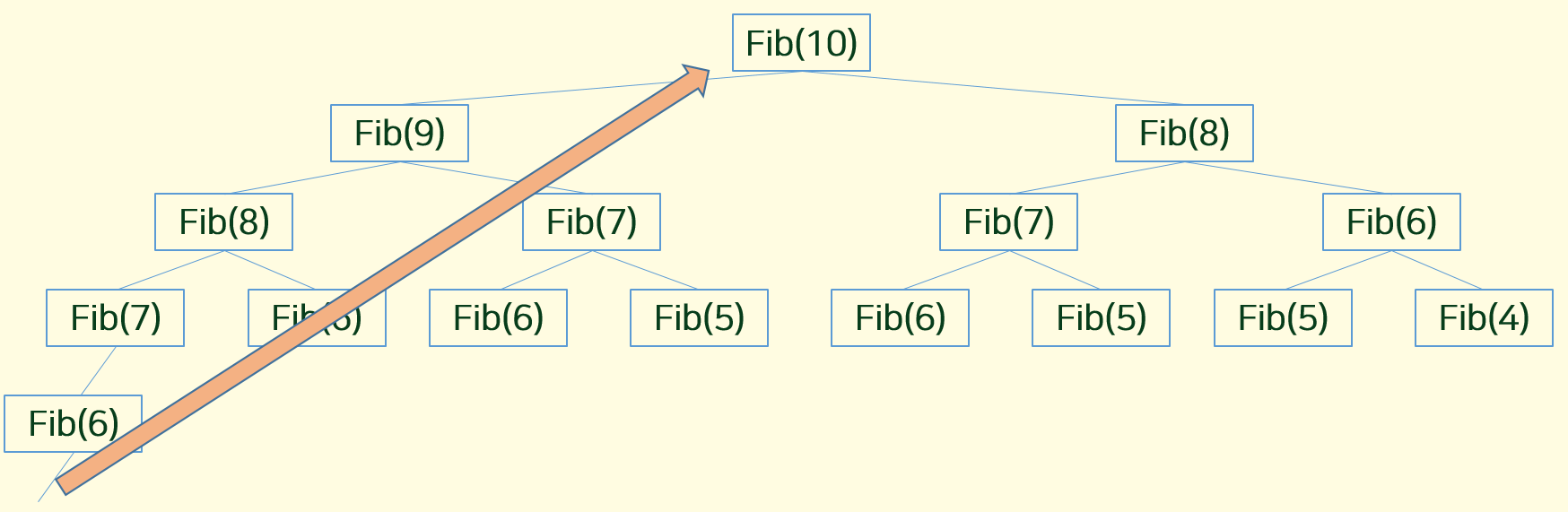
위 해결방식과 차이점은
Top-Down : N을 구하려다보니, 해결 안되어있는 하위문제들을 해결해야하는 과정,
fib39, fib 38 값을 아직 모른다
...
Bottom-Up : 어차피 하위문제들을 해결해야하니깐 미리 하위 문제들을 해결해놓고 답만 출력하자
라는 관점 차이가 있다.
...
그렇다면 Bottom-Up 으로 문제를 살펴본다면 어떤 관점일까? 미리 0, 1에 대한 케이스를 알고있기 때문에, 해당 문제의 최대 입력값인 40까지 미리 정답을 저장하자는 과정으로 생각할 수 있겠다.
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
int dp[2][50];
int main() {
scanf("%d", &t);
dp[0][0] = 1;
dp[0][1] = 0;
dp[1][0] = 0;
dp[1][1] = 1;
for (int i = 2; i <= 40; i++) {
dp[0][i] = dp[0][i - 1] + dp[0][i - 2];
dp[1][i] = dp[1][i - 1] + dp[1][i - 2];
}
while (t--) {
scanf("%d", &n);
printf("%d %d\n", dp[0][n], dp[1][n]);
}
return 0;
}이와 같이 아래부터 조각조각 채워넣는 과정을 Tabulation 이라고 한다. Tabulation이 조금 더 꼼꼼하게 존재할 수 있는 모든 subproblem에서 찾는 것 같지만, 사실 Top-Down이랑 큰차이는 없다. 단지, 관점 차이에 따라서 위와 같이 재귀적으로 짜게 될 경우 Top-Down 형식을 따르게 되고, Base Case 로 부터 결론을 도출해내게 되면 Bottom-up인 경우가 된다.
Top - Down : Memoization
Bottom - Up : Tabulation
기본적인 케이스로부터 생각을 했을 때, 가장 큰 경우부터 생각하기 쉬운 경우 Top-Down, 가장작은 경우로부터 쌓아올라가는 것이 쉬운 경우는 Bottom-up 으로 생각하면 되겠다.
Problem2 - BOJ 9465 (스티커)

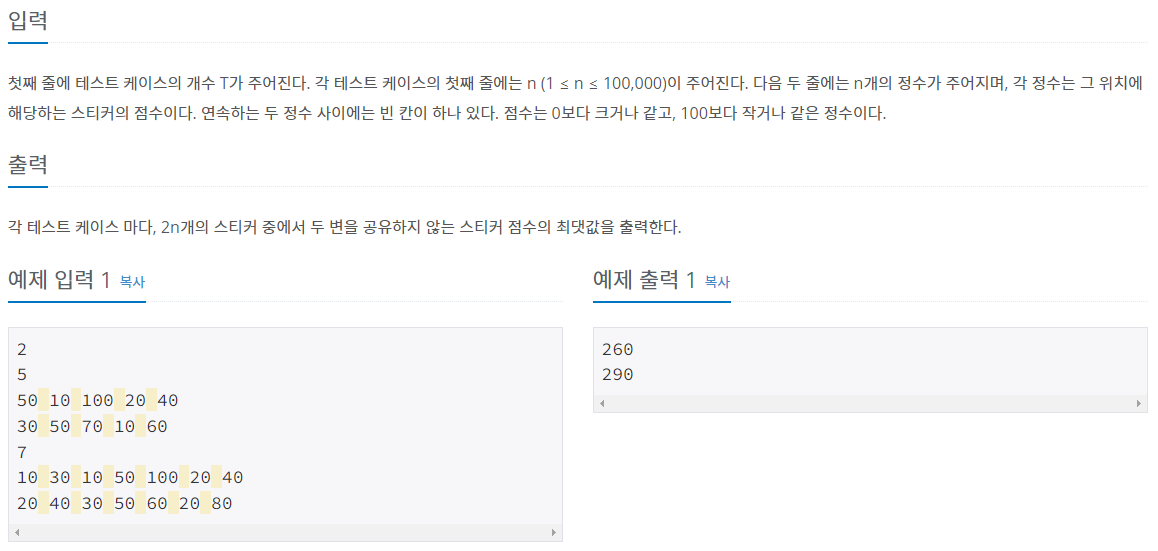
기초적인 DP 문제인 피보나치 뒤에, 2차원 배열로 상태를 관리하는 예제를 준비했다. 아마, 처음 DP를 접하게 되면 1차원배열에 상태를 집어넣는 방법만 생각하게 되는데, 해당 방법을 통해 2차원 배열을 통한 상태 관리와 상태에 따른 점화식을 생각해보자.
점화식 1
N번째 줄에 대해서 우리가 선택할 수 있는 행동은 총 3가지가 있다.
0) N번째 열에서 위에 스티커를 제거하고 점수를 얻는다.
1) N번째 열에서 아래 스티커를 제거하고 점수를 얻는다.
2) 아무 스티커도 선택하지 않고 넘긴다.
만약 서로 변을 공유하지않는 스티커 라는 조건이 없었더라면 단순한 Greedy 문제로 변하게 되며 각 열에서 얻을 수 있는 최대 가치의 스티커를 가져가면 된다. 하지만 변을 공유하고 있기 때문에 현재 내가 어떤 선택을 하게 되면 다음 선택은 과거 선택에 영향을 받게 된다. 즉, 현재 포기하는 선택이 나중에 최대치의 스티커를 제거할 수 있는 기회가 될 수 있다.
dp의 상태를 아래와 같이 정의하자.
dp[0][N] : N번째 열에서 위에 스티커를 제거했을때, 지금까지 얻은 최대값
dp[1][N] : N번째 열에서 아래 스티커를 제거했을때, 지금까지 얻은 최대값
dp[2][N] : N번째 열에서 스티커를 제거하지않았을때, 지금까지 얻은 최대값
사실 다른 글들을 보면 dp[2][N]을 정의하지 않은 경우가 많다. 그러나, 가장 직관적으로 문제를 해결하기 위해서 현재 선택할 수 있는 행동 들을 기준으로 DP 식을 세우려고 했다.
만약 N번째에서 위에 스티커를 제거했을 때, dp[0][N]이 최댓값을 유지하고 싶다면 어떻게 구현하면 될까? 현재 스티커를 제거할 수 있는 상태 0 이므로, 앞선 N-1번째 열 상태인 1 (아래 스티커 제거) 와 상태 2 까지만 고려하면 된다. 이때, 두 상태중 최댓값을 골라서 현재 스티커의 가치를 더해준다면, dp[0][N]는 위에 스티커를 제거하면서 얻을 수 있는 N번째 열까지 최댓값 이 된다.
dp[0][N] = max(dp[1][N-1], dp[2][N-1]) + cost[0][N]
마찬가지로 상태 1 은 아래 스티커를 제거해준 상태이므로, N-1 번째 열 상태 0 과 상태 2에 대해서 update를 해주면 된다.
dp[1][N] = max(dp[0][N-1], dp[2][N-1]) + cost[1][N]
그렇다면 N번째 열에서 선택하지 않았을 경우가 정답이라면? ( 아직 탐색하지않은 오른쪽 열에 가치가 엄청 클경우 현재 선택하지 않는것이 최적해가 된다 ) 해당 경우를 고려해주기 위해 상태2 도 똑같이 업데이트 해준다.
dp[2][N] = max(dp[0][N-1], dp[1][N-1], dp[2][N-1])
여기서 잠시 생각을 해보면 좀 더 식을 개량 시킬 수 있다. 3가지 상태를 더 살펴봐야할까?
dp[2][N-1] 은 현재 N-1번째 줄에서 선택하지 않은 행동에 대해서 얻은 최댓값이라고 정의를 했다. 그렇다면 우린 직관적으로 dp[2][N-1] 는 dp[0][N-1], dp[1][N-1] 보다 계속 작다는 것을 알 수 있다.
일단, dp[0][N-1], dp[1][N-1]에 대해서 현재 스티커 값 cost[0][N-1] cost[1][N-1] 이 추가 되기 때문에 값이 지속적으로 작다.
즉, 상태 2 에 대한 업데이트는 아래와 같이 수정 할 수 있다.
dp[2][N] = max(dp[0][N-1], dp[1][N-1])
해당 사항은 선택적이고, 어떻게 생각해도 상관없다.
앞서서 구현해본 두가지 방식으로 구현해보자.
1) Bottom - Up (Tabulation)
#include<bits/stdc++.h>
using namespace std;
int t;
int s[2][101010];
int n;
int dp[3][101010];
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
fill(&dp[0][0], &dp[2][101010] , 0);
for (int i = 0; i < 2; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &s[i][j]);
}
}
dp[0][0] = s[0][0];
dp[1][0] = s[1][0];
dp[2][0] = 0;
for (int i = 1; i <= n; i++) {
dp[0][i] = max(dp[1][i - 1], dp[2][i - 1]) + s[0][i];
dp[1][i] = max(dp[0][i - 1], dp[2][i - 1]) + s[1][i];
dp[2][i] = max(dp[0][i - 1], max(dp[1][i - 1], dp[2][i - 1]));
}
printf("%d\n", max(dp[0][n - 1], max(dp[1][n - 1], dp[2][n - 1])));
}
return 0;
}2) Top-Down
Top - Down 으로 구현하기 위해서는 DP의 정의를 조금 바꿔야한다.
이렇게 생각해보는건 어떨까? 스티커를 제거하는데 맨 오른쪽에서부터 살펴보자. 즉, cost(int i, int j) 에서 j 는 Bottom-up 과 마찬가지로 상태를 정의하고, 해당 함수는 i번째 열부터에서만 스티커를 제거하여 얻을 수 있는 최대 가치를 구한다는 문제로 바뀐다.
즉 이번에 Base Case는 i == N 일 때로 바뀐다. (N-1번째 열까지만 존재하므로)
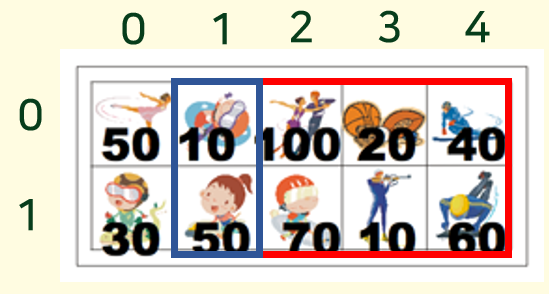
파란색 사각형 : cost(0,1) cost(1,1) cost (2,1) 호출시점
위에 그림에서 살펴보면 현재 cost(0,1)은 2번째~4번째(N-1번째 열) 까지 상태 j 에 따른 최댓값으로 볼 수 있다. Bottom up은 왼쪽에서부터 점화식을 작성한데에 비해서 Top-Down은 끝이 N번째 열이라고 가정하고 끝에서부터 정답을 찾아가는 방식이다.
식을 업데이트 하는 과정은 아래와 같다.
Bottom-up 방식과 마찬가지로, 상태 j는 0은 위에를 뜯었을 경우, 1은 아래를 뜯었을 경우, 2는 전부 뜯지 않았을 경우로 가정했다.
#include<bits/stdc++.h>
using namespace std;
int t;
int s[2][101010];
int n;
int dp[3][101010];
int cost(int i, int j) {
if (j == n) return 0;
else {
if (dp[i][j] != -1) {
return dp[i][j];
}
else {
int cur_cost = -1;
// rip out top
if (i == 0) {
cur_cost = max(cost(2,j+1), cost(1, j+1) + s[0][j]);
}
// rip out bottom
else if (i == 1) {
cur_cost = max(cost(2, j + 1), cost(0, j + 1) + s[1][j]);
}
// Don't rip out anything
else if (i == 2) {
cur_cost = max(cost(2, j + 1),
max(cost(1, j + 1) + s[0][j],
cost(0, j + 1) + s[1][j]));
}
dp[i][j] = cur_cost;
return dp[i][j];
}
}
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
fill(&dp[0][0], &dp[2][101010], -1);
for (int i = 0; i < 2; i++) {
for (int j = 0; j < n; j++) {
scanf("%d", &s[i][j]);
}
}
printf("%d\n", max(cost(0,0), max(cost(1,0),cost(2,0))));
}
return 0;
}사실 관점 차이지만, 재귀적인 방식이라는 점에서만 차이가 있다. 두가지 방식모두 알아 두는 것이 좋을 것 같다.
점화식 2
코드리뷰를 같이 진행하다보니 신기한 점화식이 존재했다.
바로 i-1 번째 식과 i-2 번째 식을 활용하여 dp 값을 업데이트하는 건데 대략적인 방향성은 이렇다.
1) 현재 위쪽 스티커를 제거하기 위해서는 지금까지 대각선으로 제거하거나 (바로전칸 아래 제거), 두열 전에서 아래스티커를 제거하는 것 두경우 밖에 없다.
dp[0][i] = max(dp[1][i-1] , dp[1][i-2]) + cost[0][i]
dp[1][i] = max(dp[0][i-1], dp[1][i-1]) + cost[1][i]
두열전에서 위 스티커를 제거하는 경우는 대각선 경로로 제거하는 것과 동일한 경로이기때문에 겹치는 경우이다.
해당 점화식 또한 점화식 1과 같다는 것을 직관적으로 알 수 있다.
두열전에서 제거했다는 것은 바로 점화식1에서 상태2에 해당한다. 상태2를 잘 살펴본다면 우리는 바로직전의 최댓값에만 영향을 미친다는 것을 알 수 있고, 해당 수식에서 대각선으로 이동한것은 dp[2][N-1] 에서 최댓값을 이동시킨것이라는 것을 알 수 있다.
따라서, 해당 경우에서 관점 차이에 따라 같은 점화식을 수식적인 차이로 다양한 Dynamic Programming 점화식을 세울 수 있다는 것을 알 수 있다.
연습삼아서 간단하게 DP 문제를 Top-Down Bottom-Up 두가지 방식으로 풀어보는게 은근 DP적인 사고를 확장하는데 큰 도움이 될 것 같다. 다음 포스터는 LIS, LCS 조금 더 응용적인 사고방식이 필요한 DP 문제들을 다뤄보면 좋을 것 같다.
Reference
1) Dynamic Programming vs Divide-And-Conquer
https://trekhleb.dev/blog/2018/dynamic-programming-vs-divide-and-conquer/

DP라니.. 안성맞춤 포스팅..!