🔗강의 영상

목차

• process sequences
• RNN
• LSTM (Long Short Term Memory)

process sequences 종류

Vanlilla Neural Networks의 한계는 고정된 크기의 vector를 입력으로 받아들이고 고정 크기의 vector를 출력한다는 점이다. RNN은 vector sequence에 대해 연산을 수행한다. RNN은 아래와 같은 가변적인 데이터에 효과적이다.

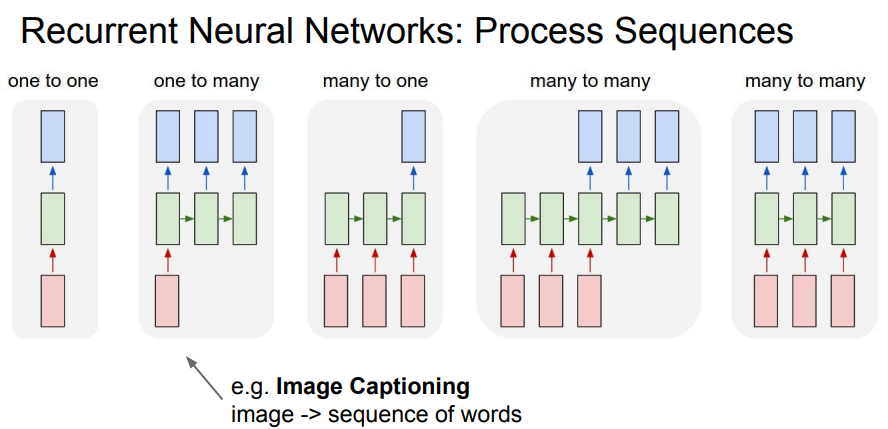
빨강 box: input vector, 파랑: output vector, 녹색: RNN state

• one to one: 일반적인 경우
• one to many: image captioning(한 사진에서 여러 라벨을 뽑아내는 것)
• many to one: sentiment classification (감정 분류)
• many to many: 기계 번역, 비디오 분류 (비디오는 여러 프레임의 사진으로 이루어져있음)

RNN의 동작 원리

input x가 rnn에 입력된다. rnn은 hidden state를 가진다. hidden state는 rnn에 새로운 입력이 들어올 때마다 업데이트 된다. 업데이트 된 hidden state는 모델에 피드백 되고, 이후에 또 다른 입력 x가 들어온다.

활성화 함수: tanh. 값 범위: -1<=x<=1

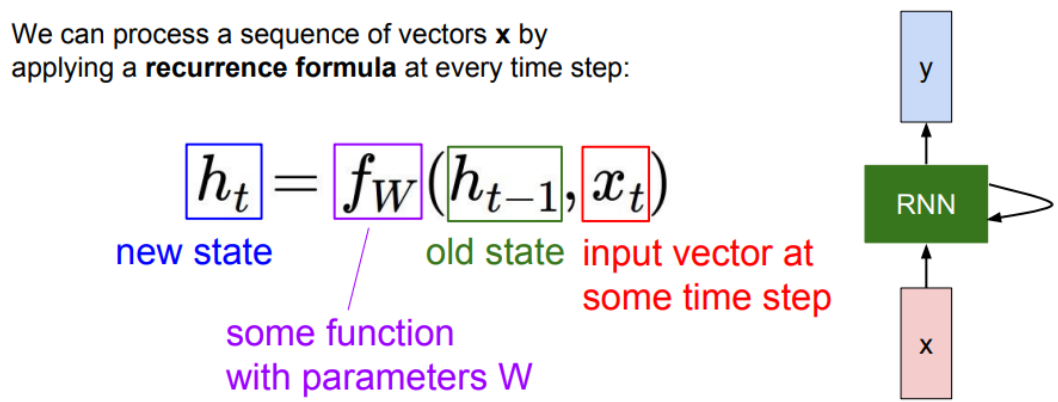
Sequence vectore xt를 받는다. hidden state를 업데이트한다. 출력값을 내보낸다.

character-level language model example - 다음 알파벳을 예측하는 rnn 모델 예시 코드
https://gist.github.com/karpathy/d4dee566867f8291f086

Minimal character-level language model with a Vanilla Recurrent Neural Network, in Python/numpy

rnn 활용 기술 ‘Image Captioning’

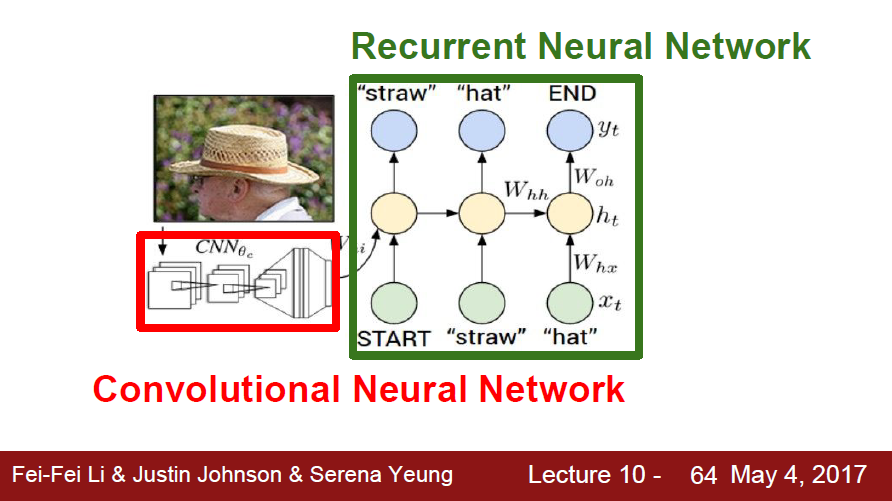
구조

• Cnn: 이미지 처리해서 고차원 벡터(이미지의 주요 특징) 출력
• RNN: cnn 결과를 입력되어 이미지 정보를 기억하고 단어를 예측

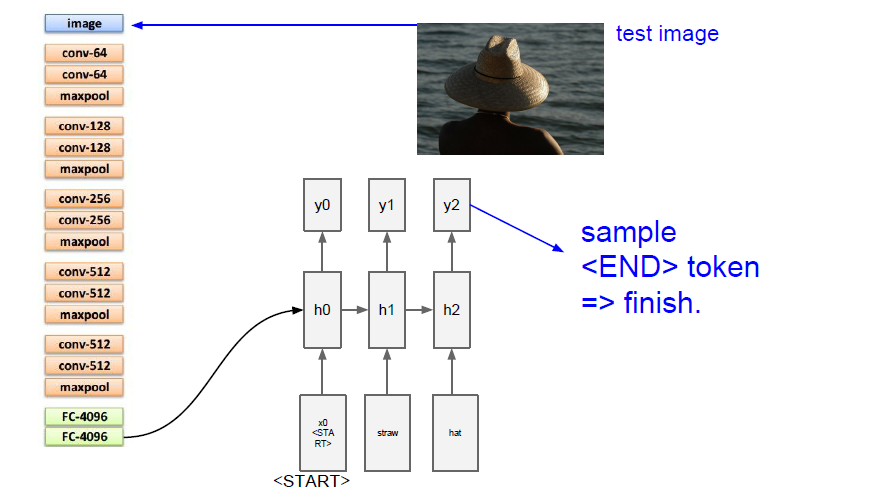
사용 예시 데이터셋: Microsoft - COCO

image captioning은 지도학습이라 큰 데이터셋이 필요하다. 대표적인 데이터셋은 microsoft의 coco이다. 코코는 328,000개의 이미지가 있고, 2,500,000개의 라벨이 지정된 인스턴스가 있다.

코코 데이터셋으로 이미지 캡셔닝 학습시킨 후 이미지를 입력하여 캡션 데이터를 출력한 결과.

RNN의 단점

장기 의존성(Long-term dependencies) 문제

• 장기 의존성: 길이가 길어질수록 첫 부분의 정보를 잃어버리는 현상

LSTM (Long Short Term Memory)

rnn은 장기 의존성 문제 때문에 실제로 현업에서 사용하기엔 한계가 있다. 현업에서 rnn대신 lstm을 더 많이 사용한다.

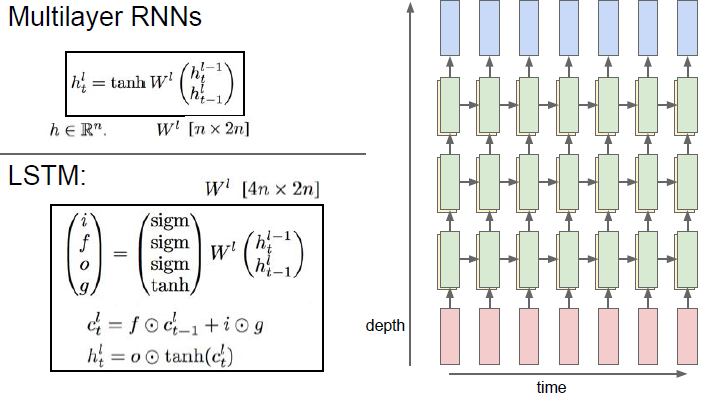
초록색: hidden state, 노란색: cell state. cell state는 왼쪽 아래와 같은 수식을 통과한다

lstm 구조 (Cell state)

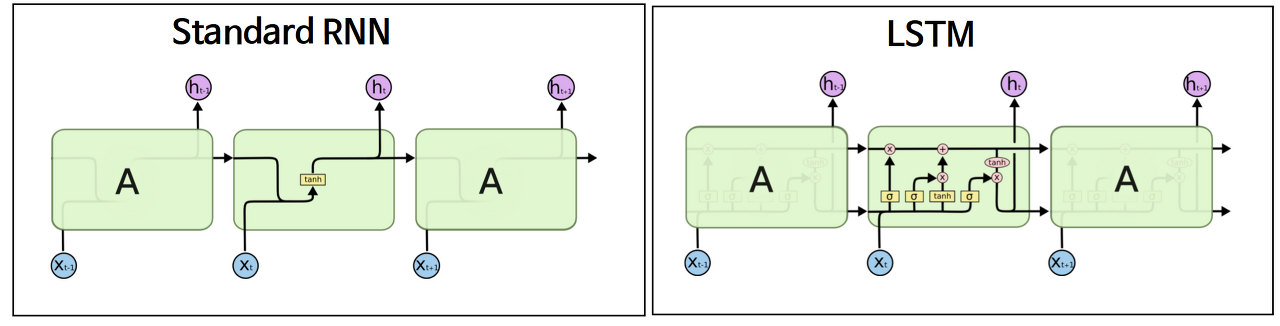
cell state란

lstm 모델 구조도에서 cell state는 수평선처럼 표현되는 정보의 흐름을 말한다.

개념

LSTM도 기본 RNN과 같이 체인처럼 이어져 있는(chain-like) 모양이지만, lstm에서는 cell state라는 새로운 구조적 개념이 사용된다.
cell state는 LSTM의 이전 상태에서 현재 상태까지 유지되는 정보의 흐름을 말한다.

cell state 구조의 이점

오래된 정보를 기억하고 새로운 정보를 적절하게 갱신할 수 있다. 즉, 장기 의존성 문제를 해결할 수 있다.

구조, update 과정

• 입력: 이전 hidden state를 쌓아둔 것.
• 입력에 4개의 gates 값을 계산하기 위해 커다란 가중치 행렬을 곱한다.

gate

정보를 선택적으로 통과시키는 길.
sigmoid 네트워크 층과 접곱(point wise multiplication) 연산으로 이루어진다.

• 접곱: 같은 크기의 두 벡터나 행렬의 동일한 위치에 있는 원소들끼리 곱하는 연산.
  예를 들어 두 벡터 A = [a1, a2, a3]와 B = [b1, b2, b3]가 있을 때, A와 B의 접곱: [a1b1, a2b2, a3*b3]

cell state에는 input gate, forget gate, 새로운 cell state 생성 또는 업데이트 (딱히 gate 관련한 지칭이 존재하지 않음), output gate로 총 4개의 gate가 존재한다.

i (input gate)

cell state에 어떤 정보를 추가할지 결정한다. xt(현재 input)와 ht-1(이전 hidden state)를 입력으로 받아 sigmoid 함수를 통과시킨다.

f (forget gate)

cell state에서 어떤 정보를 망각할지(버릴지) 결정한다. xt와 ht-1를 받아 sigmoid 함수를 통과시킨다. 0~1사이의 값을 가지는데 0 이전 정보를 내보내지 않고 1이면 이전 정보를 모두 전달한다는 걸 의미한다.

g (새로운 cell state 생성)

앞서 거쳤던 단계에서 결정한 대로 새로운 값을 추가하고, 정보를 망각하여 c_t(새로운 cell state)를 생성한다. tanh함수를 사용하기 때문에 -1~1 사이의 값을 갖는다.

o(output gate)

update된 cell state를 바탕으로 최종 hidden state를 결정한다. xt(현재 input)과 h{t-1}(이전 hidden state)를 받아 sigmoiod 함수에 통과시킨다. 그리고 update된 cell state를 tanh 함수에 통과시킨 후, 이 두 결과를 곱한다.

rnn보다 lstm이 더 좋은 이유

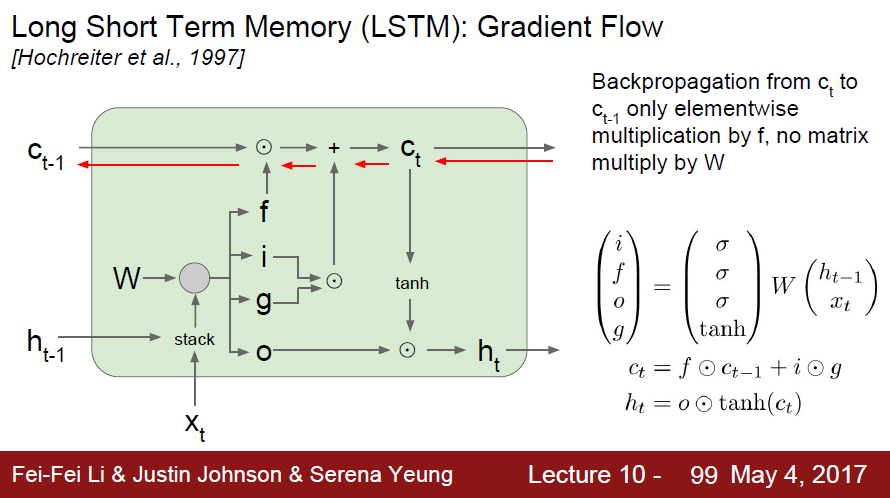
• vanilla RNN은 가중치 행렬 w가 계속해서 곱해지는 문제가 Backward pass에서 발생한다. lstm은 rnn과 다르게 f 연산에서 행렬 전체를 곱(full matrix multiplication)하는 대신 각 요소별로 곱셈(element-wise)이 이루어진다. 매 스텝마다 다른 값의 f와 곱해질 수 있다는 점이 다르다. vanilla RNN의 경우에는 동일한 가중치 행렬(h_t)만을 계속 곱했다. 이는 exploding/vanishing gradient 문제를 일으켰었는데, 반면 LSTM에서는 f가 스텝마다 계속 변해서 gradient 문제가 발생하지 않는다.

• lstm의 cell state 과정에서 f는 sigmoid에서 나온 값이므로 요소 별 행렬 곱 값(element wise multply)이 0~1 사이의 값이다. f를 반복적으로 곱한다고 했을 때 더 좋은 수치적인 특성으로 변한다.

• vanilla RNN의 backward pass에서는 매 스텝에서 gradient가 tanh를 거쳤다. LSTM에서도 hidden state h_t를 출력 y_t를 계산하는데 사용한다. 만약 LSTM의 h_t(최종 hidden state)를 가장 첫 cell state(c_0)까지 backprop하는 걸 생각해보면, RNN처럼 매 스텝마다 tanh를 거칠 필요가 없다. 단 한 번만 tanh를 거치면 된다.