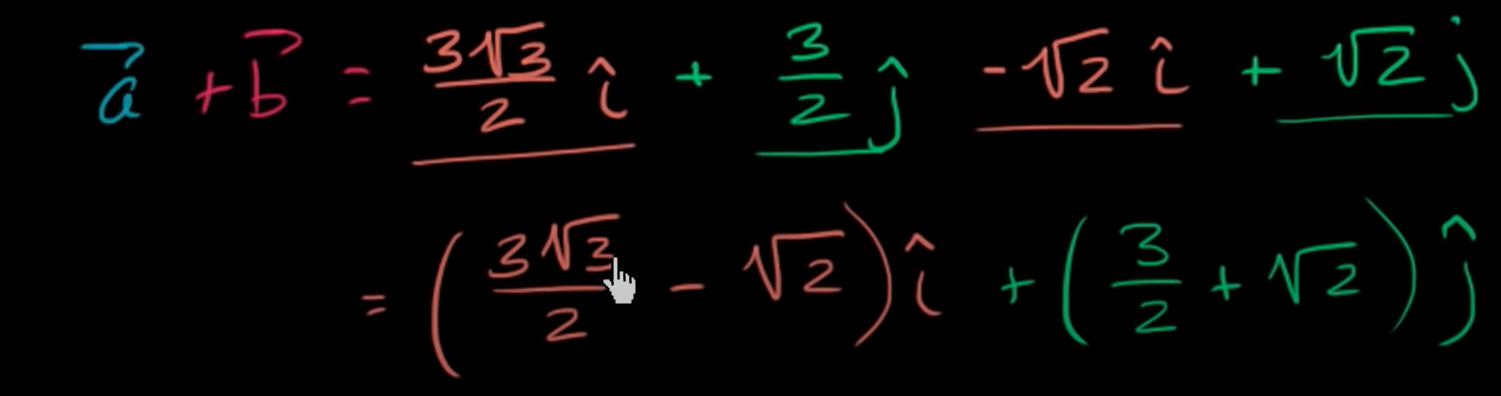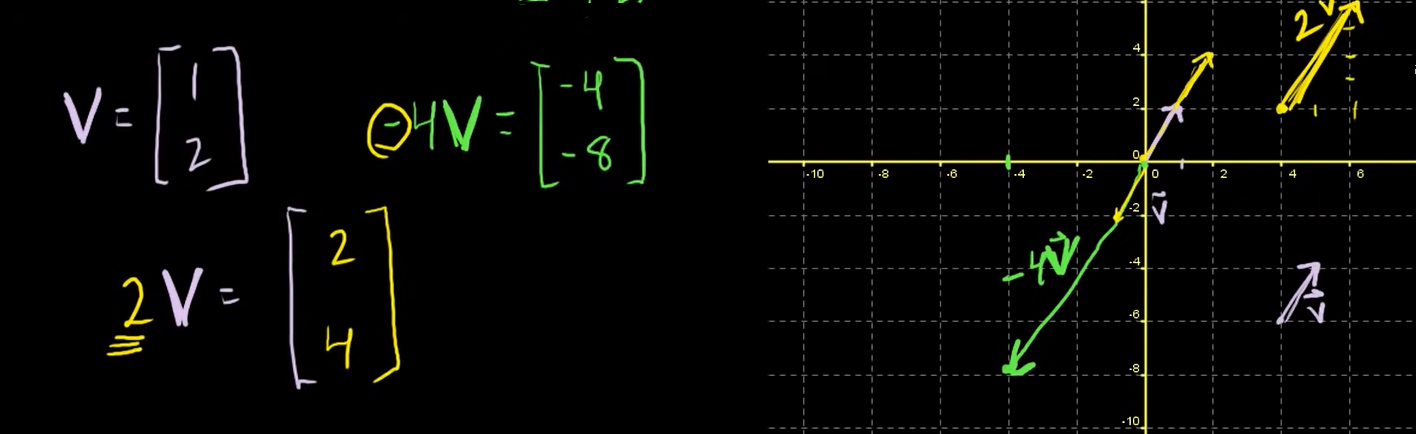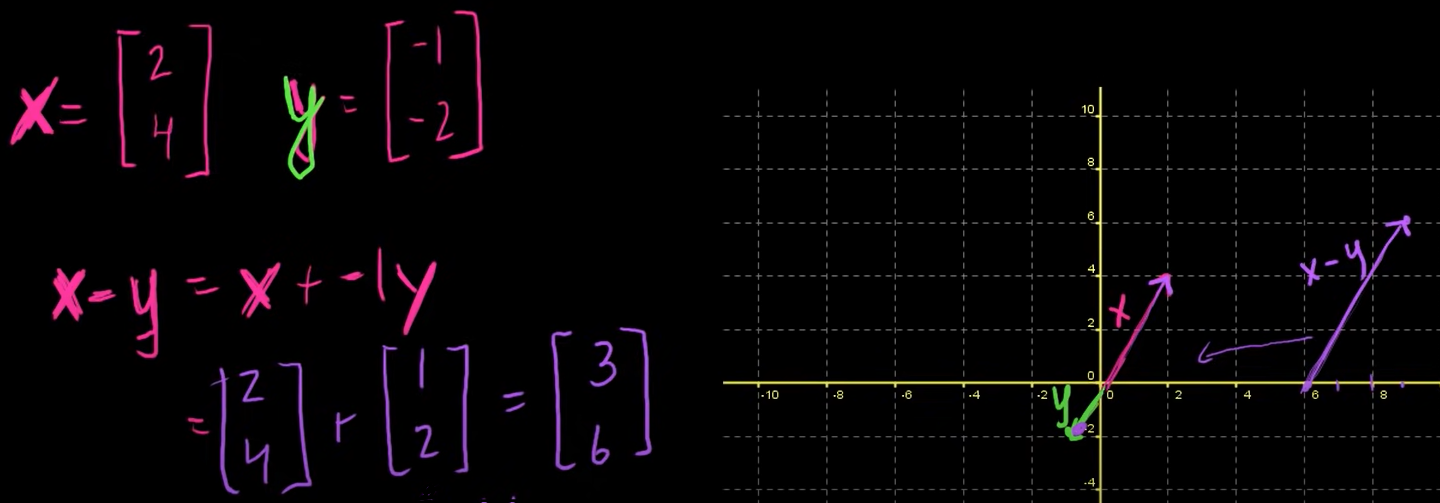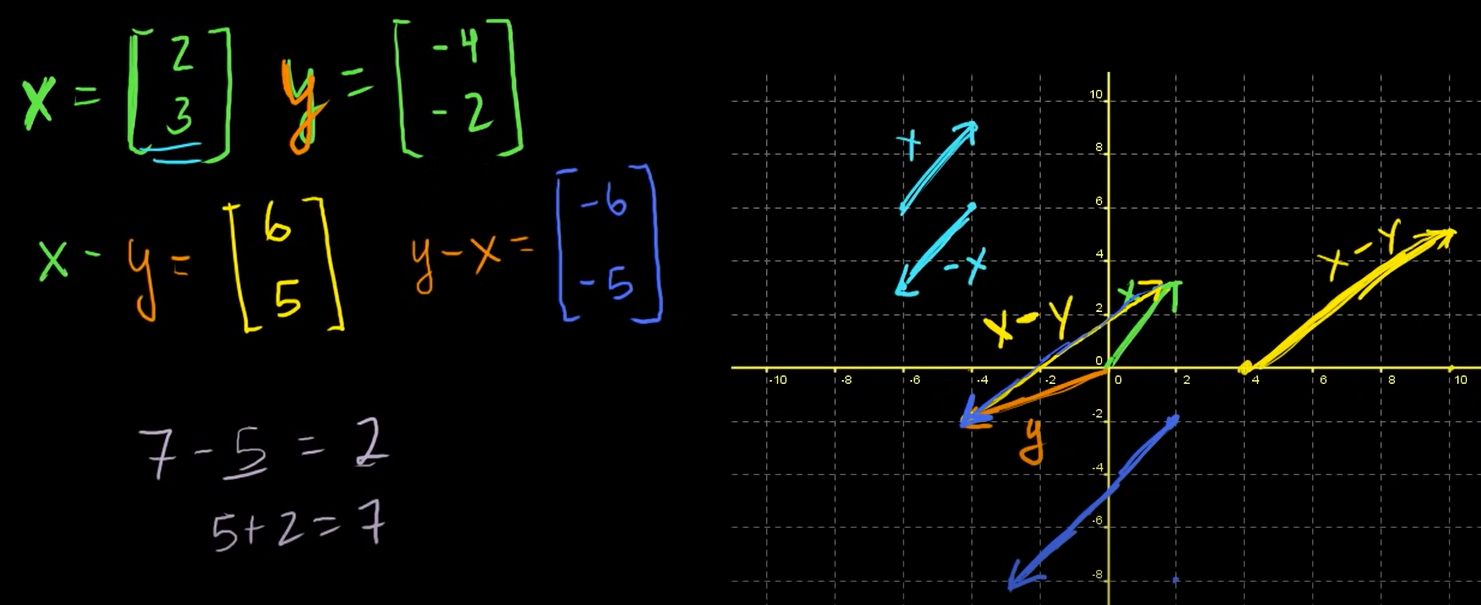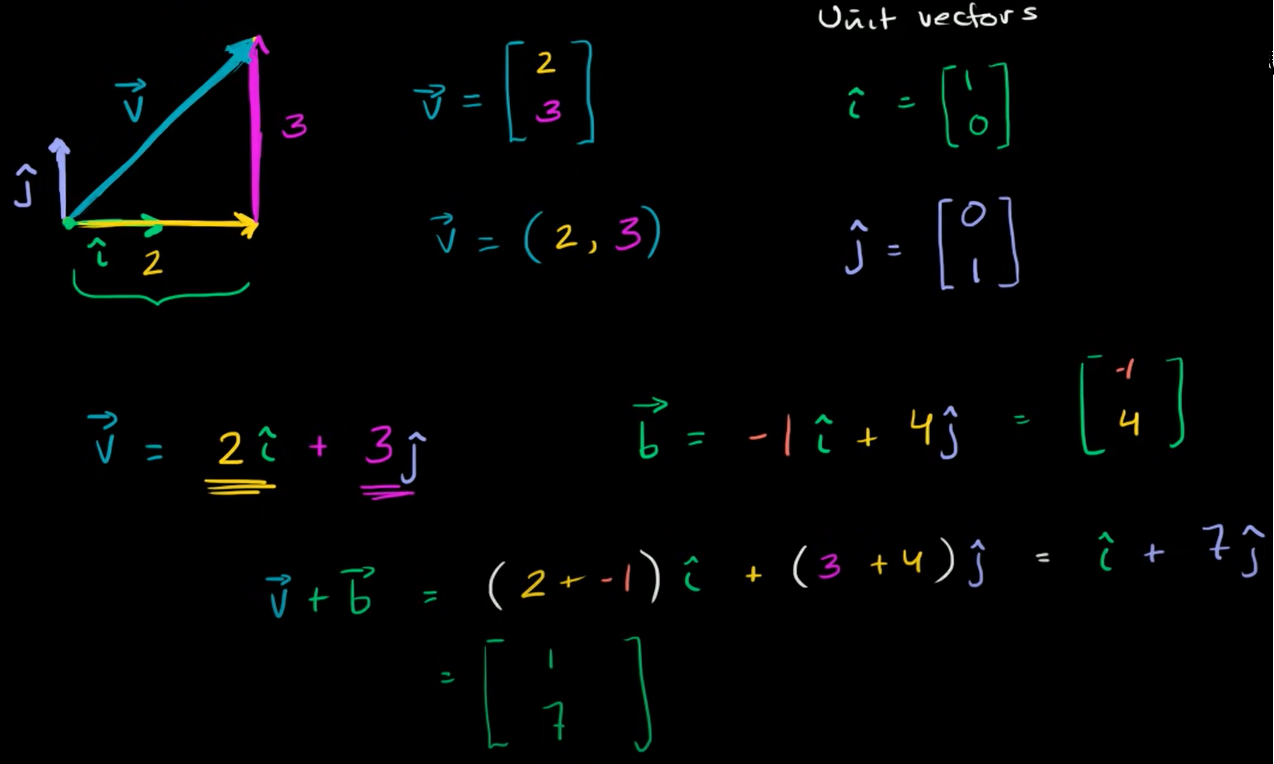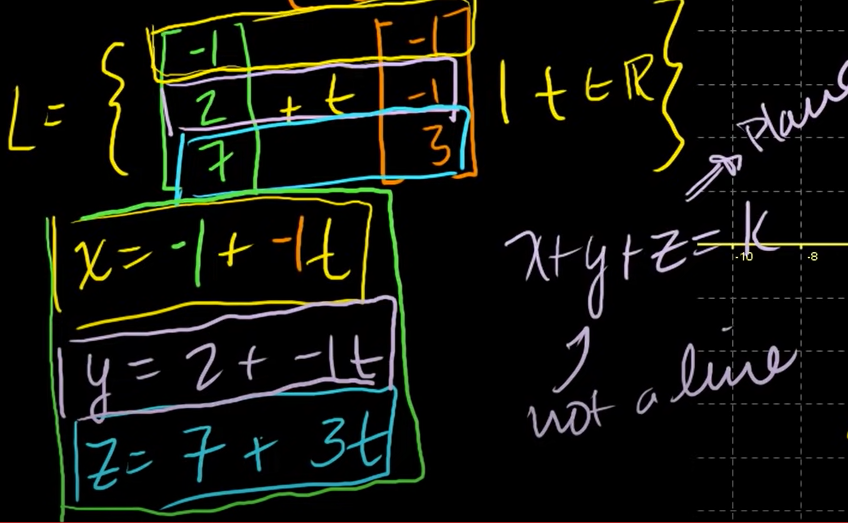1. 벡터(Vector)란?
벡터(vector) = 크기(magnitude) + 방향(direction)
5mph ⇨ 스칼라(scalar)
5mph east ⇨ 속도(velocity) ⇨ 벡터(vector)
특징 : 시작점의 위치는 상관이 없다.
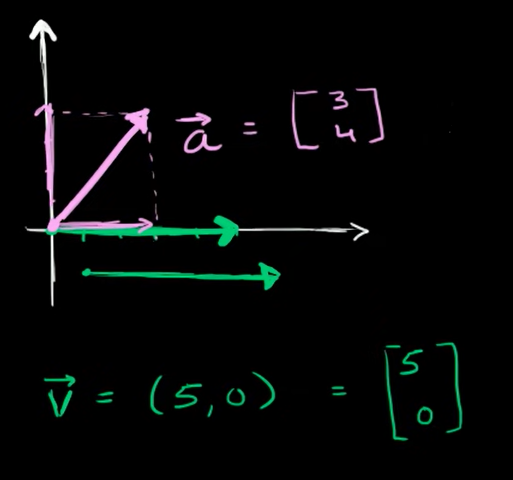
아래 그림에서 a → \overrightarrow{a} a
2. 실좌표 공간
R 2 = R 2 \mathbb{R^2} = \mathbf{R^2} R 2 = R 2
실좌표 공간 Real coordinate space 2-dimensional
실수값을 갖는 2-튜플 = all possible real value 2-tuple
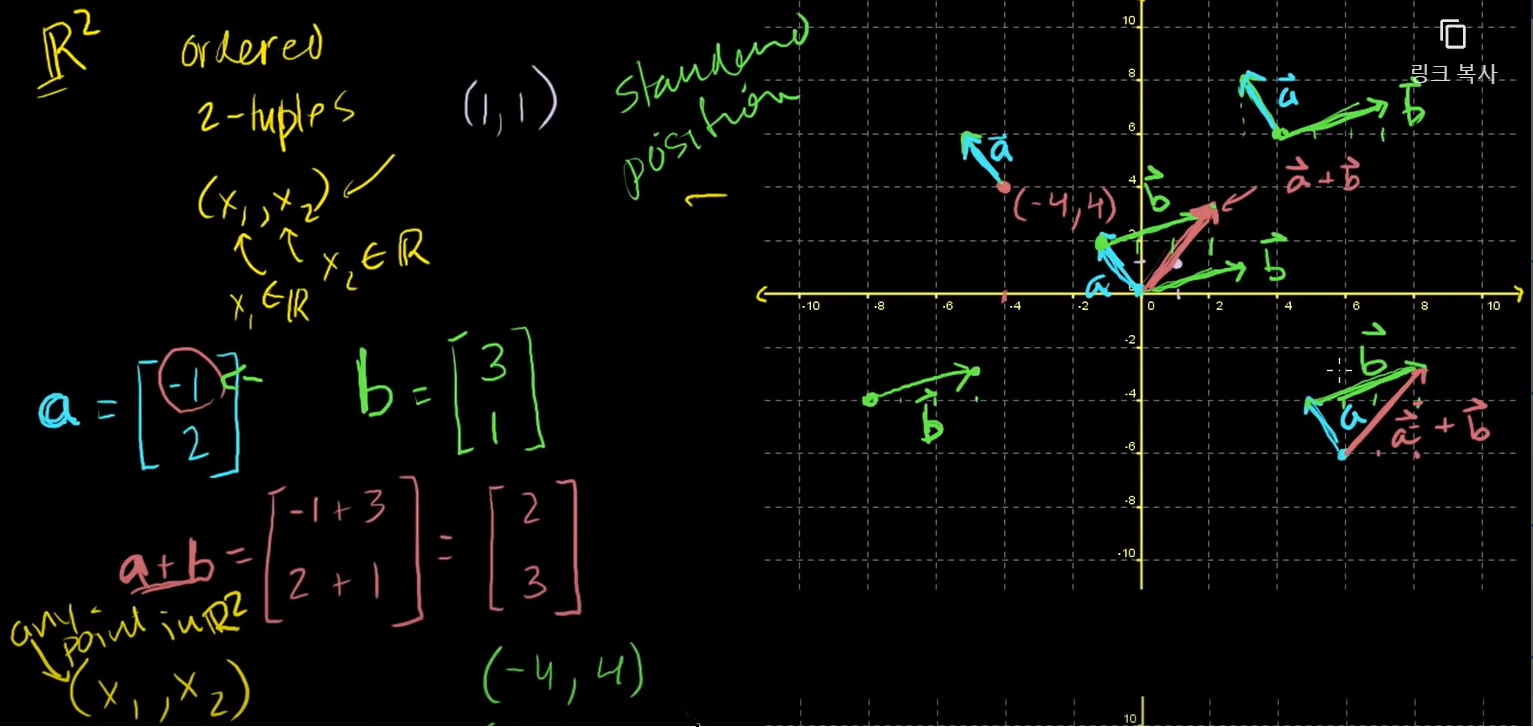
위의 사진이 시각적 표현이라 할 수 있다.
R 3 \mathbb{R^3} R 3
X → = [ 0 0 0 ] , b → = [ − 1 5 3 ] \overrightarrow{X} = \begin{bmatrix} 0\\0\\0 \end{bmatrix}, \overrightarrow{b} = \begin{bmatrix} -1\\5\\3 \end{bmatrix} X = ⎣ ⎢ ⎡ 0 0 0 ⎦ ⎥ ⎤ , b = ⎣ ⎢ ⎡ − 1 5 3 ⎦ ⎥ ⎤
벡터는 X , b X, b X , b R 3 \mathbb{R^3} R 3 X → ∈ R 3 \overrightarrow{X} \in \mathbb{R^3} X ∈ R 3
하지만 c → = [ i 0 1 ] , c → ∉ R 2 \overrightarrow{c} = \begin{bmatrix} i\\0\\1 \end{bmatrix}, \qquad \overrightarrow{c} \notin \mathbb{R^2} c = ⎣ ⎢ ⎡ i 0 1 ⎦ ⎥ ⎤ , c ∈ / R 2 c \qquad c c
R n \mathbb{R^{n}} R n
3. 벡터의 덧셈
a → = [ 6 − 2 ] , b → = [ − 4 4 ] , a → b → ∈ R 2 \overrightarrow{a} = \begin{bmatrix} 6\\-2 \end{bmatrix},\qquad \overrightarrow{b} = \begin{bmatrix} -4\\4 \end{bmatrix}, \qquad \overrightarrow{a}\overrightarrow{b} \in \mathbb{R^2} a = [ 6 − 2 ] , b = [ − 4 4 ] , a b ∈ R 2
a → + b → = [ 6 + ( − 4 ) ( − 2 ) + 4 ] = [ 2 2 ] = b → + a → \overrightarrow{a}+\overrightarrow{b} = \begin{bmatrix} 6+(-4)\\(-2)+4 \end{bmatrix} = \begin{bmatrix} 2\\2 \end{bmatrix} = \overrightarrow{b} + \overrightarrow{a} a + b = [ 6 + ( − 4 ) ( − 2 ) + 4 ] = [ 2 2 ] = b + a
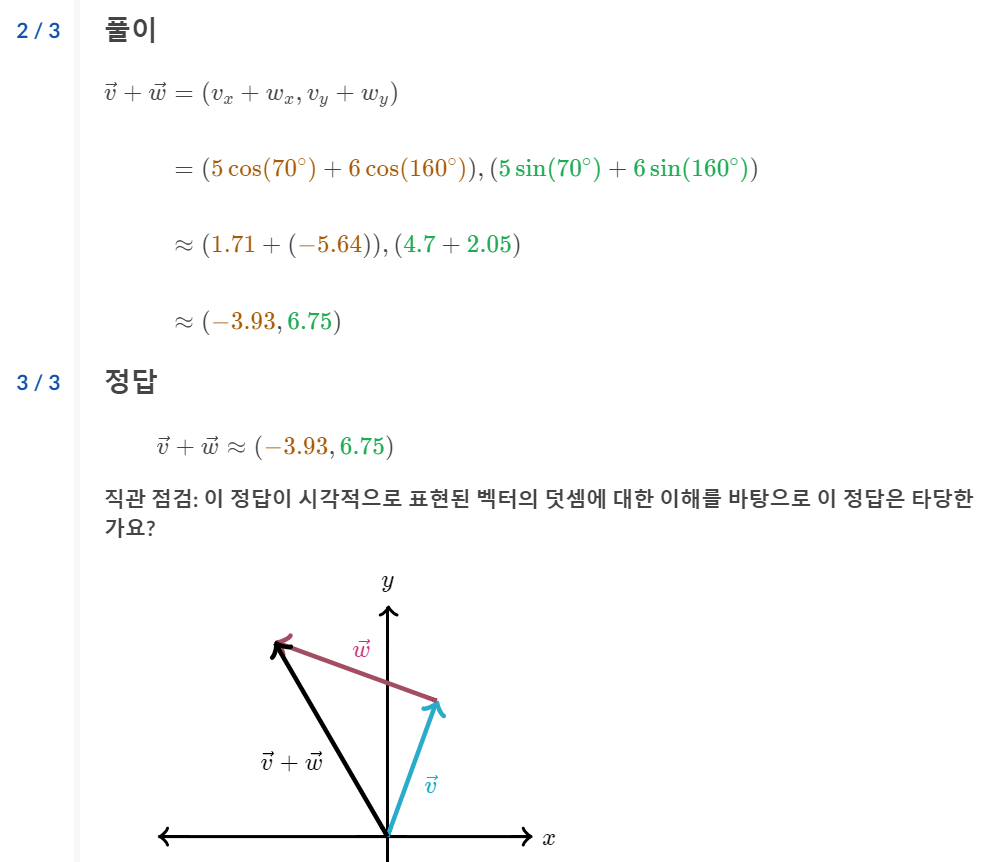
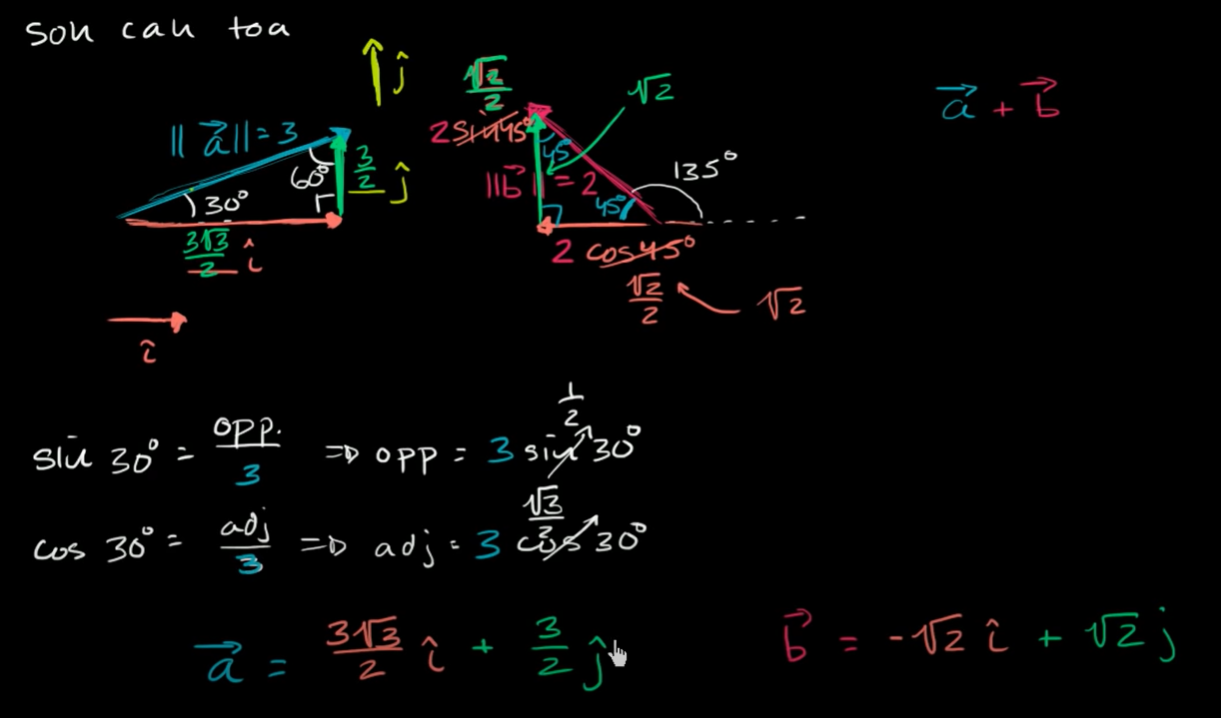
3-1)크기와 방향으로 나타낸 벡터의 덧셈
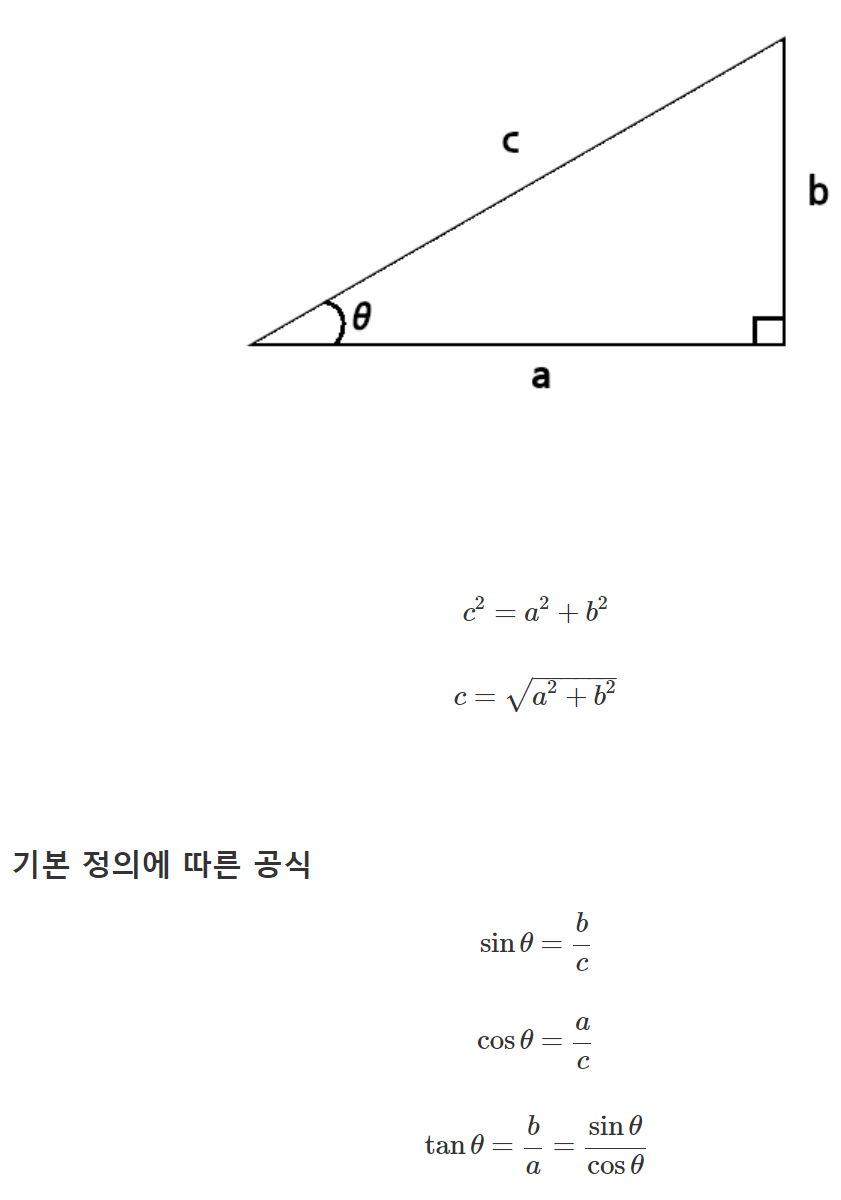
참조 : 삼각함수
4. 벡터와 스칼라의 곱
a → = [ 2 1 ] \overrightarrow{a} = \begin{bmatrix} 2\\1 \end{bmatrix} a = [ 2 1 ]
아래의 사진에서 핑크색 화살표이다.
3 a → = 3 [ 2 1 ] = [ 3 ⋅ 3 3 ⋅ 1 ] = [ 6 3 ] 3\overrightarrow{a} = 3\begin{bmatrix} 2\\1 \end{bmatrix} = \begin{bmatrix} 3 \cdot 3\\3 \cdot 1 \end{bmatrix} = \begin{bmatrix} 6\\3 \end{bmatrix} 3 a = 3 [ 2 1 ] = [ 3 ⋅ 3 3 ⋅ 1 ] = [ 6 3 ]
여기서 3은 스칼라(Scalar)이며 아래의 그림에서는 민트색 화살표이다. 핑크색 화살표와 비교햇을 때 크기만 변하고 방향이 같다(same direction)
− 1 a → = [ 2 ⋅ ( − 1 ) 1 ⋅ ( − 1 ) ] = [ − 2 − 1 ] -1\overrightarrow{a} = \begin{bmatrix} 2 \cdot (-1)\\1 \cdot (-1) \end{bmatrix} = \begin{bmatrix} -2\\-1 \end{bmatrix} − 1 a = [ 2 ⋅ ( − 1 ) 1 ⋅ ( − 1 ) ] = [ − 2 − 1 ]
아래의 그림에서 초록색 화살표. 핑크색과 비교하면 뱡향만 변하고 크기는 그대로이다.
− 2 a → = [ 2 ⋅ ( − 2 ) 1 ⋅ ( − 2 ) ] = [ − 4 − 2 ] -2\overrightarrow{a} = \begin{bmatrix} 2 \cdot (-2)\\1 \cdot (-2) \end{bmatrix} = \begin{bmatrix} -4\\-2 \end{bmatrix} − 2 a = [ 2 ⋅ ( − 2 ) 1 ⋅ ( − 2 ) ] = [ − 4 − 2 ]
아래의 그림에서 주황색 화설표. 핑크와 비교하면 크기, 방향 모두 바뀌었다.
5. 벡터 예제
벡터의 덧셈
standard position 표준시작점 : (0, 0)을 벡터 시작점으로 잡음
(x 1 , x 2 x_{1}, x_{2} x 1 , x 2 R 2 \mathbb{R^2} R 2
스칼라와 벡터의 곱
종합
일반화
R 4 a = [ 0 − 1 2 3 ] b = [ 4 − 2 0 5 ] \mathbb{R^4} \qquad a=\begin{bmatrix} 0\\-1\\2\\3 \end{bmatrix}\qquad b=\begin{bmatrix} 4\\-2\\0\\5 \end{bmatrix} R 4 a = ⎣ ⎢ ⎢ ⎢ ⎡ 0 − 1 2 3 ⎦ ⎥ ⎥ ⎥ ⎤ b = ⎣ ⎢ ⎢ ⎢ ⎡ 4 − 2 0 5 ⎦ ⎥ ⎥ ⎥ ⎤
4 a − 2 b = 4 [ 0 − 1 2 3 ] − 2 [ 4 − 2 0 5 ] = [ 0 − 4 8 12 ] − [ 8 − 4 0 10 ] = [ − 8 0 8 2 ] 4a- 2b = 4\begin{bmatrix} 0\\-1\\2\\3 \end{bmatrix}-2\begin{bmatrix} 4\\-2\\0\\5 \end{bmatrix} = \begin{bmatrix} 0\\-4\\8\\12 \end{bmatrix}-\begin{bmatrix} 8\\-4\\0\\10 \end{bmatrix} = \begin{bmatrix} -8\\0\\8\\2 \end{bmatrix} 4 a − 2 b = 4 ⎣ ⎢ ⎢ ⎢ ⎡ 0 − 1 2 3 ⎦ ⎥ ⎥ ⎥ ⎤ − 2 ⎣ ⎢ ⎢ ⎢ ⎡ 4 − 2 0 5 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ 0 − 4 8 1 2 ⎦ ⎥ ⎥ ⎥ ⎤ − ⎣ ⎢ ⎢ ⎢ ⎡ 8 − 4 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ − 8 0 8 2 ⎦ ⎥ ⎥ ⎥ ⎤
6. 단위 벡터(Unit Vector)
2-tuple을 다르게 표현하는 방법
단위 벡터는 오로지 한방향으로만 갈 수 있음(아래그램 참조)
i ^ \hat{i} i ^ j ^ \hat{j} j ^
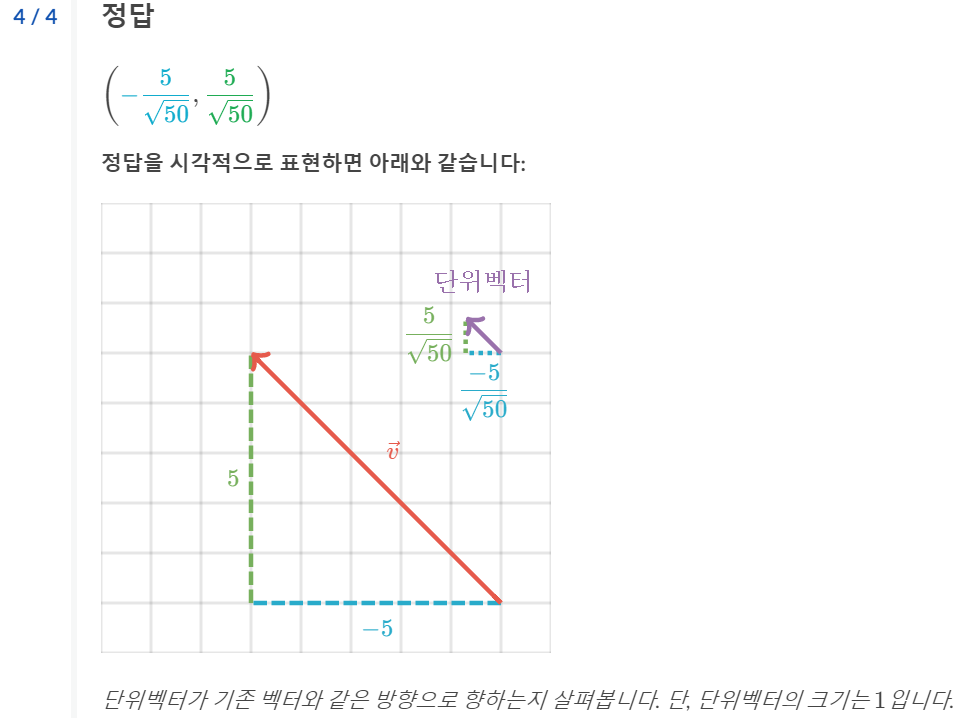
단위벡터 구하는 공식
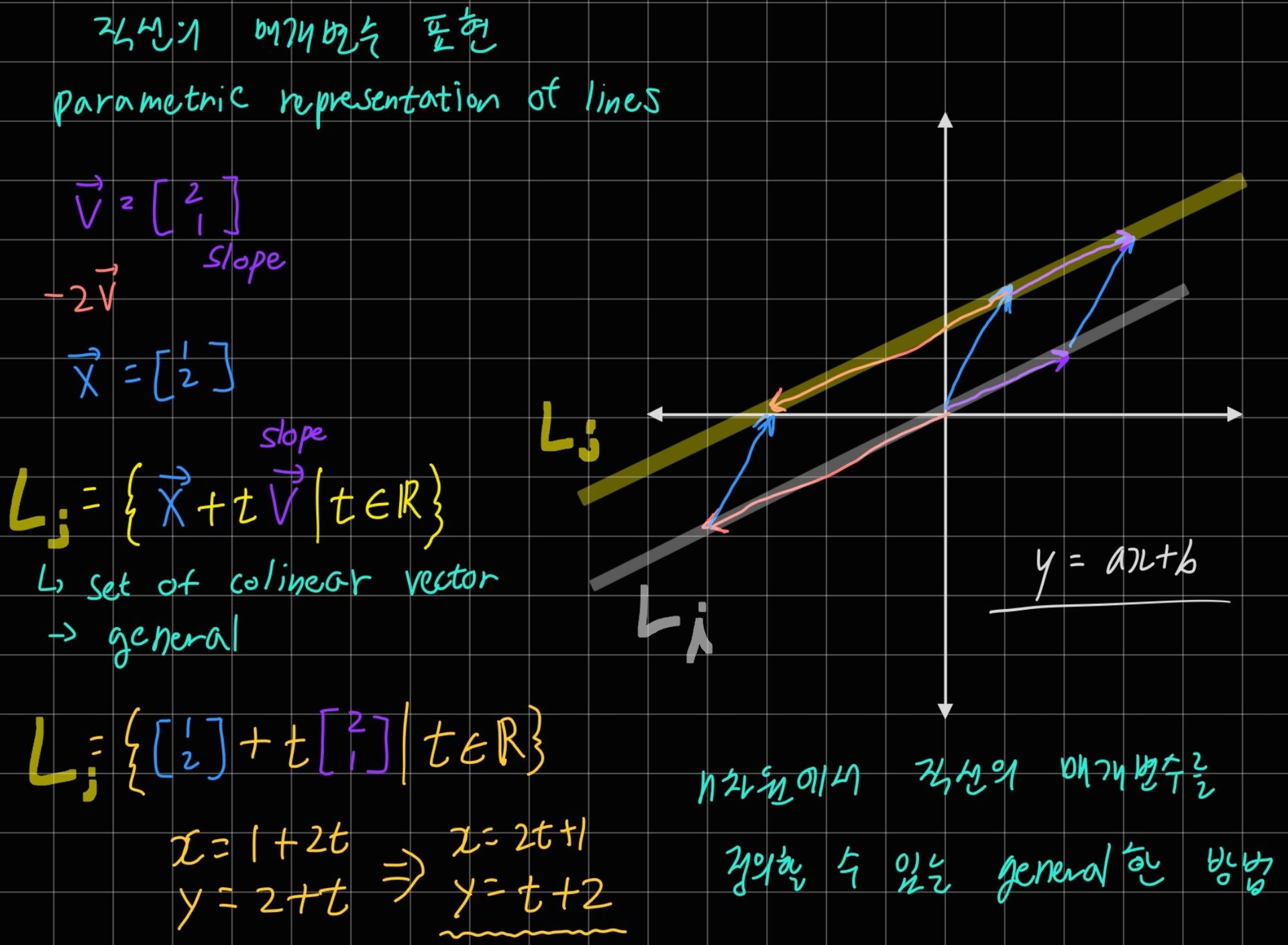
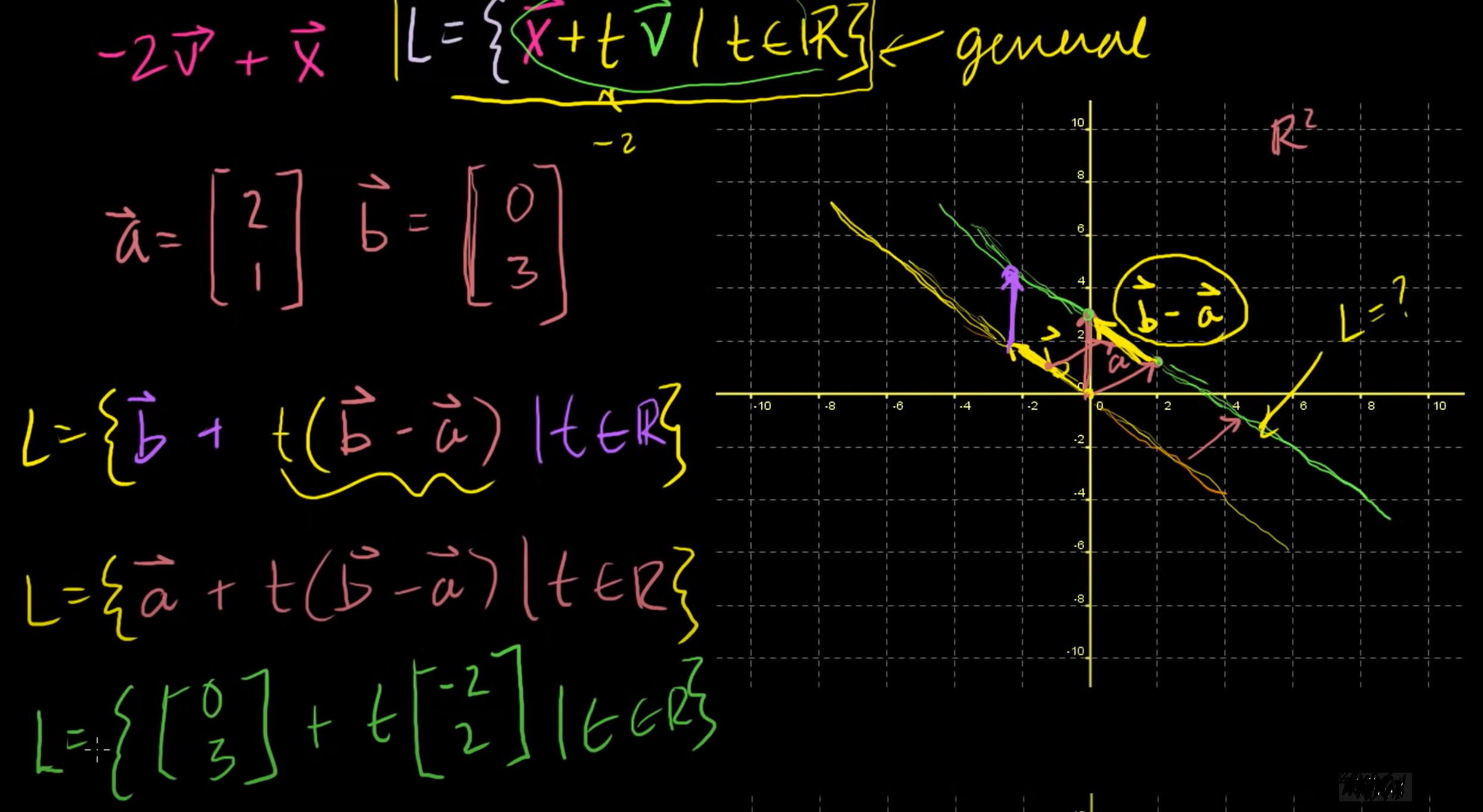
7. 직선의 매개변수