별 모양 다각형 그리기
각도를 이용한 그리기
https://velog.io/@uuranus/Android-%EB%B3%84-%EA%B7%B8%EB%A6%AC%EA%B8%B0-with-Jetpack-Compose
이전 포스팅을 참고해주세요
꼭짓점 둥글게 하기
각도 구하기
꼭짓점을 둥글게 하기 위해서는 우선 둥글게 하는 원의 접점을 알아야한다.
그래야 그 부분부터 원을 그려서 둥글게 할 수 있다.
그리고 접점을 알고 싶으면 다음과 같이 꼭짓점의 각도를 구해야 한다.
별 모양을 십각형이라고 생각하고 내각을 구하는 공식을 이용하면 안쪽 꼭짓점 각도와 바깥쪽 꼭짓점 각도를 구할 수 있다.
위처럼 ϴ'은 정다각형의 내각 구하는 공식으로 구할 수 있고 2*a + ϴ = ϴ' 이고 ϴ' + a = 180도 라는 식을 이용하면 ϴ와 ϴ'을 구할 수 있다.
val totalPoints = numOfPoints * 2
val innerPointAngleDegree = (totalPoints - 2) * 180f / totalPoints
val outerPointAngleDegree =
innerPointAngleDegree - (360f - innerPointAngleDegree * 2)접점 구하기
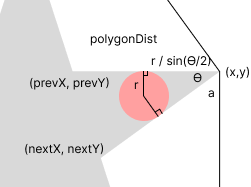
원의 중심좌표를 모르기 때문에 꼭짓점의 좌표값들과 길이의 값을 토대로 점접의 위치를 구하기로 하였다.
val dx = vertices[1].first - vertices[0].first
val dy = vertices[1].second - vertices[0].second
val polygonDist = sqrt(dx * dx + dy * dy)
val circleTangentDist = curCornerRadius / tan((curPointAngleDegree / 2f).toRadian())
val tangentRatio = circleTangentDist / polygonDist
val anchor1 = Pair(
prevX + (x - prevX) * (1 - tangentRatio),
prevY + (y - prevY) * (1 - tangentRatio)
)
val anchor2 = Pair(
x + (nextX - x) * (tangentRatio),
y + (nextY - y) * (tangentRatio)
)원의 중심 좌표 구하기
원래는 접점좌표를 구했던 것처럼 비율로 구할려고 했었다.
그러나 오차 때문인지 실제 중심좌표와는 다른 값이 계산이 되어서 접점의 좌표를 토대로 중심좌표를 구하는 방식으로 변경하였다.
var middleX =
((nextX - x) / (nextY - y)) * anchor2.first + anchor2.second -
((x - prevX) / (y - prevY)) * anchor1.first - anchor1.second
middleX /=
((nextX - x) / (nextY - y) - (x - prevX) / (y - prevY))
val middleY =
-((x - prevX) / (y - prevY)) * middleX +
((x - prevX) / (y - prevY)) * anchor1.first + anchor1.second
val circleCenter = Pair(
middleX,
middleY
)중심좌표 구하는 식은 GPT한테 물어봤다.
이렇게 중심좌표와 점접을 구해서 찍어보면
다음처럼 직각으로 잘 잘리는 걸 볼 수 있다.
회전 각도 구하기
arcTo로 원을 그리려면 시작 각도와 회전할 각도를 구해야한다.
회전각도는 180도 - 위에서 구한 꼭짓점 각도를 하면 되며
시작 각도는 anchor1의 좌표와 원 중심 좌표를 이용해 atan2를 이용하여 각도를 구했다.
회전 각도는 마찬가지로 anchor2과 중심좌표와의 각도를 구하고 시작 각도와 빼주었다.
val startAngleDegree = atan2(
anchor1.second.toDouble() - circleCenter.second.toDouble(),
anchor1.first.toDouble() - circleCenter.first.toDouble()
).toFloat().toDegree()
val endAngleDegree = atan2(
anchor2.second.toDouble() - circleCenter.second.toDouble(),
anchor2.first.toDouble() - circleCenter.first.toDouble()
).toFloat().toDegree()
var sweepAngle = if (endAngleDegree < startAngleDegree) {
startAngleDegree - endAngleDegree
} else {
endAngleDegree - startAngleDegree
}
if (sweepAngle > 180f) {
sweepAngle = 360f - sweepAngle
}그리고 원을 구해보면
이렇게 꼭짓점의 개수가 작을 때는 잘 되는데
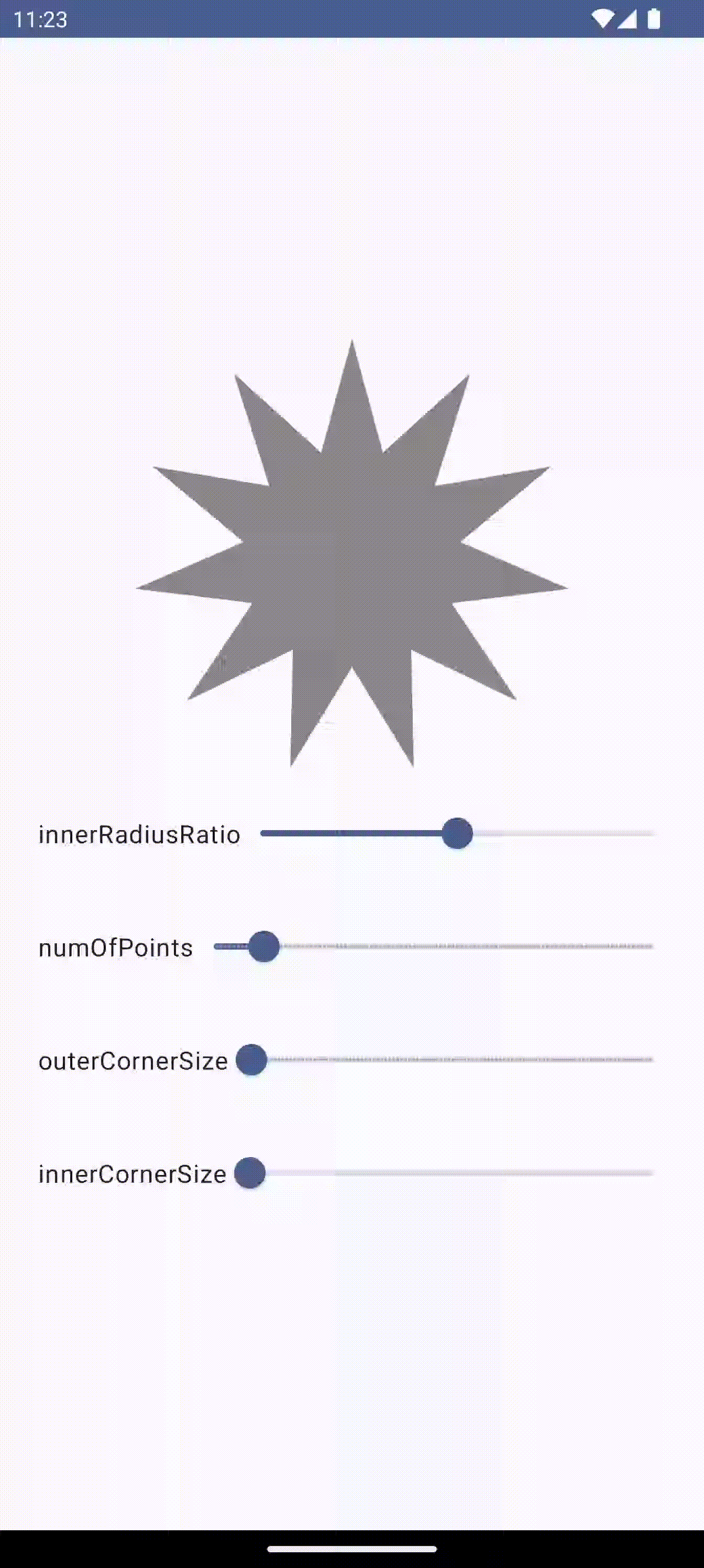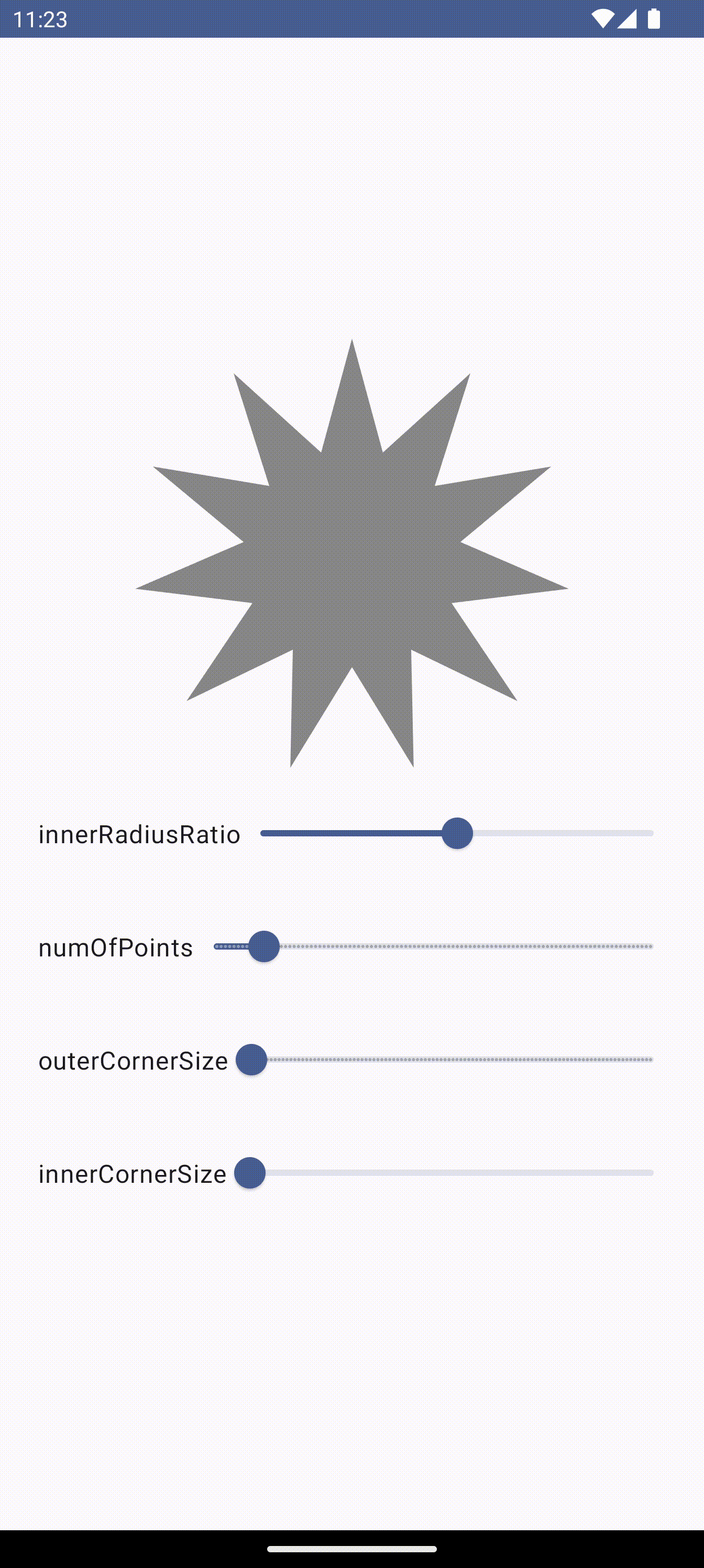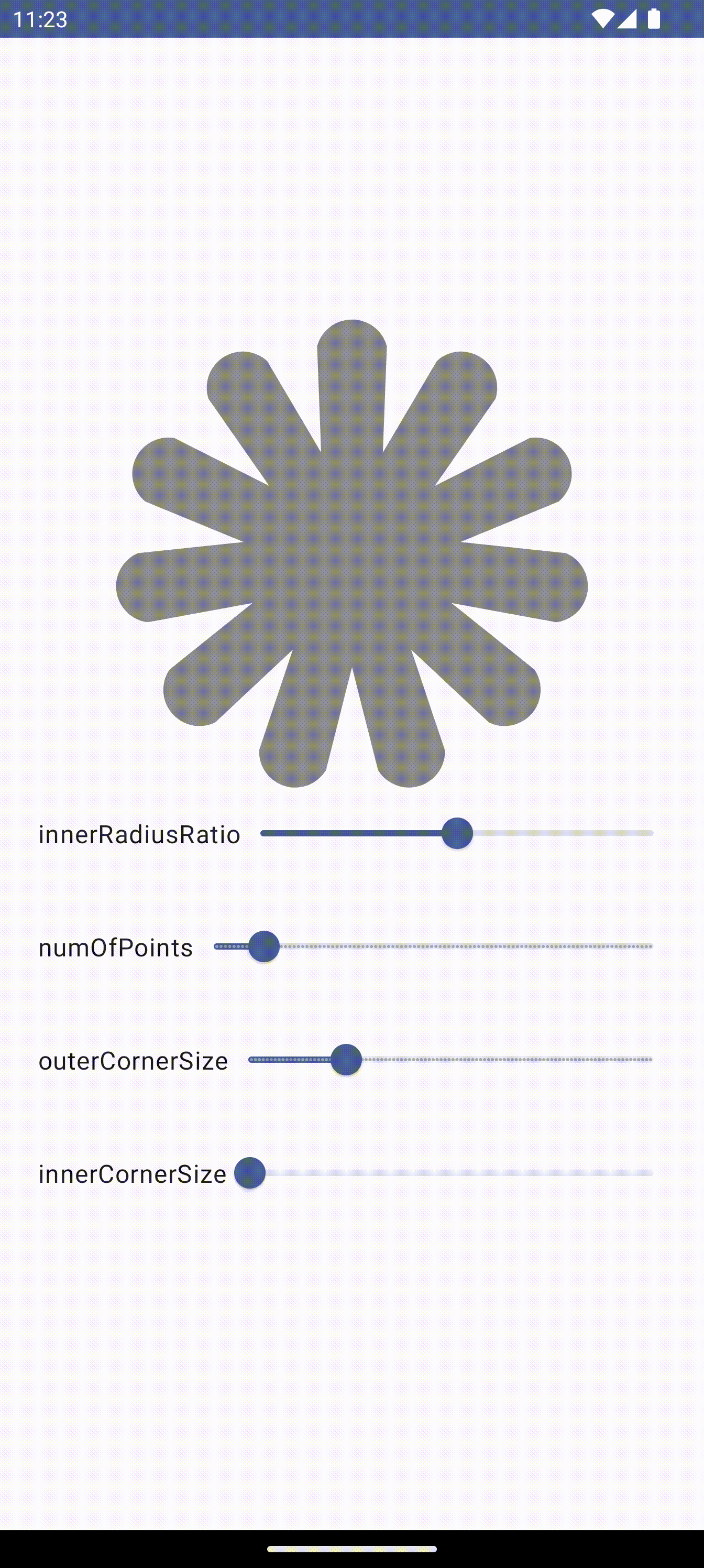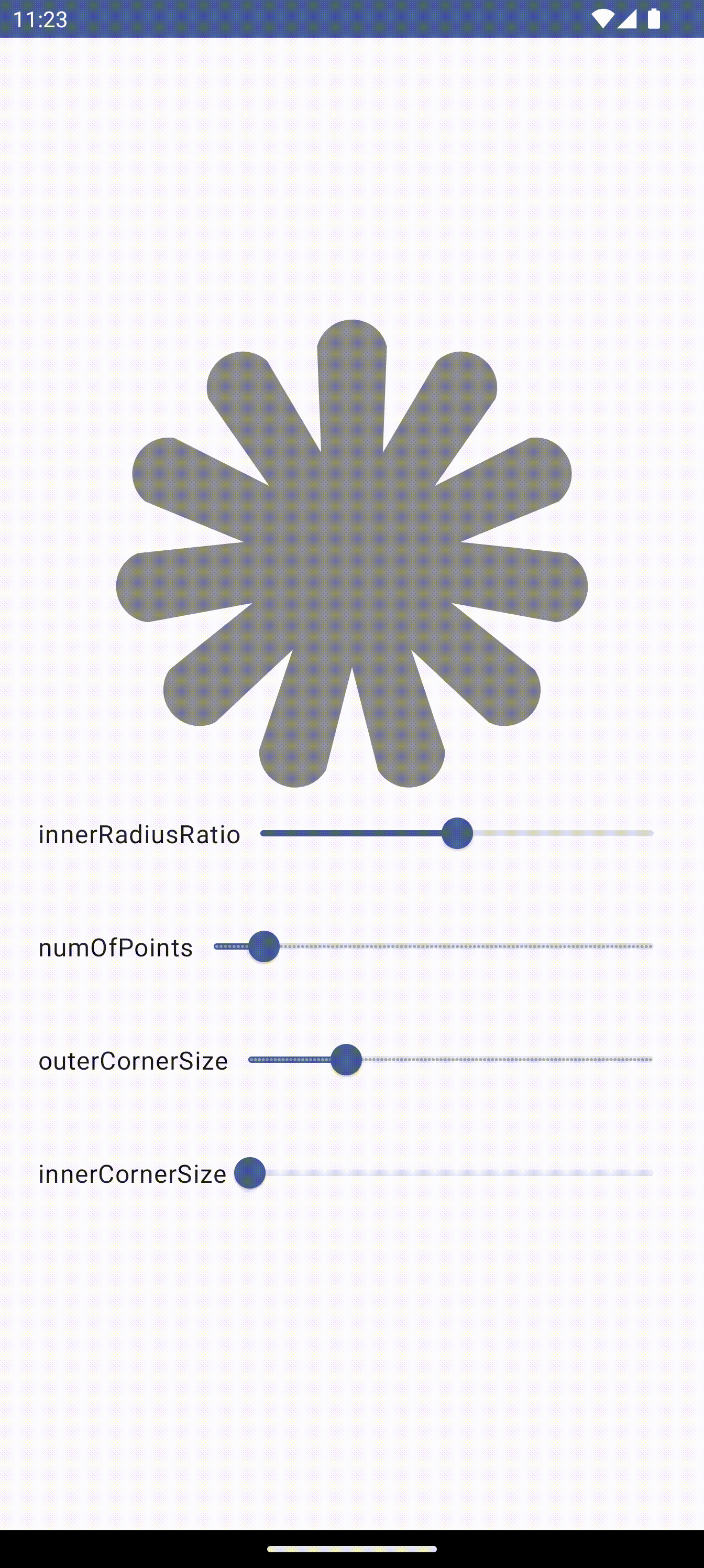꼭짓점의 개수가 클 때는 원 둘레만큼 줄어드는게 아니라 오히려 도형이 커지는? 현상이 발생했다.
원의 반지름 구하기
우리가 처음에 설정해준 cornerRadius값보다 접점과 중심좌표를 구해서 얻은 원의 반지름 값이 작기 때문에 훨씬 바깥쪽에 원이 그려져서 오히려 커지는 현상이 발생한 것이었다.
그럼 처음부터 radius를 설정하고 계산했는데 왜 결과값은 더 적게 측정이 된 걸까?
아무래도 가장 유력한 이유는 오차값 때문인 것 같다. Degree 각도에서 Radian로 바꾸고 비율 구할려고 각도를 또 나누고 곱하고 하는 과정에서 오차가 누적된 것 같다.
그냥 내가 내각을 잘못 계산한 것이었다 ^^ 이 포스팅에 새로 계산한 내용을 작성하였으니 참고하기 바란다.
그래서 결국 다시 anchor좌표와 중심 좌표를 이용해서 원의 지름을 구해주었다.
val arcRadius = sqrt(
(circleCenter.first - anchor1.first) * (circleCenter.first - anchor1.first) +
(circleCenter.second - anchor1.second) * (circleCenter.second - anchor1.second)
)
path.arcTo(
rect = Rect(
offset = Offset(
circleCenter.first.toFloat() - arcRadius.toFloat(),
circleCenter.second.toFloat() - arcRadius.toFloat()
),
size = Size(arcRadius.toFloat() * 2, arcRadius.toFloat() * 2)
),
startAngleDegrees = startAngleDegree.toFloat(),
sweepAngleDegrees = if (i % 2 == 0) sweepAngle.toFloat() else -sweepAngle.toFloat(),
forceMoveTo = false
)원의 안쪽 꼭짓점 둥글게 하기
이렇게 인접한 원을 생각하고 위 방식과 동일하게 진행하면 된다.
결과물
전체 코드
val path = Path()
if (numOfPoints == 0) {
return Outline.Generic(path)
}
val centerX = size.width / 2
val centerY = size.height / 2
val outerRadius = min(centerX, centerY)
val innerRadius = outerRadius * innerRadiusRatio
val innerCircleAngle = 2.0 * PI / (numOfPoints * 2)
val totalPoints = numOfPoints * 2
val innerPointAngleDegree = (totalPoints - 2) * 180f / totalPoints
val outerPointAngleDegree =
innerPointAngleDegree - (360f - innerPointAngleDegree * 2)
var currentCenterAngle = 0.0
val vertices = mutableListOf<Pair<Float, Float>>()
for (i in 0 until numOfPoints * 2) {
val r = if (i % 2 == 0) outerRadius else innerRadius
val x = centerX + (r * sin(currentCenterAngle)).toFloat()
val y = centerY - (r * cos(currentCenterAngle)).toFloat()
vertices.add(Pair(x, y))
currentCenterAngle += innerCircleAngle
}
val dx = vertices[1].first - vertices[0].first
val dy = vertices[1].second - vertices[0].second
val polygonDist = sqrt(dx * dx + dy * dy)
val outerCornerRadius = minOf(
outerCornerSize.toPx(size, density).toDouble(),
polygonDist * tan((outerPointAngleDegree / 2.0).toRadian())
)
val innerCornerRadius = minOf(
innerCornerSize.toPx(size, density).toDouble(),
polygonDist * tan((innerPointAngleDegree / 2.0).toRadian())
)
for (i in vertices.indices) {
val (x, y) = vertices[i]
val (prevX, prevY) = vertices[(i + vertices.size - 1) % vertices.size]
val (nextX, nextY) = vertices[(i + 1) % vertices.size]
val curPointAngleDegree =
if (i % 2 == 0) outerPointAngleDegree else innerPointAngleDegree
val curCornerRadius =
if (i % 2 == 0) outerCornerRadius else innerCornerRadius
val circleTangentDist = curCornerRadius / tan((curPointAngleDegree / 2.0).toRadian())
val tangentRatio = circleTangentDist / polygonDist
val anchor1 = Pair(
prevX + (x - prevX) * (1 - tangentRatio),
prevY + (y - prevY) * (1 - tangentRatio)
)
val anchor2 = Pair(
x + (nextX - x) * tangentRatio,
y + (nextY - y) * tangentRatio
)
var middleX =
((nextX - x) / (nextY - y)) * anchor2.first + anchor2.second -
((x - prevX) / (y - prevY)) * anchor1.first - anchor1.second
middleX /=
((nextX - x) / (nextY - y) - (x - prevX) / (y - prevY))
val middleY =
-((x - prevX) / (y - prevY)) * middleX +
((x - prevX) / (y - prevY)) * anchor1.first + anchor1.second
val circleCenter = Pair(middleX, middleY)
val startAngleDegree = atan2(
anchor1.second - circleCenter.second,
anchor1.first - circleCenter.first
).toDegree()
val endAngleDegree = atan2(
anchor2.second - circleCenter.second,
anchor2.first - circleCenter.first
).toDegree()
var sweepAngle = if (endAngleDegree < startAngleDegree) {
startAngleDegree - endAngleDegree
} else {
endAngleDegree - startAngleDegree
}
if (sweepAngle > 180f) {
sweepAngle = 360f - sweepAngle
}
val arcRadius = sqrt(
(circleCenter.first - anchor1.first) * (circleCenter.first - anchor1.first) +
(circleCenter.second - anchor1.second) * (circleCenter.second - anchor1.second)
)
path.arcTo(
rect = Rect(
offset = Offset(
circleCenter.first.toFloat() - arcRadius.toFloat(),
circleCenter.second.toFloat() - arcRadius.toFloat()
),
size = Size(arcRadius.toFloat() * 2, arcRadius.toFloat() * 2)
),
startAngleDegrees = startAngleDegree.toFloat(),
sweepAngleDegrees = if (i % 2 == 0) sweepAngle.toFloat() else -sweepAngle.toFloat(),
forceMoveTo = false
)
}
path.close()깃헙링크
Frontend Developer