이항분포와 그에 관련된 분포들

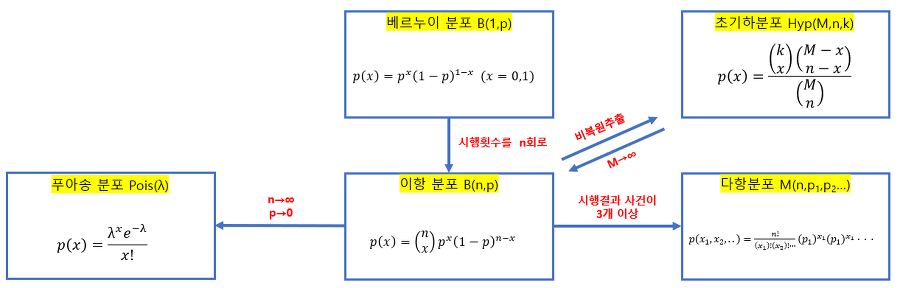
베르누이 시행

---

• 각 시행의 결과가 성공, 실패로 두가지 중 하나만 나오는 경우
• 조건
  1. 각 시행의 결과는 성공(S) 혹은 실패(F) 중 하나로 분류
  2. 각 시행에서 성공확률 p 실패확률 1-p로 그 값은 일정함
  3. 각 시행은 서로 독립

이항분포

---

• $n$ : 시행 횟수

• $p$ : 성공 확률

• $X$ : 성공 횟수 $(1 \leq X \leq n)$

• 확률 질량함수 : $P(X=x)=_{n}\mathrm{C}_{k}p^xq^{n-x}={n \choose x}p^x(1-p)^{n-x}$

• $X$~$Bin(n,p)$

• $E(X) : np$

• $Var(X) : npq$

• $sd(X) : \sqrt{Var(X)}$

기하분포

---

• 베르누이 시행에서 처음 성공이 나올때 까지 시도한 횟수 X의 분포 $X = 1,2,3...$(모든자연수)
• $P(X=x)=(1-p)^{x-1}p$
• $X$~$Geometric(n,p)$
• $E(X) : 1/p$
• $Var(X) : (1-p)/p^2$

음이항분포

---

• 기하분포와 같은 조건이지만 r번째 성공까지의 횟수를 구함 $X = r,r+1,r+2...$(r이상의 모든자연수)
• 기하분포가 음이항분포의 $r=1$일때의 특별한 경우
• $P(X=x)={x-1\choose r-1}(1-p)^{x-r}p^r$
• $X$~$NB(n,p)$
• $E(X) : r/p$
• $Var(X) : r(1-p)/p^2$

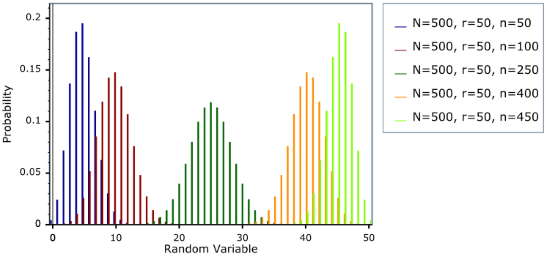
초기하분포

---

• N개의 원소로 이루어진 모집단에서 D개가 집합 A에 속할 때 임의추출한 n개중 A에 속하는 원소의 수
• 원소가 A가 속할때 아닐때 두가지로 나누어 복원추출을 하게되면 앞서 나온 이항분포와 같다. 즉 이항분포와 같은 조건에서 비복원추출을 할때 초기하분포를 따른다
• $P(X=x)=\frac{{D\choose x}{N-D\choose n-x}}{{N\choose n}}$
• $E(X) : np$
• $Var(X) : np(1-p)\frac{N-n}{N-1}$

  유한모집단수정항 : 분산에 있는 $\frac{N-n}{N-1}$을 말하고 모집단이 유한하면서 표본의 크기가 모집단의 크기의 상당부분을 차지말 경우에 비복원추출을 하게되면 확률적으로 큰 영향을 받기에 이 항을 이용하여 수정해 준다. 무한모집단에서 임의추출하거나 유한모집단에서 복원추출하는 경우에는 이항분포를 사용하여도되나 유한모집단에서 비복원추출하는 경우에는 이항분포를 사용하지 못하기에 필요하다. 실제로 모집단의 크기가 표본보다 매우 큰 경우 유한모집단수정항이 근사적으로 1에 가까워지기에 이항분포를 사용해도 상관없으나 모집단의 크기가 작을경우 유한모집단수정항을 가진 초기하분포를 사용하여 문제를 해결한다

포아송분포

---

• 단위시간동안 또는 단위공간에서 평균발생횟수를 뜻함
• 전제조건
  1. 독립성 : 어떤 단위 시간 또는 공간에서 발생한 결과는 다른 시간이나 공간의 결과와 서로 독립이다
  2. 일정성: 단위 시간이나 공간에서 발생한 평균발생횟수는 일정하다
  3. 비집략성 : 매우 짧은 시간이나 작은 공간에서 두 개 이상의 결과가 동시에 발생할 확률은 0이다.
• $X$~$Poisson(m)$
• $P(X=x)=\frac{m^xe^{-m}}{x!}$
• 평균적으로 m회 발생할때 x회 발생할 확률
• $E(X) : m$
• $Var(X) : m$

  포아송분포와 이항분포
  일반적으로 포아송분포는 이항분포에서 오는 것이다. 이항분포의 정의를보면 확률 p인 사건이 n번 시행했을때 k번 발생할 확률이다. 예시로 1일에 사이트을 1명이 올확률이 0.3이라면 20일에 10명이 올 확률은? 이라는 문제를보면
  얼핏보기에는 이항분포로 * $X$~$Bin(20,0.3)$의 모델로 $P(X=10)$를 구하면 될것같다. 하지만 여기서 함정은 하루에 두명이 온다면? 이라는 가정이다. 이러한 부분을 해결하기 위해 포아송분포가 등장했다고 생각하면된다. 포아송분포는 단위시간을 매우 잘게 쪼개어 한 시간에 두개의 사건이 발생하지 못하게 만드는 것을 전제로 한다. 즉 1일에 1명이 올 확률이 0.3이라면 1시간에 1명이 올확률은 24를 나눈 0.0125가된다. 여기서 또 1분으로 나누게되면 약 0.002가 된다. 1초는 물론 0.000003472가 된다. 1일에 1명이 오는데 1초에 두명이 올확률은 거의 0에 가깝다고보면되고 여기서 비집략성 문제를 해결할 수 있게되는 것이다. 이렇게되면 확률은 거의 없더라도 1일에 2명 3명 오는 경우까지 처리할 수 있게된다. 또한 이항분포에서의 n과 p가 m = np로 하여 포아송분포에서는 하나의 변수로 바뀌는데 위 예제에서는 0.000003472*60(초)*60(분)*24(시)*20(일) = 5.999616가 나오고 이렇게 나온 m이라는 변수를 통해 P(X=10)인경우를 구하면 된다. n이 매우크고 p가 매우작은 경우에 경우에 포아송분포를 사용하며 실제로 많이 사용되는 분포이다.

이산확률 분포사이의 관계

---