🥕 목차

• Unit 01 | Vision
  • Vision이란?
  • 시신경의 특징
• Unit 02 | Convolution
  • Convolution 연산
  • 2D-Convolution
  • 채널이 여러 개인 2차원 입력 (3차원)
  • Fully Connected Layer vs. Convolution Layer
• Unit 03 | Convolutional Neaural Network
  • CNN의 구조
  • CNN의 특징
  • Pooling
  • Stride
  • Padding
• Unit 04 | The Number of Parameters

---

Unit 01. Vision

Vision이란?

사람의 눈으로 사물을 보듯이 컴퓨터가 입력을 볼 수 있도록 하는 것

MLP 즉 Fully Connected Network로 이미지를 다루면 이미지는 위 그림처럼 0과 255 사이의 값을 가지는 픽셀로 이루어져 있기 때문에 parameter의 수가 많다.

심지어 컬러 이미지의 경우, 각 픽셀마다 RGB(red, green, blue)에 해당하는 값을 가지기 때문에 parameter의 개수가 너무 많다.

=> 시신경 구조를 모방하는 CNN이 등장!

시신경 특징

1. Topographical Mapping
   대뇌피질에서 서로 가까이 있는 뉴런들은 서로 가까이 있는 물체를 인식하는 특징.
   예) 사람이 사람의 얼굴을 인지할 때, 눈과 코의 위치가 가까이에 있는데 눈을 인식하는 뉴런과 코를 인식하는 뉴런도 서로 가까이 있어 spatial information을 유지

2. Featural Hierarchy
   
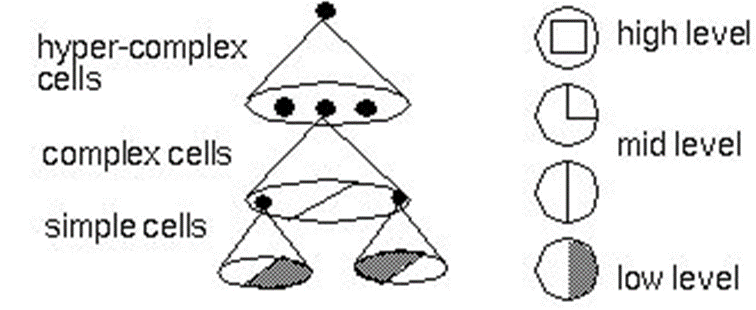
   Feature를 abstract하여 계층적으로 처리하는 특징.
   예) 사람이 사람을 인지할 때, 눈,코,입,손 등을 먼저 인식하고 이를 기반으로 얼굴, 몸통을 인식하고 또 이를 기반으로 사람임을 인지

---

Unit 02. Convolution

Convolution 연산

Convolution(합성곱)은 신호 처리에서 많이 사용되는데, signal을 kernel을 이용해 국소적으로 증폭 또는 감소시켜 정보를 추출 또는 필터링하는 역할을 한다.

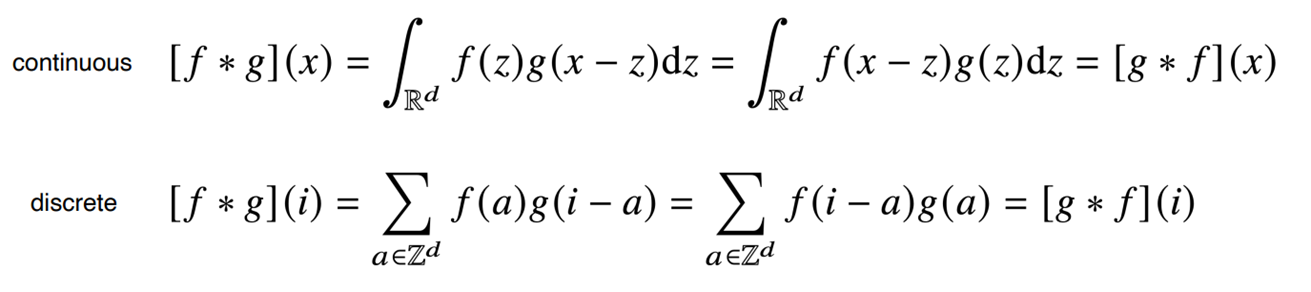
• 위의 두 수식은 정의역이 연속 공간이라 적분을 사용한 것과 이산 공간이라 급수를 사용한 것의 차이일 뿐 적용 방식은 똑같다.
• f(a): 커널 텀, g(i-a): 신호 텀 (입력)
• f(a) 커널 함수가 g(i-a) 입력 함수 위를 이동하면서 element-wise multiplication 즉 원소별로 곱하고 더한다.

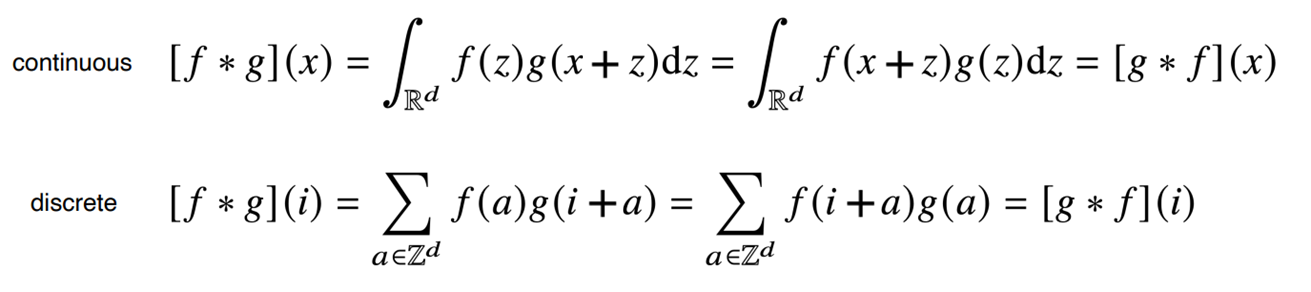
• 사실 CNN에서 사용하는 연산은 위와 같은 cross-correlation(교차 검증)을 사용하지만 관용적으로 convolution이라 한다.

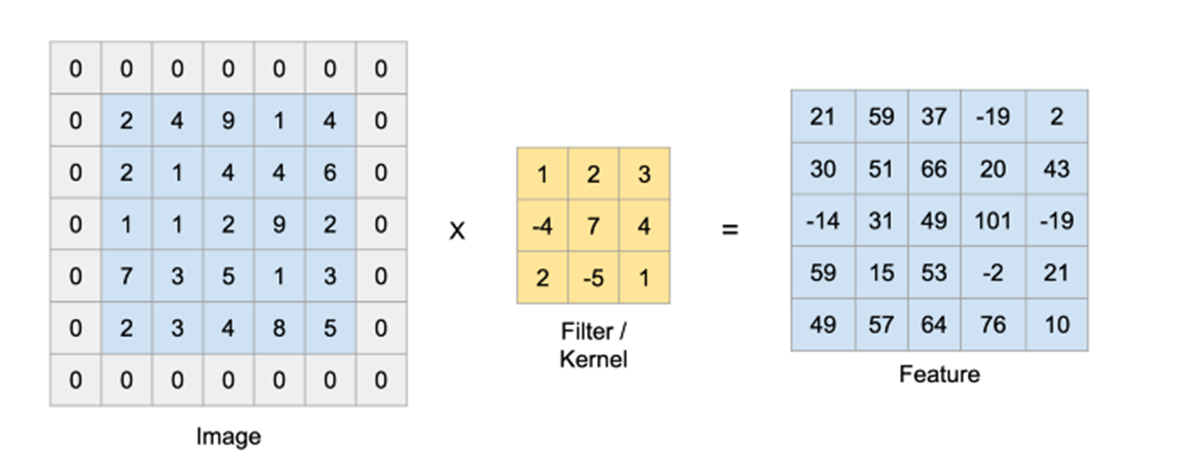
2D-Convolution

2D-Convolution 연산

Convolution은 다양한 차원에서 사용되지만 이미지에 해당하는 2d-convolution을 알아보겠다.

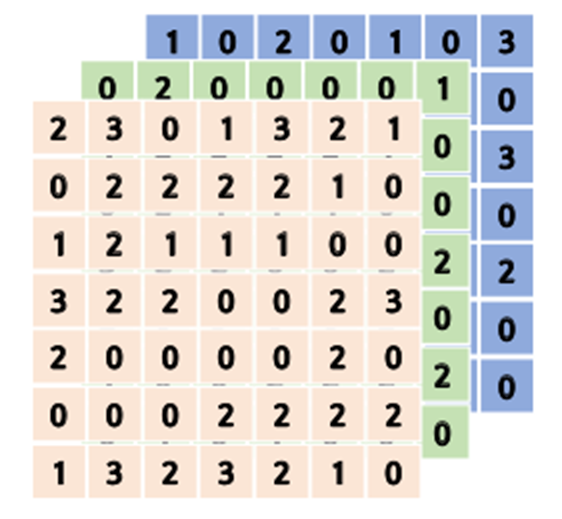
• 초록색 행렬이 커널, 회색 행렬이 input(ex.이미지), 오른쪽 행렬이 output feature map
• 고정된 커널을 그림과 같이 이미지상에서 찍듯 이동해가며 연산한다.
• 커널은 변하지 않고 모든 윈도우에 똑같이 적용되므로 (p,q)는 (1,1), (1,2), (2,1), (2,2)로 값이 고정됨.
• (i,j) 좌표계가 이동하면서 동일한 커널이 적용되는 것. 즉 입력만 바뀌고 커널은 바뀌지 않는다.
• element wise multiplication

output의 크기 계산

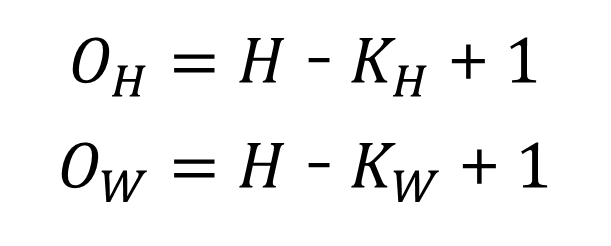
• stride 1, padding 0로 가정 (다른 값을 사용할 경우는 뒤에서 다룸)
• 입력 사이즈: (𝐻, 𝑊), 커널 사이즈: (𝐾h, 𝐾w), 출력 사이즈: (𝑂h,𝑂w)
• 예) 입력 사이즈: (28,28), 커널 사이즈: (5,5) => 출력 사이즈: (24, 24)

채널이 여러 개인 2차원 입력

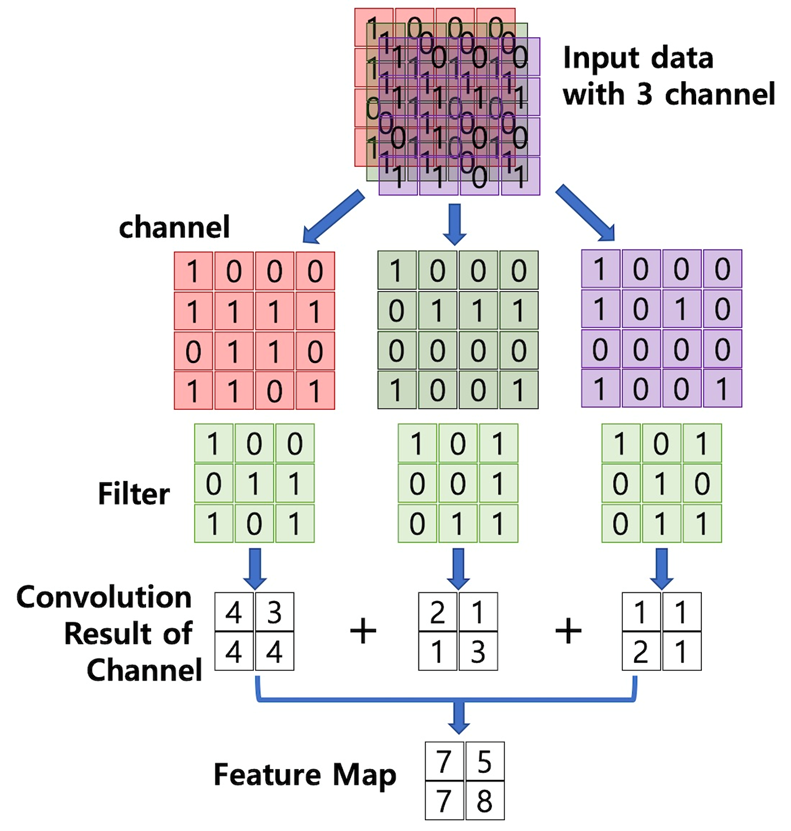
채널 개수만큼 각 convolution filter를 통해 2차원 convolution을 적용하고,
생성된 채널 별 feature map을 element wise sum하여 output의 feature map을 구한다.

=> output의 채널은 1

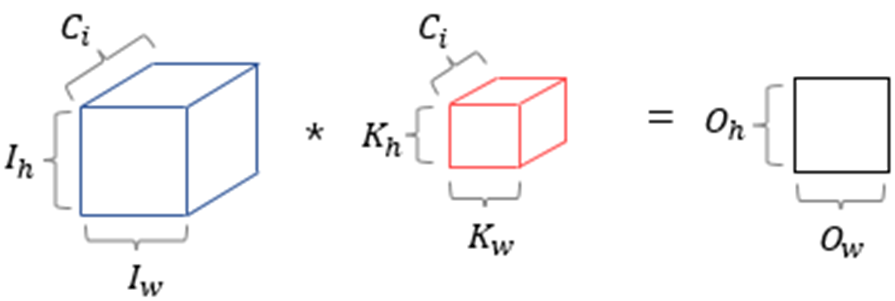
• 채널이 여러 개인 2차원 입력 tensor를 블록으로 표현하면 위와 같음.
• 입력의 채널 = 커널의 채널 = 𝐶𝑖
• 출력의 채널 : 1

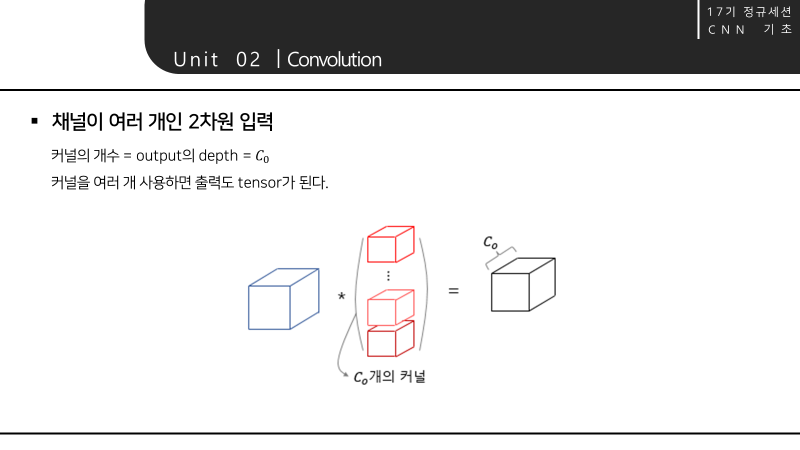
• 출력의 채널을 C0로 출력하고 싶다면 커널을 C0개 사용하면 됨.
• 커널의 개수 = output의 depth = 𝐶0

Fully Connected Layer vs. Convolution Layer

Fully Connected Layer
: 각 뉴런들이 선형모델과 활성함수로 모두 연결된 구조. 각 성분에 대응하는 각 가중치 행이 존재

Convolution Layer
: 고정된 커널을 입력벡터 상에서 이동해가며 선형모델과 활성함수가 적용되는 구조

1. Sparse Connectivity

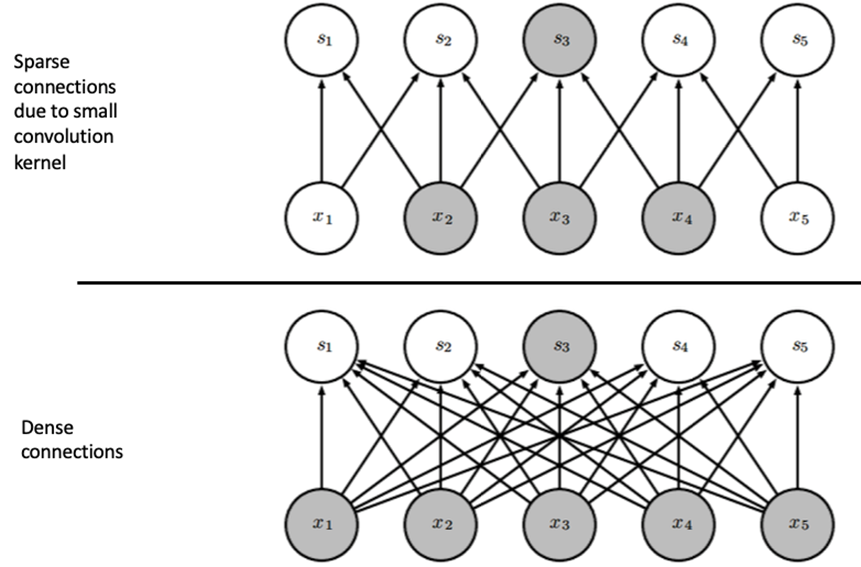
그림
- 위: Conv layer, 아래: FC layer
- 화살표 하나: weight parameter 하나


convolution layer는 sparse connection을 사용하기 때문에 모든 노드가 연결된 fully connected layer와 달리 하나의 output에 특정 subset만 연결된다.
=> weight parameter 개수가 훨씬 적어짐.


하지만 일부 input만 보기에 모든 input을 볼 수 있는 fc layer에 비해 표현력이 줄어드는 것 아니냐, 즉 receptive field가 좁아진다는 문제가 생김.

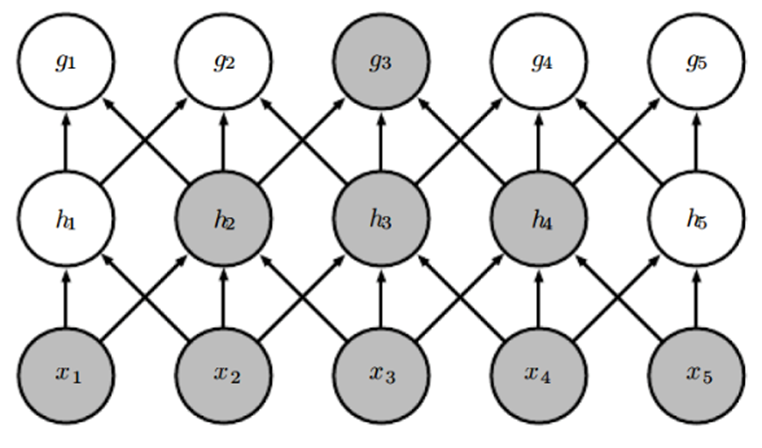
=> Layer를 여러 개 쌓음으로써 문제 해결

2. Parameter Sharing

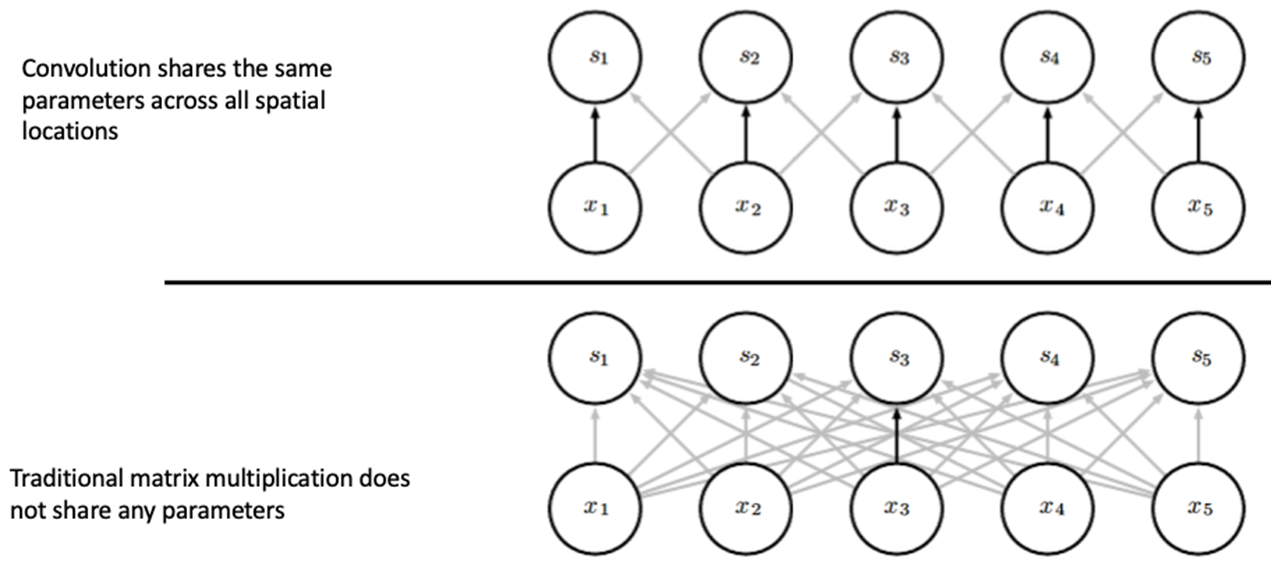
• convolution layer은 fully connected layer와 달리 파라미터를 공유한다.
• 커널을 weight set, weight의 묶음이라고 볼 수 있는데 이 고정된 weight set을 옮겨가며 연산을 반복하기 때문에, 사용되는 weight parameter는 커널을 구성하는 parameter 뿐이다.
• 따라서 같은 방향을 가리키는 화살표는 같은 parameter를 공유.
• 반면 FC Layer는 각 화살표들이 나타내는 parameter가 다 다름.

Efficiency of Convolution

Input size : 320 x 280 / Kernel size: 2 x 1 / output size : 319 x 280

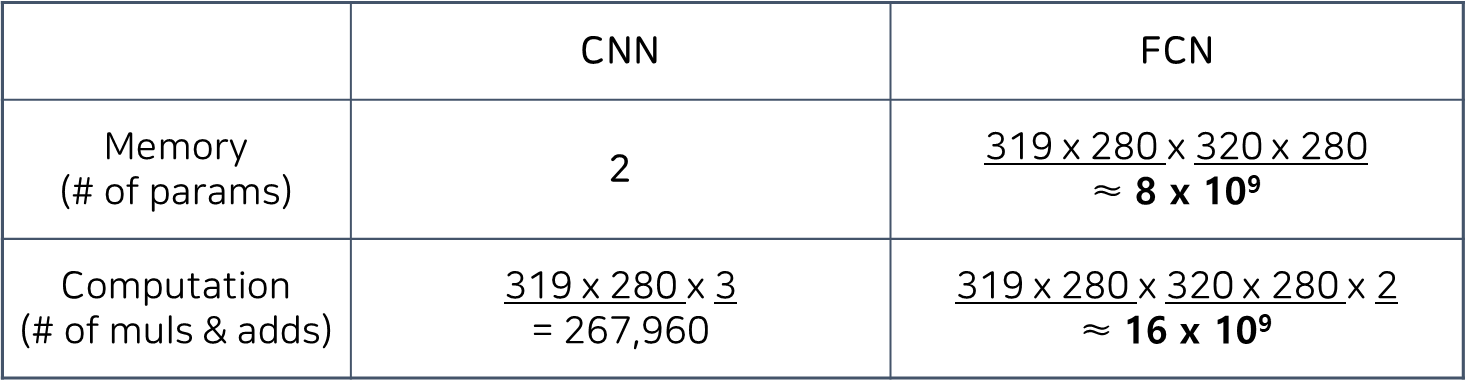
• Memory (# of params)
  CNN : cnn은 같은 커널이라는 weight set을 공유하기 때문에 2x1해서 2개의 parameter만 존재
  FCN : 모든 output 뉴런과 input 뉴런이 개별적인 weight값을 가지므로 output 픽셀의 개수 곱하기 input 픽셀의 개수 = 약 80억개
• Computation
  CNN : output 픽셀 수에 곱하기 2번, 더하기 1번으로 총 3번을 곱함 = 267,960
  FCN : 각 output 픽셀별로 input 픽셀 수만큼 곱셈을 해야 하고 그만큼 더해줘야 하기 때문에 곱셈하나 덧셈하나 해서, 2를 곱함 = 약 160억

=> 여기서 CNN은 FCN에 비해 memory는 약 10억배, computation는 약 10만배 더 좋은 효율성을 가진다.

---

Unit 03. Convolutional Neural Network

CNN의 구조

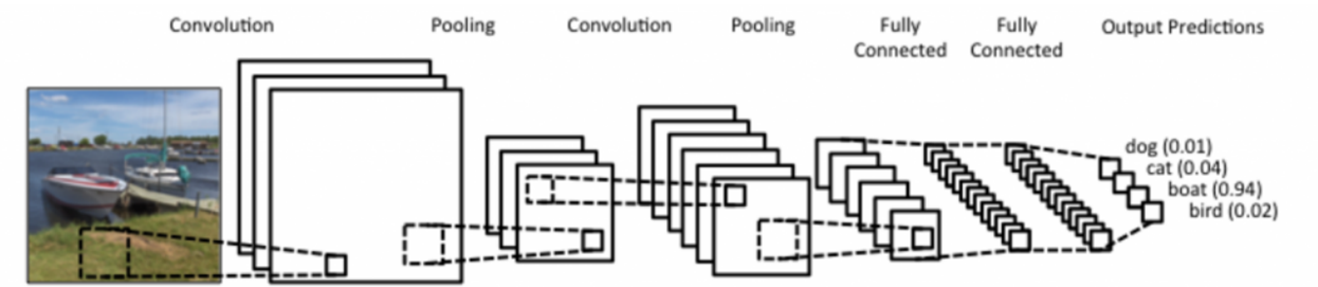
• CNN은 크게 convolution layer, pooling layer, fully connected layer로 구성된다.

• Convolution layer, Pooling layer: 특징 추출
  Fully connected layer: classification

• Convolution Stage
  

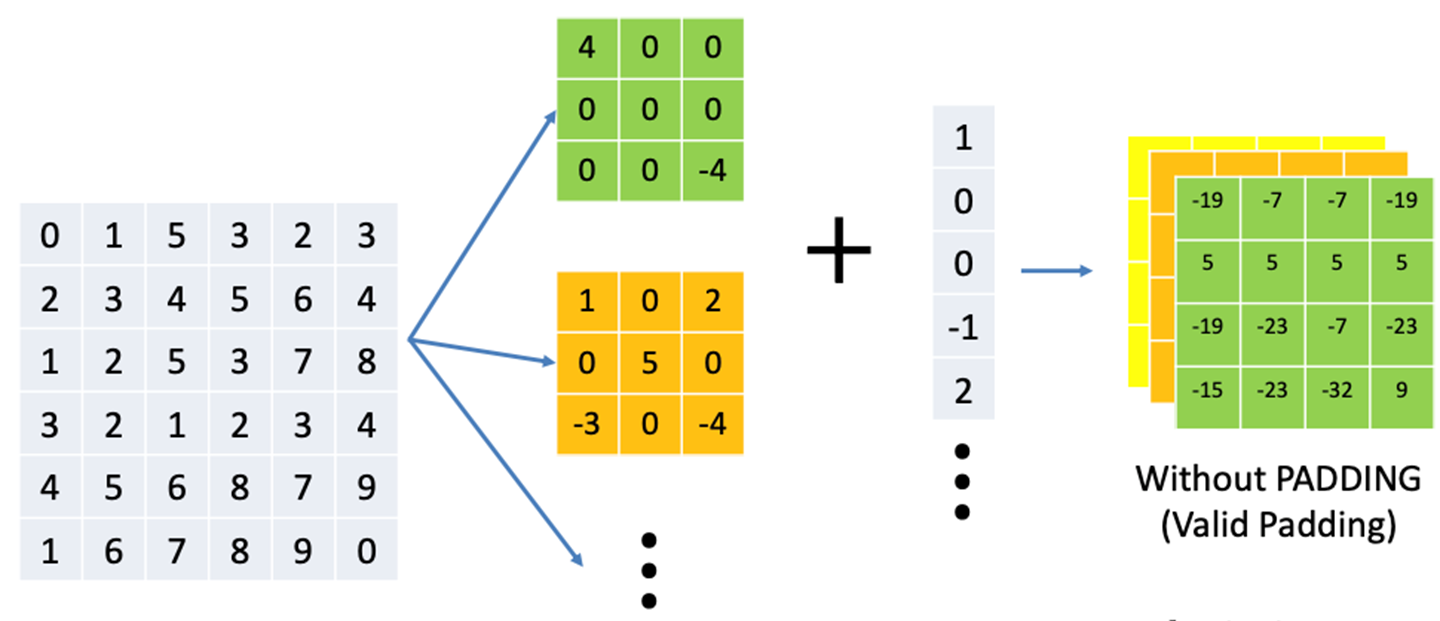
cnn에 입력 이미지가 들어오면 앞에서 다룬 합성곱 연산을 한다.

• Detector Stage
  

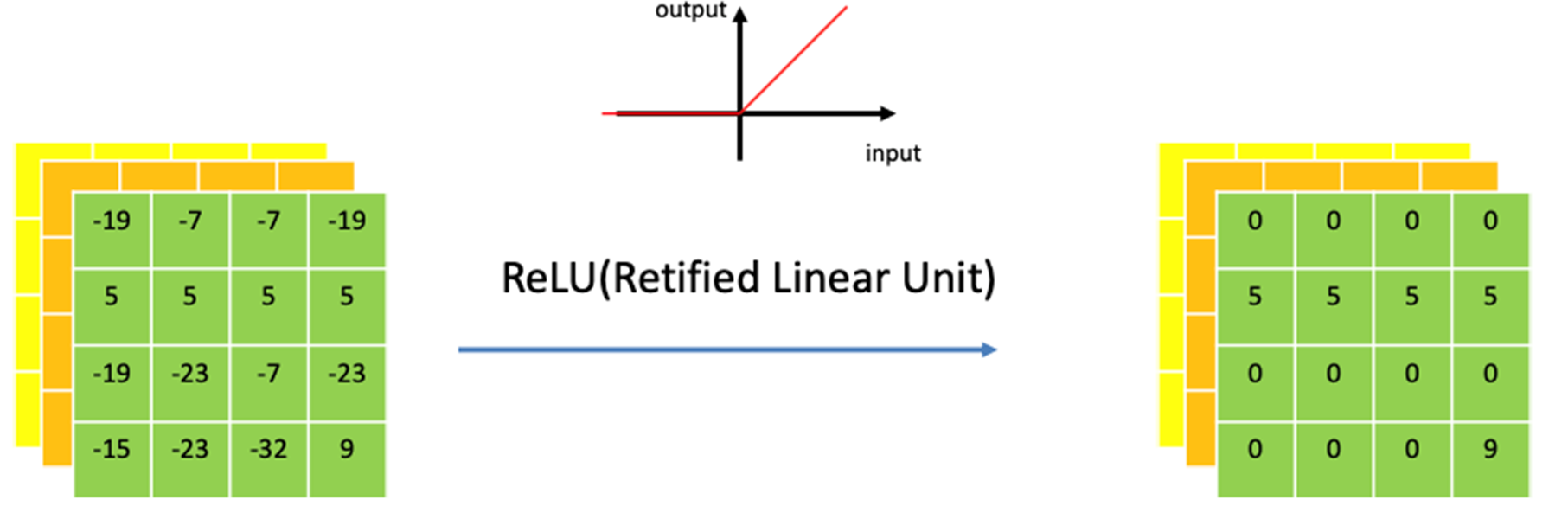
Convolution 연산도 선형연산이므로 비선형성을 주기 위해 convolution 연산이 끝날 때마다 activation function을 적용한다.

• Pooling Stage
  

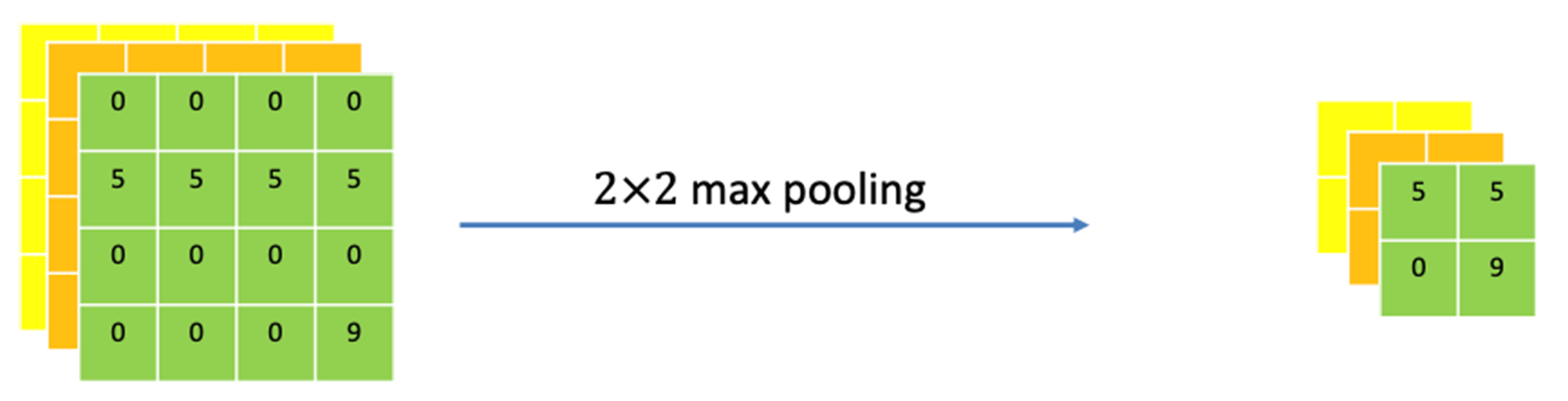
pooling 적용. 뒤에서 자세히 다룰 것이므로 넘어가기.

CNN의 특징

1. Hierarchical Pattern Recognition

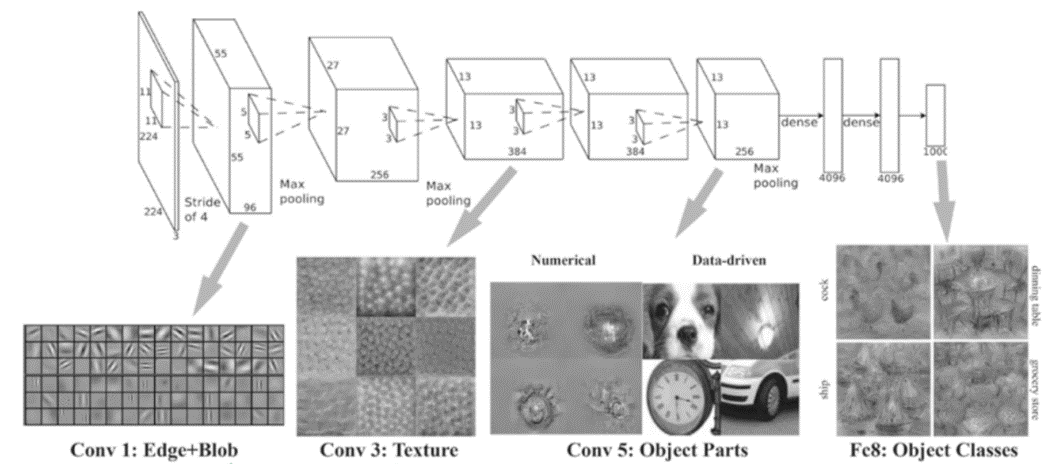
CNN은 시신경을 모방하여 계층적으로 패턴을 인식하는 구조를 가진다고 했는데, 입력층에 가까울수록 엣지, 구석점 등 간단한 저급 특징을 추출하고, 층이 깊어질수록 추상적인 고급 특징을 추출한다.

2. Translation Invariance

cnn은 입력의 작은 이동에 둔감하다는 특징이 있는데, 이는 뒤에 max pooling과 함께 재등장 예정

Pooling

Max Pooling vs. Average Pooling

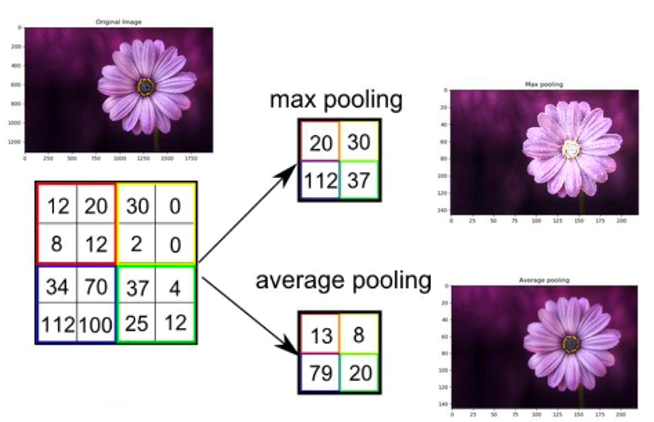
Max Pooling: 윈도우에 해당하는 가장 큰 값을 추출 => 밝은 이미지
Average Pooling: 윈도우의 평균값을 추출 => smoothing된 이미지

가장 중요한 특징을 추출해야 한다는 관점에서 일반적으로 max pooling을 사용한다.

pooling의 효과 1 - Down sampling

• 사이즈를 줄여 불필요한 연산을 줄이고 parameter 수를 줄여 overfitting을 방지한다.
• 선형결합이 아니기 때문에 weight가 없어 학습이 일어나지 않는다.
• 채널 수는 변함 없다.

pooling의 효과 2 - Translation Invariance

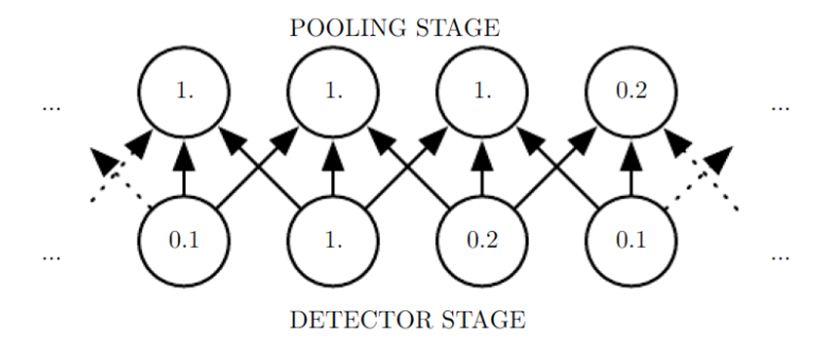
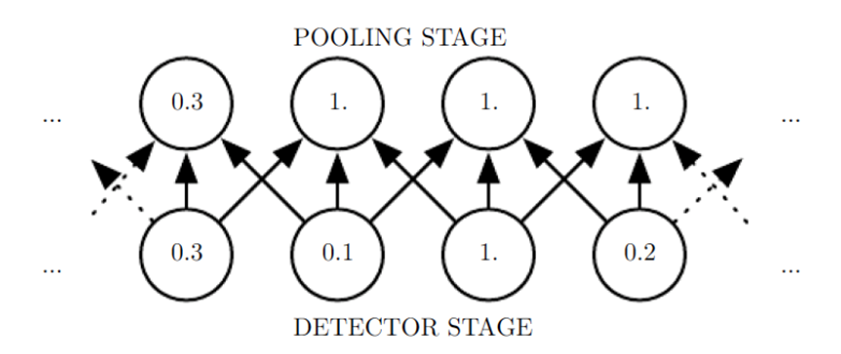
• 작은 이동에 둔감하다 = 이미지 내에서의 위치에 관계없이 동일한 패턴을 동일하게 인식한다.
  예) 고양이 사진에서 고양이 귀가 가운데에 있으나, 오른쪽 구석에 있으나 동일하게 귀라는 패턴을 인식
• 그림과 같이 3x1 max pooling을 사용하는 경우, 해당하는 3개의 input 픽셀 중 가장 큰 값을 output으로 찾아주는 operation을 수행한다.
• 두 번째 그림은 첫 번째 그림의 input을 오른쪽으로 한칸씩 밀어본 결과인데, input을 이동시켜도 output값들이 크게 변하지 않는다. = spatial invariance

Stride

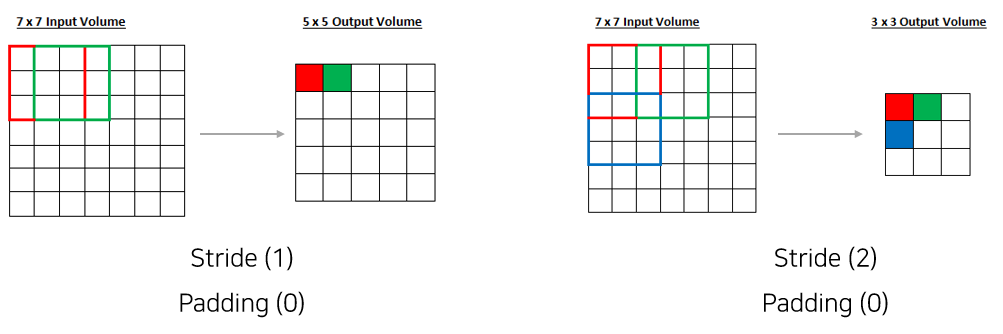
• Filter 적용 시 이동 간격을 의미한다.
• Stride를 키우면 차원을 더 급격히 줄일 수 있다.
• Output의 차원이 정수(integer)가 되도록 Stride를 설정한다.

Stride를 포함한 output size 계산

Output size = (N - F) / S + 1

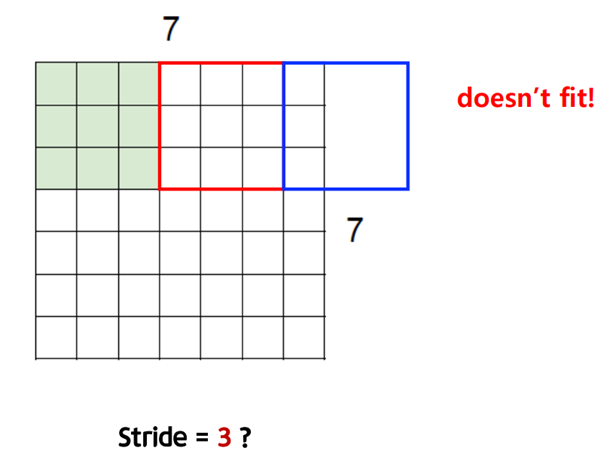
Stride = 1 -> Output size = 5
Stride = 2 -> Output size = 3
Stride = 3 -> Output size = 2.33

=> 이런 식으로 크기가 맞지 않으면 맞지 않는 라인의 정보는 버려지게 되기 때문에 stride를 설정할 때 output size가 정수가 되도록 설정한다.

Padding

• 데이터 가장자리에 fake pixel을 붙여 연산하는 것.
• padding 시키는 값은 인접한 값으로 덧대거나 다른 값으로 채울 수 있지만 일반적으로 0으로 덧대는 zero padding을 사용

Padding의 효과

• 크기 손실 방지
  : convolution 연산을 거치고 나면 output size가 줄어든다. 이 같은 크기 손실을 방지하기 위해 input 데이터 가장자리에 fake pixel을 붙인 후 연산을 하여 합성곱 계층의 출력이 입력 데이터의 공간적 크기와 동일하게 맞춰주는데, 이렇게 fake pixel을 덧대는 것을 padding이라고 한다.
  
  
• 테두리 정보 활용
  : 패딩을 사용하지 않을 경우, 데이터의 Spatial 크기는 Conv Layer를 지날 때 마다 작아지게 되므로, 가장자리의 정보들이 사라지는 문제가 발생한다.
  또한 패딩을 하지 않고 커널 도장을 그냥 찍으면 테두리에 있는 픽셀들은 가장자리에 있으니까 다른 픽셀들에 비해 도장을 찍히는 횟수가 적어서 중앙부와 모서리 픽셀이 합성곱에 기여하는 비율에 큰 차이가 발생한다. 따라서 만약 모서리에 중요한 정보가 있다면 해당 정보는 특성 맵에 잘 전달되지 못함.
  => 적절한 padding은 테두리 정보를 활용할 수 있게 한다.

Padding의 크기 결정
아웃풋 사이즈를 인풋 사이즈와 같게 할 경우, Padding size = (𝐹−1)∕2

커널의 사이즈가 짝수인 경우에 나누어 떨어지지 않아서 대칭적으로 패딩할 수 없는 문제, 중앙부가 생기지 않는 문제가 있음.
=> 여러 가지 관습적, 실험적으로 보통 1,3,5 같은 홀수 크기의 커널을 사용한다.

Stride, Padding을 포함한 output size 계산

Output size = (𝑁−𝐹+2𝑃)∕𝑆−1

위의 padding size 계산식을 p에 대입하면 Output size가 N이 나와서 Input size와 같은 것을 확인할 수 있다.
만약 나누어 떨어지지 않으면 내림을 사용하면 된다.

---

Unit 04. The number of parameters on CNN

Padding (1), Stride (1), 5 x 5 Kernel

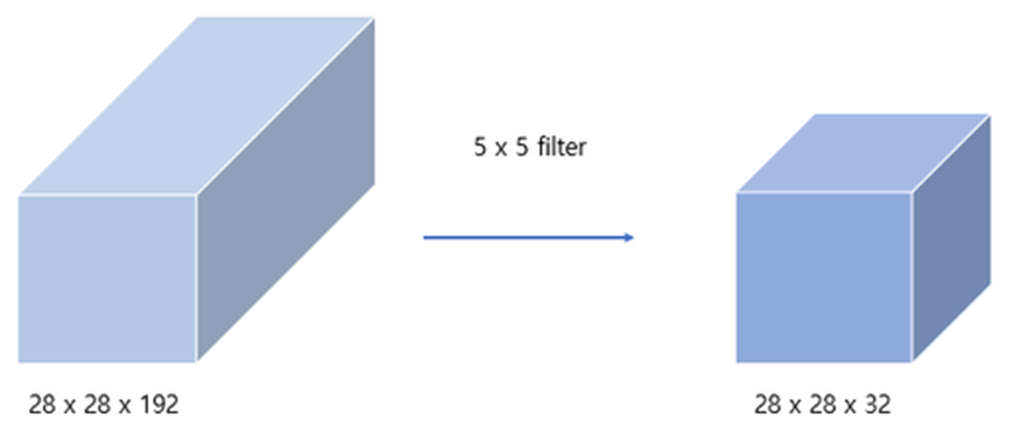
padding의 크기가 1, stride가 1 이고 인풋 사이즈와 커널 사이즈 그리고 아웃풋 사이즈가 다음과 같이 주어졌을 때, parameter의 개수는 다음과 같다.

커널의 채널은 input 채널과 같으므로
필터 하나당 파라미터 개수 = 5x5x192+1
커널의 개수가 output의 depth를 결정하므로
필터의 개수 = 32

정리하자면,
kernel 채널 = input 채널, kernel 개수 = output 채널이므로

parameter 개수 = (kernel size + bias) x input channel x output channel

---

References

14기 이정은님 강의
15기 황보진경님 강의
이정우 교수님 딥러닝의 기초 강의 - 201029 Chapter7
Stanford cs231n 강의
김성훈 교수님 PyTorch Lecture 10: Basic CNN
http://taewan.kim/post/cnn/
https://yjjo.tistory.com/8