하루5분코딩"Graph"

## Graph : 노드 그리고 노드와 노드를 연결하는 edge의 구성

✓tip 그래프는 무방향(undirected)과 방향(directed) 일수있다. "무방향"은 연결된 노드가 대칭, 즉 서로를 가리킨다고 볼수 있고 "방향"은 노드의 비대칭, 즉 한쪽에서만 가리킨다고 볼수있다.

How to search "graph"

- DFS(Depth-First search) 깊이 우선 검색

- BFS(Breadth-First search) 넓이 우선 검색

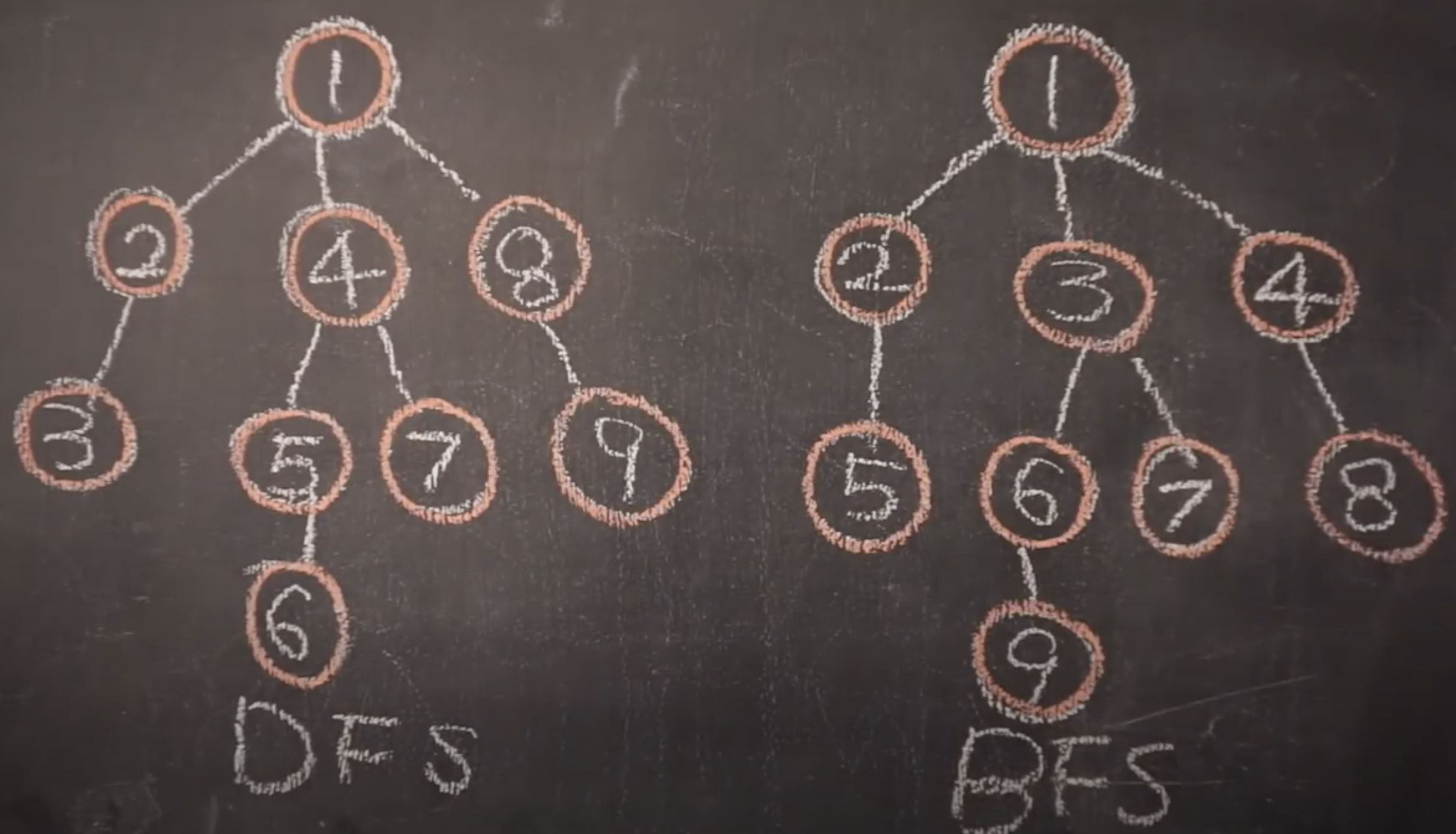
How to use searching skill

- Stack 이나 Queue 에 들어갔다가 빼주면서 출력 그리고 연결된 노드를 넣어준다

- DFS 는 주로 Stack 으로 사용하고, BFS 는 Queue 에서 사용한다.

✓Reference - https://www.youtube.com/watch?v=_hxFgg7TLZQ

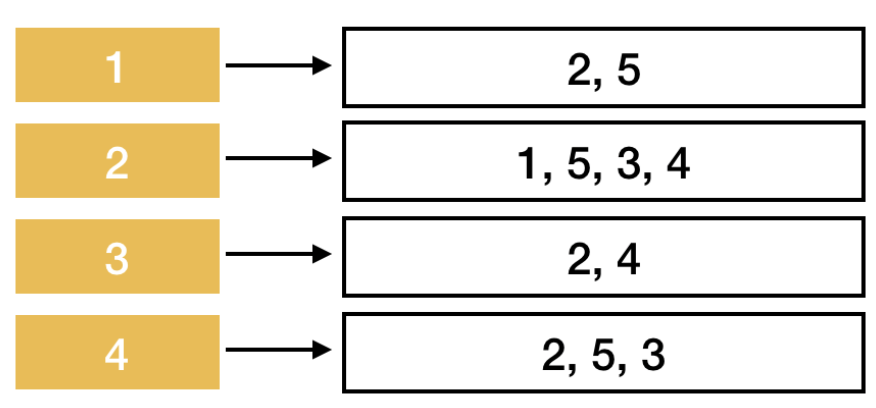
인접 행렬과 인접 리스트

- 인접 리스트: 정점을 노드의 키로 사용하며 해당 노드의 이웃들을 리스트에 저장한다.

- 인접 행렬 : 행렬의 각 항목이 두 정점 간에 연결을 나타내는 V*V 행렬이다.

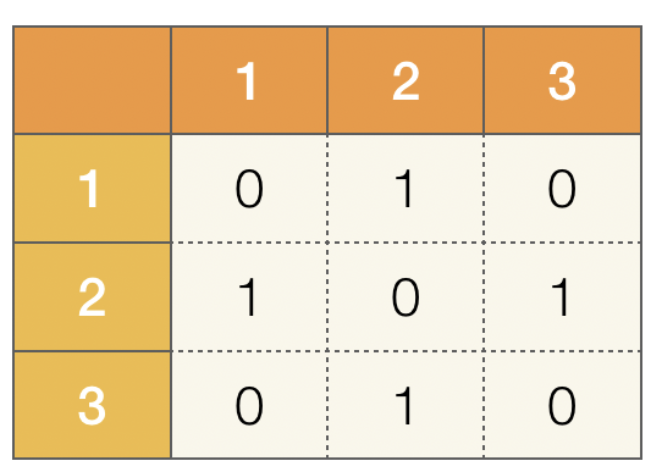
진입 차수와 진출 차수

-한 정점에 도착하는 edge수

-한 정점에서 출발하는 edge 수

둘을 더하면 차수 가 된다.

✓ Method

• addNode(node) - 그래프에 노드를 추가합니다.
• addEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 추가합니다.
• removeNode(node) - 그래프에서 노드를 삭제합니다.
• removeEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선을 삭제합니다.
• hasEdge(fromNode, toNode) - fromNode와 toNode 사이의 간선 존재 여부를 반환합니다.
• contains(node) - 그래프에 해당 노드가 존재하는지 여부를 반환합니다.

✓ 사용

addNode(node) {
    this.nodes[node] = this.nodes[node] || [];
  }

contains(node) {
    return this.nodes.hasOwnProperty(node);
}

removeNode(node) {
  for (let key of this.nodes[node]) {
    this.removeEdge(node, key)
  }
  delete this.nodes[node]
}

hasEdge(fromNode, toNode) {
  for (let key of this.nodes[fromNode]) {
    if (key === toNode) {
      return true;
    }
  }
  return false;
}

addEdge(fromNode, toNode) {
  this.nodes[fromNode].push(toNode)
  this.nodes[toNode].push(fromNode)
}

removeEdge(fromNode, toNode) {
  let from = this.nodes[fromNode]
  let to = this.nodes[toNode]
  from.splice(from.indexOf(toNode), 1)
  to.splice(to.indexOf(fromNode), 1)
}