문제 출처
https://school.programmers.co.kr/learn/courses/30/lessons/42839#(프로그래머스)
학습 키워드
완전탐색
시도 방법
(1) 조합 가능한 경우의 수를 재귀로 풀이
(2) count 를 static 처리하여 소수일 경우 숫자 카운트
(3) set 개념을 활용해 이미 소수판별된 중복값은 추가로 카운트 하지 않음
내가 작성한 코드
이번 문제는 풀면서 시간도 오래걸렸다.
기존의 조합을 할 수 있는 라이브러리를 사용하지 않고 자체적으로
문제를 풀어보고 싶었다.
비록 성능이나 속도 등은 비효율일지라도 끈질기게 파고들어 해결한 문제였다.
import java.util.HashSet;
class Solution {
static int count = 0 ;
static HashSet<Integer> set = new HashSet<>();
public int solution(String numbers) {
String[] splitNumbers = numbers.split("");
recursive(splitNumbers , "" , 0 , splitNumbers.length);
return count;
}
public void recursive(String[] numbers , String now , int start , int end) {
if(start > end) {
return;
}
checkSosu(now);
for(int i = 0 ; i<numbers.length; i++) {
if(numbers[i] != null) {
String data = now + numbers[i];
String[] tmp = numbers.clone();
tmp[i] = null;
recursive(tmp, data , start+1, end) ;
}
}
}
public void checkSosu(String num) {
if(num.equals("")) return;
int numToInt = Integer.parseInt(num);
if(numToInt <= 1 || set.contains(numToInt)) return ;
if(numToInt == 2) {
set.add(numToInt);
count++;
return;
}
for(int i = 2; i<numToInt; i++) {
if(numToInt%i == 0) {
return;
}
}
count++;
set.add(numToInt);
}
}코드설명
[main 메서드]
static int count = 0 ;
static HashSet<Integer> set = new HashSet<>();
public int solution(String numbers) {
String[] splitNumbers = numbers.split("");
recursive(splitNumbers , "" , 0 , splitNumbers.length);
return count;
}
소수의 개수를 카운트하기 위한 count를 전역 변수로 설정했다.
그리고 이미 카운트한 소수가 중복될 수 있기에 HashSet을 이용해 중복 카운트를 하지 않도록 초기화했다.
만약 "17" 이라면 다음과 같은 경우의 수가 가능하다. ( "1" , "7" , "17" , "71" )
중요한 점은 이 문제는 비복원 추출이다
그래서 11 이나 77 등의 값은 불가능하다는 것을 경우의 수에 녹여야 했다.
[recursive 메서드 - 모든 조합의 경우를 구하는 기능]
public void recursive(String[] numbers , String now , int start , int end) {
if(start > end) {
return;
}
checkSosu(now);
for(int i = 0 ; i<numbers.length; i++) {
if(numbers[i] != null) {
String data = now + numbers[i];
String[] tmp = numbers.clone();
tmp[i] = null;
recursive(tmp, data , start+1, end) ;
}
}
}numbers 는 위 main에서 split한 문자열 배열이다.
"17" 이라면 ["1" , "7"] 로 구성이 되는 값이다.
now는 현재 조합의 값이다.
예를 들어 "1" 이라는 값으로 재귀함수를 호출하면
그 다음에는 "17" 과 같이 now + 새로추가할배열값으로 다시 메서드를 호출한다.
여기서 String[] tmp = numbers.clone() 이 핵심 아이디어였다.
만약 ["1", "2" , "2" ,"4"] 가 numbers 로 주어졌다고 가정해보자.
"1" 이 now 이고 그럼 이후에 가능한 조합은 "12" , "12" , "14" 가 된다. (즉 "11" 은 불가능하다)
따라서 새로운 numbers를 클론(복사)하고 해당 인덱스의 값을 null 처리해서
다음 재귀에서는 [null , "2" , "2" , "4" ] 를 numbers 로써 사용하는 것이다.
위 조건을 보면 null이 아닌 경우에만 로직이 흐르기 때문에 결과적으로
"12" , "12" , "14" 라는 조합에 대해 처리가 되고
만약 "12"라면 인덱스가 1인 상태이니까 이를 또 null 처리하고 보내면
[null , null , "2" , "4"] 라는 numbers 와 "12" 라는 now값으로 또 진행을 하게된다.
[checkSosu메서드 - 소수인지 판별하는 기능]
public void checkSosu(String num) {
if(num.equals("")) return;
int numToInt = Integer.parseInt(num);
if(numToInt <= 1 || set.contains(numToInt)) return ;
if(numToInt == 2) {
set.add(numToInt);
count++;
return;
}
for(int i = 2; i<numToInt; i++) {
if(numToInt%i == 0) {
return;
}
}
count++;
set.add(numToInt);
}소수를 판별하는 메서드이다.
소수하면 전역변수인 count을 1 추가하고, set에 소수를 추가함으로써
이후에 추가로 count하지 않도록 한다.
실행결과
새롭게 알게된 점
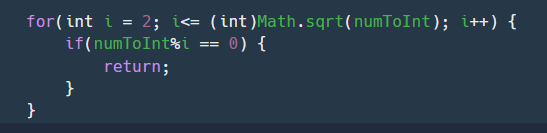
(1) 소수 판별할 때 굳이 전체를 비교하는게 아니라 그 제곱근까지만 비교하면 성능을 좀 더 올릴 수 있겠다는 생각을 했다. (Math.sqrt() 등을 이용)
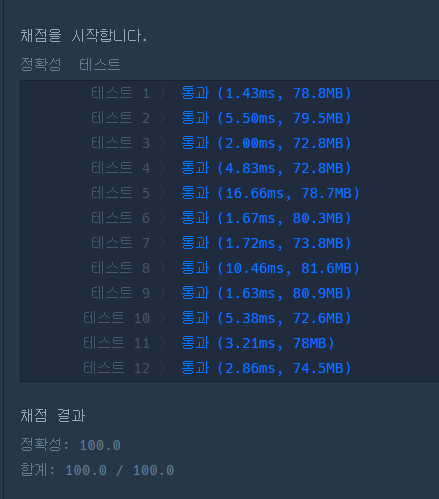
실제로 속도면에서 눈에 띄는 개선이 확인되었다. (공간은 비슷했다)
다음에 풀어볼 문제 - 타겟 넘버
#99클럽 #코딩테스트 준비 #개발자 취업 #항해99 #TIL
