문제 List
- 1463번: 1로 만들기
- 11726번: 2*n 타일링
- 11727번: 2*n 타일링
- 9095번: 1, 2, 3 더하기
- 10844번: 쉬운 계단 수
- 11057번: 오르막 수
- 2193번: 이친수
문제
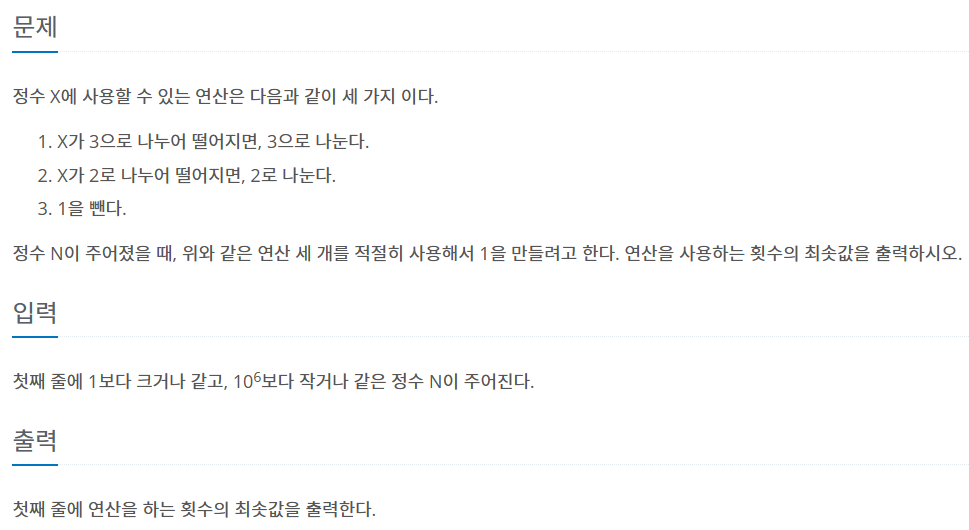
1463 1로 만들기
코드
#include <bits/stdc++.h>
using namespace std;
int input(){
int n;
cin >> n;
return n;
}
void sol(int n){
vector<int> dp(n+1);
dp[1] = 0, dp[2] = 1, dp[3] = 1;
for(int i = 4; i <= n; i++){
dp[i] = dp[i-1] + 1;
if(i % 2 == 0) dp[i] = min(dp[i/2] + 1, dp[i]);
if(i % 3 == 0) dp[i] = min(dp[i/3] + 1, dp[i]);
}
cout << dp[n] << '\n';
}
int main(){
sol(input());
}풀이
주어진 값을 체크하고 나눠보고 몇 개일지 하나씩 구해보는 느낌으로 생각하면 풀 수가 없었다.
도감에서 주어진 숫자에 대한 값을 가져온다는 생각을 하며 문제를 풀어 나가는 것이 좋았다.
그렇다면 도감을 채워보자
- 입력 값을 채우기 위한 도감의 준비물을 채우자
- 고정된 값을 도감에 넣는다
ex ) dp[1] = 0, dp[2] = 1, dp[3] = 1 - 고정된 값을 기준으로 앞으로 들어올 값들은 어떤 규칙을 가지고 값을 가지는지 분석한다.
- 해당 기준을 반복시켜도 해당하는지 확인하고 입력 값을 출력하도록 한다.
문제
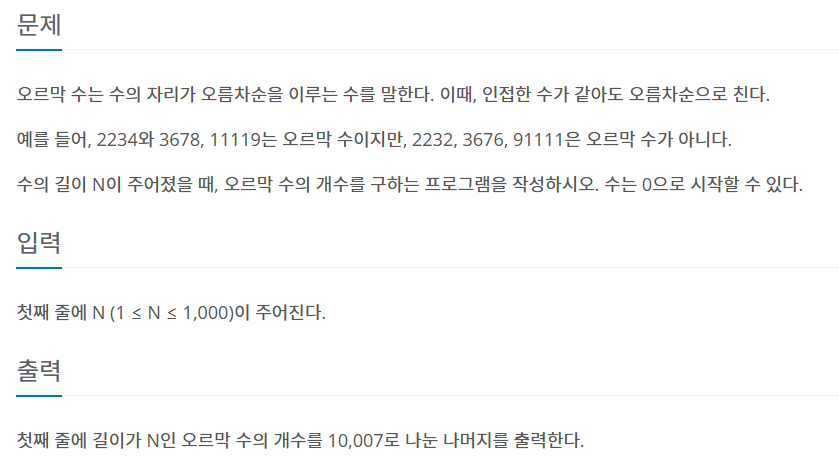
11057 오르막 수
코드
#include <bits/stdc++.h>
using namespace std;
int n;
void input(){
cin >> n;
}
void sol(int num){
int dp[1004][10] = {0, };
int ret = 0;
for(int i = 0; i < 10; i++){
dp[1][i] = 1;
}
for(int i = 2; i <= num; i++){
for(int j = 0; j < 10; j++){
for(int k = 0; k <= j; k++){
dp[i][j] += (dp[i-1][k] % 10007);
}
}
}
for(int i = 0; i < 10; i++){
ret += (dp[num][i] % 10007);
}
cout << ret % 10007 << '\n';
}
int main(){
input();
sol(n);
}풀이
위와 같은 풀이로 접근했다.
규칙을 찾는데 1차원으로 규칙을 표현하기에 부족하다는 생각이 들었다.
dp[자릿 수][마지막에 오는 수] 로 규칙을 표현하고 싶다는 생각이 들어 2차원 DP 배열로 문제의 규칙을 찾기 시작했다.
입력 값은 "자릿 수" 였다. 이를 간과한채로 2차원 배열을 dp[1004][1004]로 미리 선언해두었다.
계속 오류가 나는 부분이었다.
프로그램에서 간혹 큰 배열을 실행하는데 오류가 생겨서 배열은 입력 값에 맞는 크기로 지정하는 것이 좋다고 한다.
"마지막에 오는 수"는 0 ~ 9까지 10개밖에 되지 않기에 1004개의 배열을 지정해줄 필요가 없던 것이다.
위 문제의 규칙은 자릿 수 마다 끝자리에 오는 수를 생각하여
ex ) 1자리 숫자의 끝이 0과 1인 수 0 , 1은 2자리 숫자가 될 때 00, 01, 11, 12가 될 수 있다.
즉, 2자리 숫자 중 끝자리가 1인 수는 이전자리 숫자(1자리 숫자) 중 끝자리가 자기보다 작은 (0, 1)을 합하면 되는 것이다.
이러한 규칙을 기반으로 코드를 설계했다.
후기
DP 관련 문제는 이전에 가장 어려웠고 감이 안잡히는 분야였다.
풀이를 봤을 때는 이해가 됐지만 스스로 문제를 풀어나가는 과정이 정말 어려운 분야였다.
스스로 풀어봤던 문제 + 비슷한 유형의 안 풀어본 문제를 풀어보며 감을 다시 잡았다.
"도감"을 채운다는 느낌을 얻은 것은 정말 큰 도움이 됐다.
조금 더 배우고 DP에 대해 알수록 표현 하는 방법이 풍부해지겠지만 현재로썬 정말 좋은 표현이라 생각한다.
아 이번에 객체지향설계패턴이라는 수업을 들으며 코드를 객체지향적으로 설계하는 것이 얼마나 좋은지 깨닫고 있어서 코드를 최대한 함수화 시키며 함수를 끌어다 쓰는 방식으로 짜보고 있다.
알고리즘 문제 중 클래스까지 설계해서 유지보수를 해야하는 정도의 수준을 요구하는 문제는 아직 못봤지만 코드를 함수화 시켜서 오답일 때도 쉽게 고칠 수 있게 해보려고 코드 스타일을 바꿔보았다.
DP는 기본 문제 시리즈 3정도까지 진행하려고 한다.
