들어가기에 앞서
학교 수업시간에 코틀린으로 프로젝트를 할 일이 있어 코틀린 관련 서적을 찾으러 도서관을 둘러보다가 너무 흥미로운 제목을 가진 책이 있어서 빌렸다.
재미있어 보이니 알고리즘, 자료구조 공부도 할 겸 틈틈이 읽으면서 간단하게 기록이나 남겨야겠다.
복잡도와 빅오 표기법
복잡도란?
어떤 문제를 푸는 알고리즘은 보통 여러개다. 더 나은 알고리즘을 판단하기 위해 기준이 필요한데 복잡도가 중요한 역할을 한다.
빅 O 표기법
알고리즘 A의 계산 시간 T(N)이 대략 P(N)에 비례하면 T(N) = O(P(N))이라 표현하고, 알고리즘의 복잡도는 O(P(N))이라 부른다.
어떤 알고리즘 계산 시간 T(N)이
T(N) = 3N^2 + 5N + 100이면 복잡도는 O(N^2)이라고 한다.
뭐 이거는 lim 개념이랑 비슷하다. 최고차항이외는 영향을 거의 안주기 때문이다.
입력 크기 N과 계산 단계 횟수의 상관관계
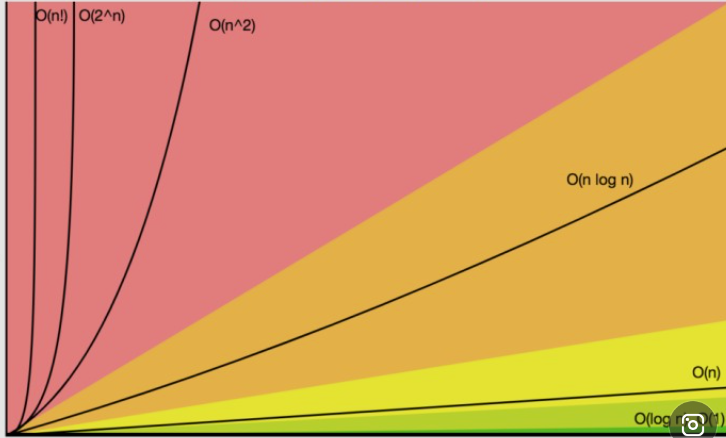
효율적인 코드를 위해 시간 복잡도 이해는 필수다.
O(log N^2) 을 O(NlogN)으로 바꿀 수만 있어도 엄청난 차이가 있으니 그런 부분을 생각하며 문제 해결 알고리즘을 결정하자.
연습 문제
난이도가 3개 정도되는 연습문제만 몇개 골라서 남기겠다.
2.5 나이 맞히기 게임에서 A씨 나이가 0세 이상 N세 미만일 때 이진 탐색법으로 O(logN)회에 맞힐 수 있다는 것을 증명하라.
마무리
생각보다 술술 읽히고 알았던 내용도 다시 정리할 수 있어서 좋았다. 더 나은 코드를 위해 끝까지 읽어봐야겠다.
:)