📌 그래프 - Graph
그래프에는 사실 아주 다양한 형태가 존재합니다.
우리가 일반적으로 사용하는 리스트가 그래프일수도있고 이번에 배울 트리 또한 그래프의 하나입니다.
트리를 배우기 전에 그래프가 무엇인지 자세히 알아보겠습니다.
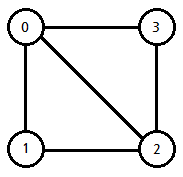
그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조입니다.
📕무방향 그래프 - Undirected Graph
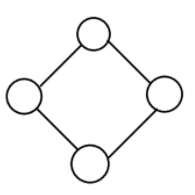
무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프를 의미합니다.
📙 방향 그래프 - Directed Graph
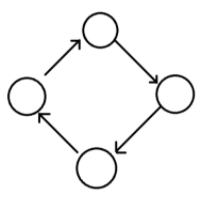
방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프입니다.
방향에 따라서만 이동할 수 있습니다.
📗 가중치 그래프 - Weighted Graph
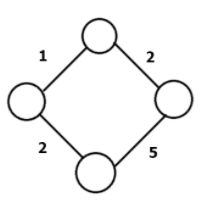
가중치 그래프는 간선에 가중치(비용)이 존재하는 그래프입니다.
두 정점을 이동할때 비용이 드는 그래프입니다.
다익스트라와 같은 알고리즘이 사용됩니다.
📘 연결 그래프 - Connected Graph
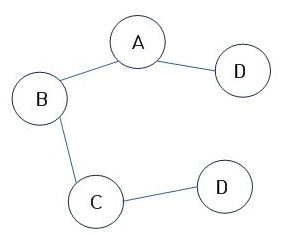
무방향 그래프에 있는 모든 정점들에 대해 경로가 존재하는 그래프입니다.
즉 노드들이 하나도 빠짐없이 간선에 연결되어있습니다.
📕 비연결 그래프 - Disconnected Graph
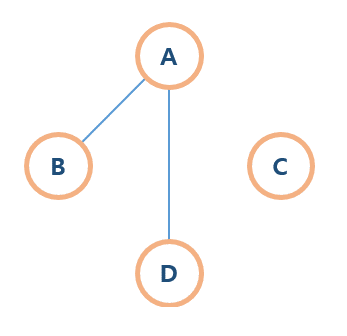
무방향 그래프에서 특정 정점 사이에 경로가 존재하지 않는 그래프입니다.
📙 완전 그래프 - Complete graph
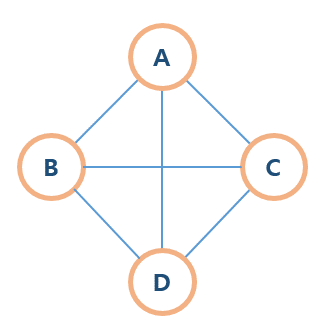
모든 정점이 서로 간선으로 연결되어있는 그래프입니다.
📗 순환 그래프 - Cycle graph
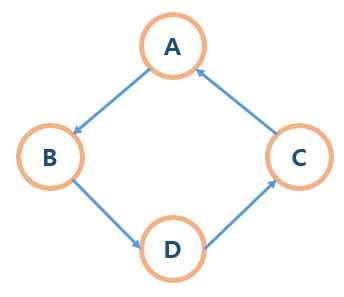
시작정점과 도착 정점이 동일한 그래프입니다. A 에서 이동하면 다시 A로 도착할 수 있습니다.
📘 비순환 그래프 - Acyclic graph
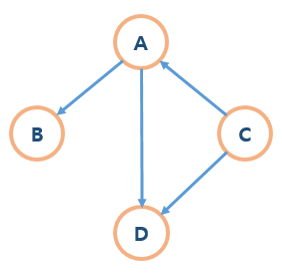
사이클이 없는 그래프 입니다.
📌 트리 - Directed Acyclic Graph
그래프의 종류를 알아봤으니 이제 트리에 대해 알아보겠습니다.
트리는 DAG 로 순환이 없는 방향 그래프입니다.
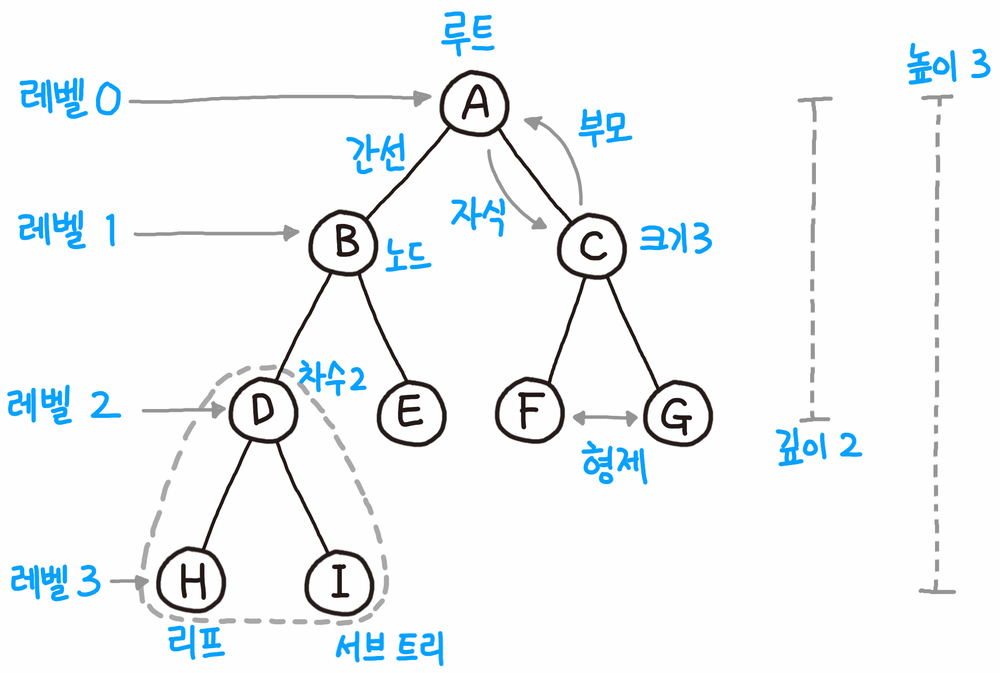
트리에서는 다양한 용어가 있습니다. 이는 중요하기 때문애 꼭 기억해야합니다.
| 용어 | 의미 |
|---|---|
| 루트 노드(Roof node) | 부모가 없는 최상위 노드 |
| 단말 노드(leaf node) | 자식이 없는 노드 |
| 크기 (size) | 트리에 포함된 모든 노드의 개수 |
| 깊이(depth) | 루트 노드로부터의 거리 |
| 높이 (height) | 깊이 중 최대값 |
| 차수 (defree) | 각 노드의 간선 개수 |
기본적으로 트리의 크기가 일때 , 전체 간선의 개수는 개 입니다.
위 그림에서 높이는 3이고 루트노드는 깊이가 0 입니다.
📌 이진탐색트리 - Binary Search Tree
이진탐색트리는 최소값 또는 최대값을 보다 효율적으로 탐색가능한 자료구조입니다.
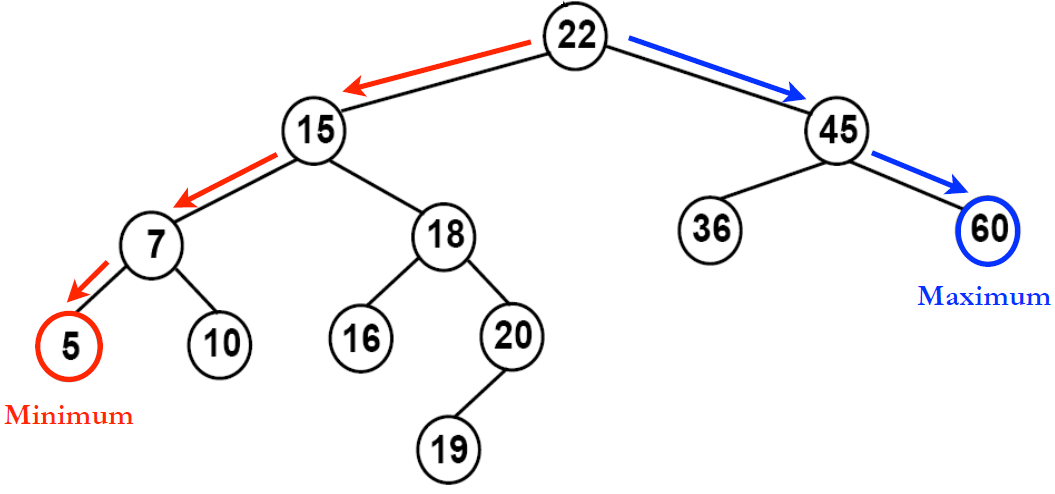
2가지 특징이 있습니다.
- 부모 노드보다 왼쪽 자식 노드가 값이 더 작다.
- 부모 노드보다 오른쪽 자신 노드가 값이 더 크다.
우선순위 큐에 사용됩니다.
특정 값을 찾고자 할때 현재 노드보다 값이 더 크면 오른쪽으로 , 현재노드보다 값이 더 작으면 왼쪽으로 탐색하면됩니다.
시간복잡도는 최소 이고 최대 의 시간복잡도가 듭니다.
📌 트리의 순회 - Tree Traversal
트리 순회는 트리 자료구조에 포함된 노드를 특정 방법으로 한번씩 방문하는 방법을 의미합니다.
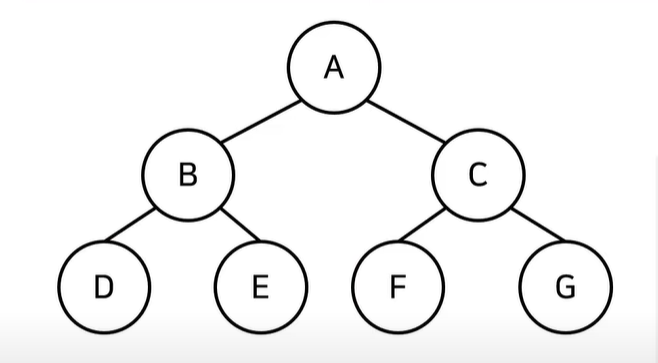
다음과 같은 트리에서 전위순회 , 중위순회 , 후위순회 탐색에 대해 알아보겠습니다.
📕 전위 순회 - Preorder traverse
전위순회는 루트노드를 먼저 탐색하고 왼쪽을 우선시 하여 탐색합니다.
따라서 A - B - D - E - C - F - G 로 탐색합니다.
📙 중위 순회 - Inorder traverse
중위순회는 왼쪽 하위루트를 방문후 루트를 방문합니다.
왼쪽 정점 -> 루트 -> 오른쪽 정점순으로 방문합니다.
따라서 D - B - E - A - F - C - G 로 탐색합니다.
📗 후위 순회 - Postorder traverse
후위순회는 하위 트리 모두 방문 후 루트노드를 방문합니다.
왼쪽 정점 -> 오른쪽 정점 -> 루트 노드 순으로 방문합니다.
따라서 D - E - B - F - G - C - A 순으로 탐색합니다.
📌 트리 순회 코드 구현
백준 1191번 : 트리 순회 문제를 통해서 파이썬으로 순회 코드를 작성하였습니다.
import sys
input=sys.stdin.readline
N=int(input())
tree={}
for i in range(N):
root,left,right=input().split()
tree[root]=[left,right]
def preorder(root):
if root!='.':
print(root,end='')
preorder(tree[root][0])
preorder(tree[root][1])
def inorder(root):
if root!='.':
inorder(tree[root][0])
print(root,end='')
inorder(tree[root][1])
def postorder(root):
if root!='.':
postorder(tree[root][0])
postorder(tree[root][1])
print(root,end='')
preorder('A')
print()
inorder('A')
print()
postorder('A')