백준 10723 : 판게아 1 (Python)

본문 링크

import sys
input=sys.stdin.readline

def Find(x):
    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])
    return disjoint[x]

T=int(input())
for i in range(T):

    N,M=map(int,input().split())

    edge=[]
    for j in range(N-1):
        a,b=map(int,input().split())
        edge.append((b, j+1,a)) #가중치 b , j+1 , a 가연결되어있음.

    check = []
    for j in range(M):

        disjoint=[ _ for _ in range(N+1) ]
        u,v,k=map(int,input().split())
        edge.append((k,u,v))

        edge.sort(key=lambda x:x[0]) ; total=0

        for value,x,y in edge:

            x=Find(x)
            y=Find(y)

            if x!=y:
                if x>y:
                    disjoint[x]=y
                else:
                    disjoint[y]=x
                total+=value

        check.append(total)

    answer=check[0]

    for k in range(1,len(check)):
        answer=answer^check[k]
    print(answer)

📌 어떻게 접근할 것인가?

이해하는데 좀 오래걸렸다. 문제 입력도 까다롭게 써놓았고 구하라는것도 애매하게 설명되어있다.

자세하게 알아보자.

일단 예제 입력부터 보자

• 1
  3 3
  0 5
  1 3
  0 2 4
  0 1 2
  0 0 2

첫번째 값 1 은 테스트 케이스 개수다.

두번째는 $N$ 와 $M$ 이 주어진다. 그리고 $N-1$ 줄에 이미 연결되어있는 도시를 주어진다.

지문에서는

• 이는 $i$ 번 도시와 $u_i$ 번 도시가 길이가 $c_i$ 인 도로로 연결되어 있다는 뜻이다.

라고 적혀있는데 , 이미 연결되어있는 도시만 보면

• 0 5
  1 3

이다. 첫번째 노드의 값은 입력받는 횟수 이고 입력받는 첫번째 값이 연결된 노드 , 마지막 값이 가중치이다. 입력받는 횟수는 1 번 부터 시작한다.

따라서 $1$ 과 $0$ 번 노드가 가중치 $5$ 로 연결되어있고 , $2$ 와 $1$ 번 노드가 가중치 $3$ 으로 연결되어있다는 뜻이다.

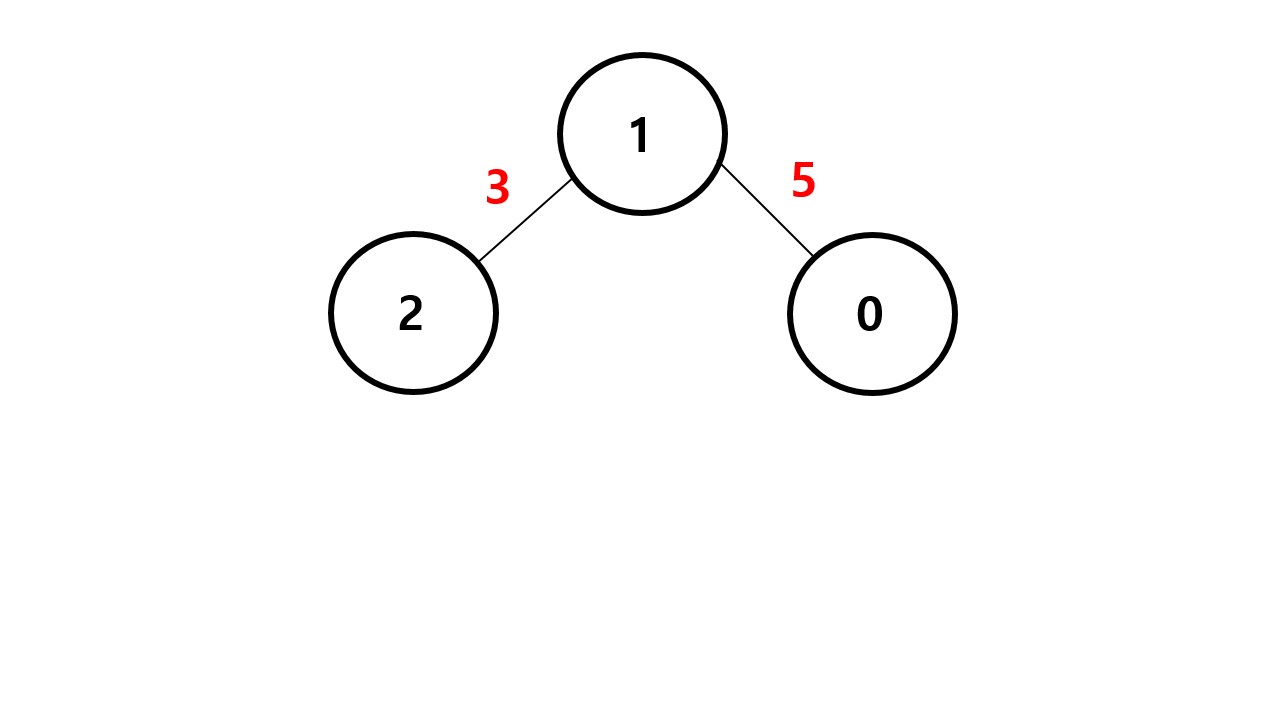
즉 위 그림과 동일하다.

이후 $M$ 줄의 걸쳐서 $u_j$ , $v_j$ , $c_j$ 가 주어지는데

간단하게 $u_j$ , $v_j$ 라는 두 노드가 가중치 $c_j$ 로 연결되어있다는 뜻이다.

이제 문제에서 구하고자 하는것을 살펴보자.

• 매번 도로가 추가되고 나면 모든 도로 중 일부를 선택하여 모든 도시가 서로 직간접적으로 연결되어 있도록 하며, 이때 선택된 도로들의 길이의 합을 최소로 하는 도로의 부분집합을 알아내기.

그냥 최소 스패닝 트리를 구하란 말이다. 문제 참 어렵게 만들어놨다.

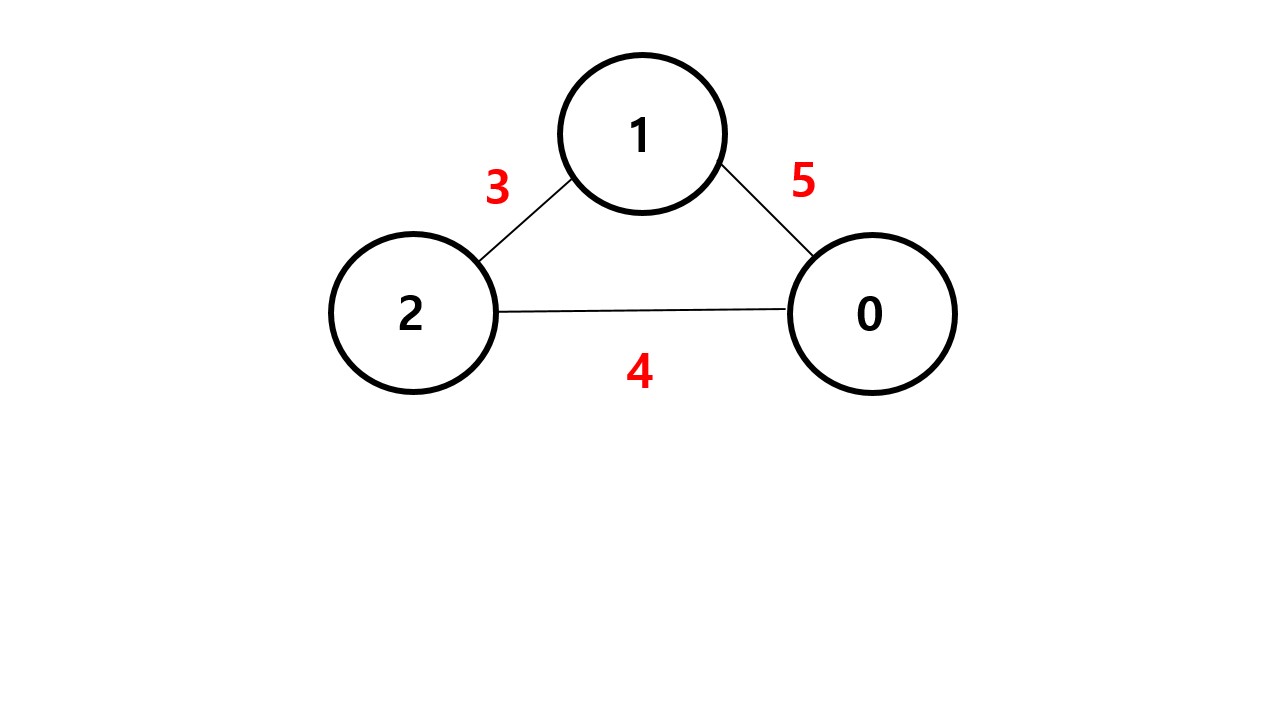
$M$ 개 줄에 걸쳐서 입력받을때 첫번째 입력값을 보자.

• 0 2 4

0 번 노드와 2번 노드를 가중치 4로 연결했다.

연결을 그대로 해버리면 사이클이 생긴다.
하지만 우리는 간선을 임의적으로 지울 수 있다.

따라서 간선이 5 인 값을 지우자.

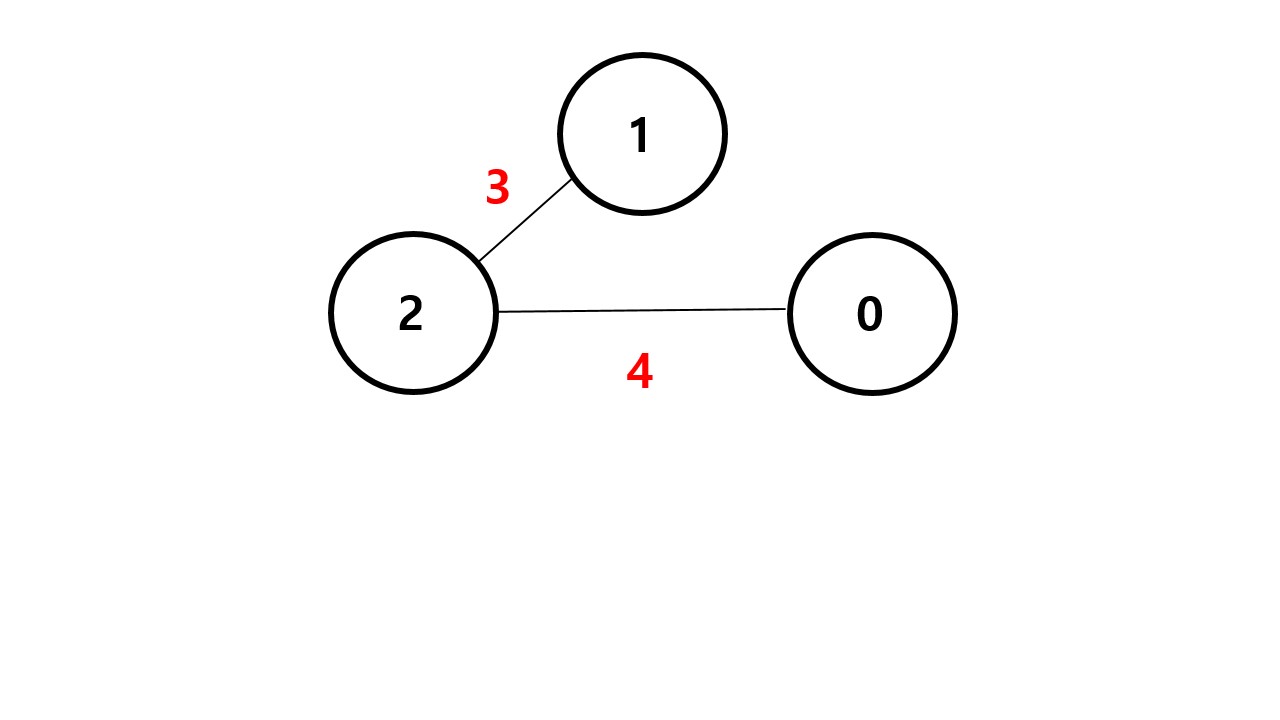
이렇게 지워도 스패닝 트리가 형성되며 , 최소 스패닝 트리이기 때문에 가장 가중치가 큰 간선을 지웠다.

현재 최소 스패닝 트리 값은 3+4 = 7 이다.

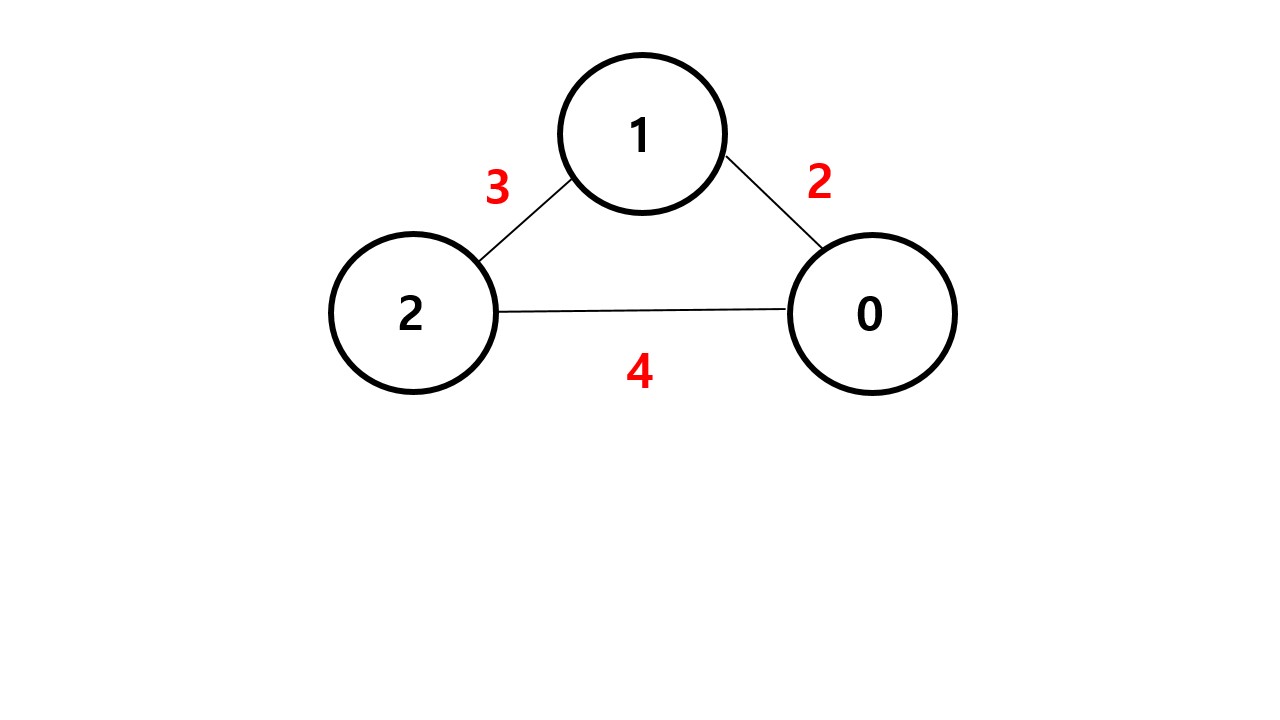
다음 입력값을 보자.

• 0 1 2

이전의 노드에서 0번 노드와 1번 노드를 가중치 2인 간선으로 연결했다.

이러면 또 사이클이 생긴다. 아까처럼 간선을 하나 지우도록 하자.

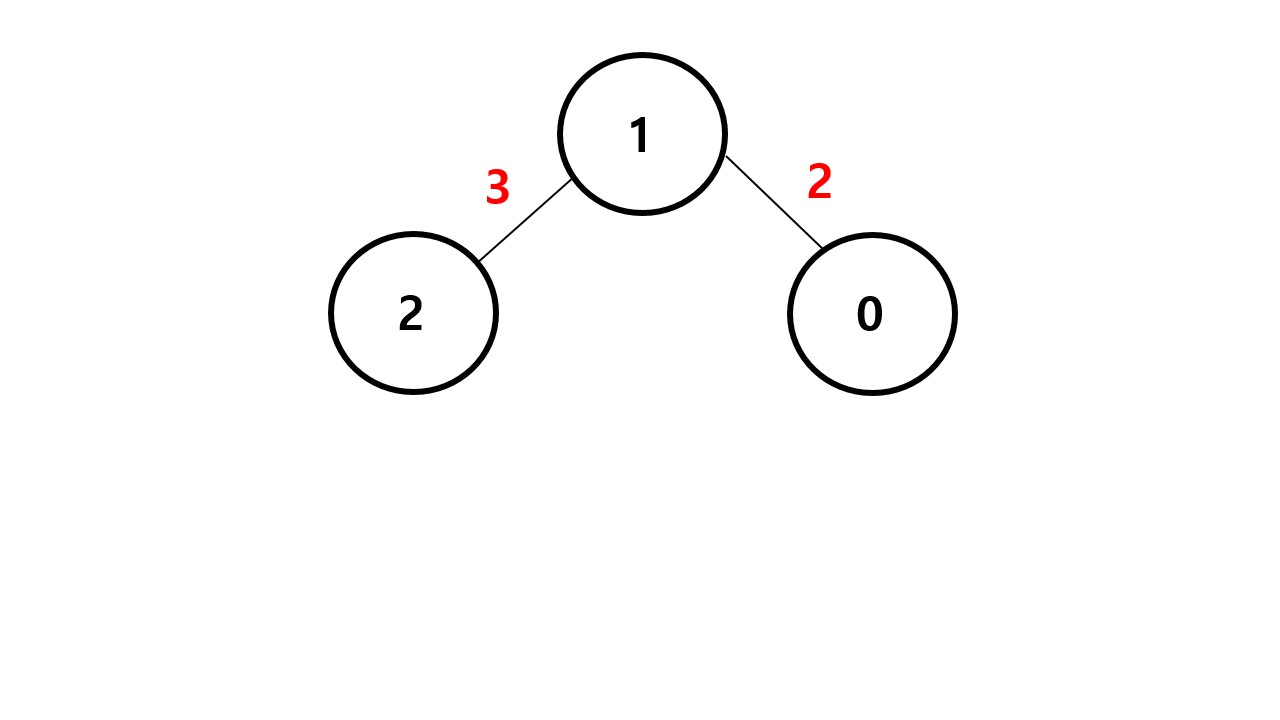
간선의 가중치가 가장 큰 4를 지웠다. 이제 최소 스패닝 트리를 만들었고 모든 가중치의 합은 3+2 = 5 이다.

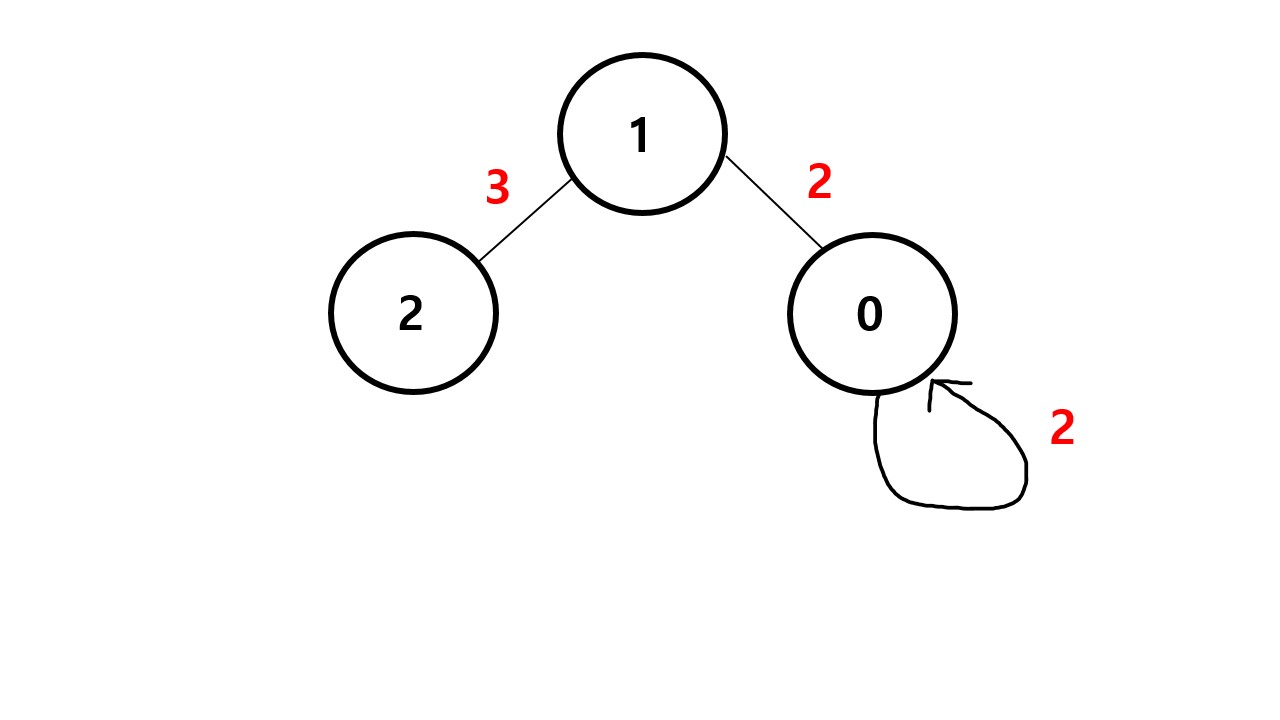
마지막 입력값은

• 0 0 2

이다. 지금은 최소 스패닝 트리를 구하기 때문에 굳이 자기자신을 가르키는 간선을 가질 필요가 없다.
오히려 값만 더 늘어나기 때문이다.
이것도 그냥 지워버린다.

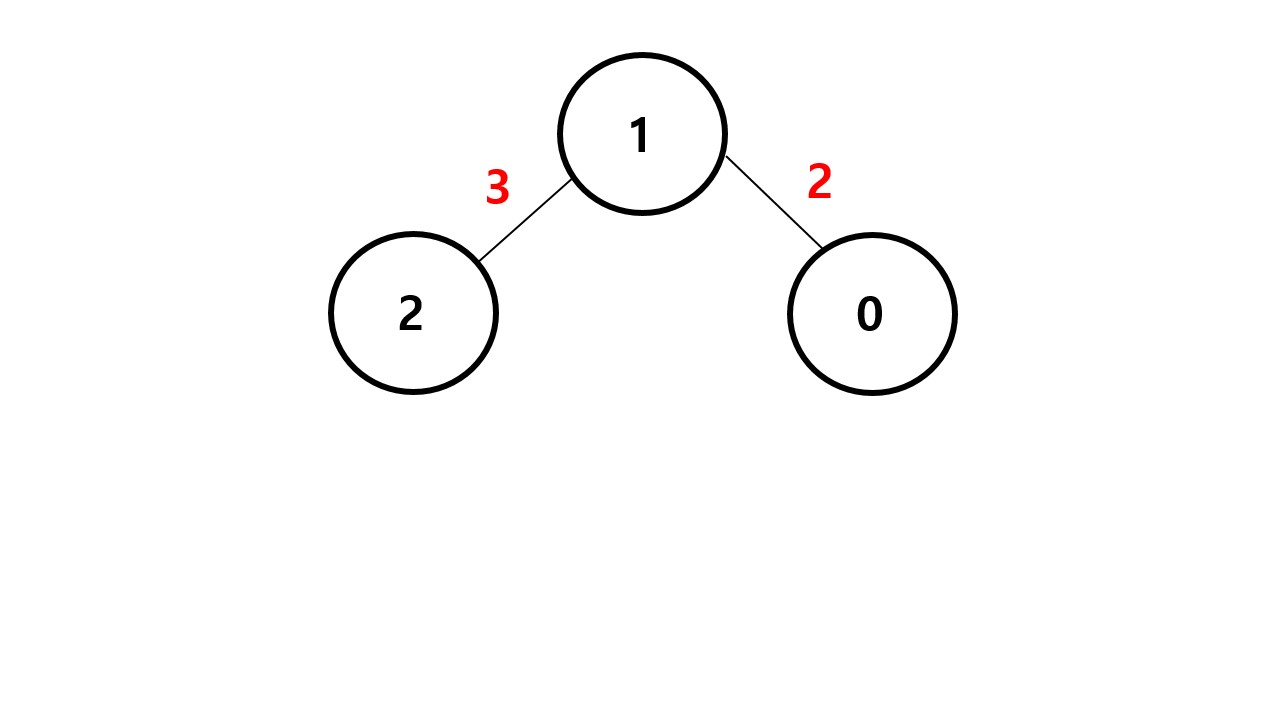
그래서 다시 가중치의 합이 5가 된다.

현재 구한 가중치의 값은 $[7 , 5, 5]$ 이다.

이후 $7$ , $5$ , $5$ 를 전부 $XOR$ 연산을 해주면 값이 $7$ 이 나온다.

크루스칼 알고리즘을 사용하였고 edge 라는 간선을 저장하는 리스트를 만들어서 $M$ 개의 줄에 걸쳐서 매번 간선이 추가될때마다 , 그때의 최소 스패닝 트리를 만들어 준 후에 최소 스패닝 트리 값을 저장한다.

이후 $M$ 번의 최소 스패닝 트리를 완성했다면 값을 저장한 리스트를 전부 $XOR$ 연산을 해주었다.