백준 11066 : 파일 합치기 (Python)

본문 링크

import sys
input=sys.stdin.readline

T=int(input())

for _ in range(T):
    K=int(input())

    L=list(map(int,input().split()))
    L.insert(0,0)
    dp=[ [0]*(K+1) for _ in range(K+1)]


    S=[0]*(K+1)
    for i in range(1,K+1):
        S[i]=S[i-1]+L[i]

    dp=[ [0]*(K+1) for i in range(K+1)]

    for i in range(2,K+1):
        for j in range(1,K+2-i):
            dp[j][j+i-1]=min(dp[j][j+p]+dp[j+p+1][j+i-1] for p in range(i-1))+(S[j+i-1]-S[j-1])
    print(dp[1][K])

T = int(input())

for _ in range(T):
    K = int(input())
    C = list(map(int, input().split()))
    dp = [[0]*(K+1) for _ in range(K+1)]
    # dp[i][j][u] = 파일 i개를 j 번째 부터 j+i-1번째 더했을 때 드는 비용의 최솟값
    sum_C = [0]
    for i in range(K):
        sum_C.append(sum_C[-1]+C[i])        
        
    for i in range(2,K+1): # 만들 파일의 개수 선택
        for j in range(1,K-i+2): # 파일의 시작 j번째 선택
            dp[i][j] = 99999999999999
            for p in range(1,i): # p개 + i-p개 중 p를 선택 (1 ~ i-1)
                dp[i][j] = min(dp[i][j], dp[p][j] + dp[i-p][j+p] + sum_C[j+i-1] - sum_C[j-1])
    #print(dp)
    print(dp[K][1])

📌 어떻게 접근할 것인가?

이 문제는 혼자못풀정도로 어려운 난이도였다. 이해하기도 굉장히 어렵기 때문에
문제에서 주는 예제를 통해 이해를 해보고자 한다.
예제 입력을 보자

• 입력
  4
  40 30 30 50
• 출력
  300

먼저 DP는 2차원 배열을 사용할 것이고,
DP[i][j]는 i에서 j까지 합하는데 필요한 최소 비용이 된다.

또한 배열을 효율적으로 계산하기 위해 누적합 배열을 만들어줘야한다.
누적합을 구해주면 다음과 같다. [0, 40, 70, 100, 150]

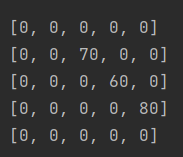
길이가 2일 경우,

(1,2), (2,3), (3,4) 파일로 나눌 수 있다. 실제로 계산해보면

• 1번부터 2번파일까지의 비용은 (1~1의 비용(0) + 2~2의 비용(0)) + (1~2까지 누적합(70)) = 70
• 2번부터 3번파일까지의 비용은 (2~2의 비용(0) + 3~3의 비용(0)) + (2~3까지 누적합(60)) = 60
• 3번부터 4번파일까지의 비용은 (3~3의 비용(0) + 4~4의 비용(0)) + (2~3까지 누적합(80)) = 80

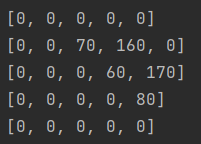
다음 길이가 3일 경우,

(1 + 2,3), (1,2 + 3), (2, + 3,4), (2,3 + 4) 파일로 나눌 수 있고

1번부터 3번파일까지의 비용은 min(1~1의 비용(0) + 2~3의 비용(60) , 1~2의 비용(70) + 3~3의 비용(0))

• (1~3까지의 누적합(100)) = 160 이 된다.

2번부터 4번파일까지의 비용은 min(2~2의 비용(0) + 3~4의 비용(80), 2~3의 비용(60) + 4~4의 비용(0))

• (2~4까지의 누적합(110)) = 170 이 된다.

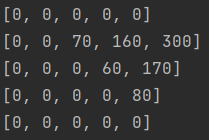
마지막으로 길이가 4일 경우,

(1 +,2,3,4), (1,2 + 3,4), (1,2,3 + 4) 파일로 나눌 수 있다.

1번부터 4번파일까지의 비용은 min(1~1의 비용(0) + 2~4의 비용(170), 1~2의 비용(70) + 3~4의 비용(80), 1~3의 비용(160) + 4~4의 비용(0))

• (1~4까지의 누적합(150)) = 300 이 된다.

여기서 찾을 수 있는 점화식은
DP[i][k] + DP[k+1][j] + sum(A[i]~A[j]) 이고
(i~k)까지 비용의 합과 그 다음 (k+1지점부터 마지막 지점)까지의 합의 최소에
(i~j)까지의 누적합을 더해주면 얻고자하는 해를 얻을 수 있다.

이후 DP[1][K]를 출력해주면 원하는 값이 나온다.