백준 16235 : 나무 제테크 (Python)

본문 링크

import sys
input=sys.stdin.readline
from collections import deque

LMI=lambda:list(map(int,input().split()))
MI=lambda:map(int,input().split())
I=lambda:int(input())
G=lambda x:[ LMI() for _ in range(x) ]
V=lambda x,y:[ [False]*y for _ in range(x) ]

"""
봄에는 나무가 자신의 나이만큼 양분을 먹고, 나이가 1 증가한다. 
각각의 나무는 나무가 있는 1×1 크기의 칸에 있는 양분만 먹을 수 있다. 
하나의 칸에 여러 개의 나무가 있다면, 나이가 어린 나무부터 양분을 먹는다. 
만약, 땅에 양분이 부족해 자신의 나이만큼 양분을 먹을 수 없는 나무는 양분을 먹지 못하고 즉시 죽는다.
"""
def Spring():
    dead.clear()
    for i in range(N):
        for j in range(N):
            idx=0
            for k in range(len(tree[i][j])):
                if ground[i][j]>=tree[i][j][k]:
                    ground[i][j]-=tree[i][j][k]
                    tree[i][j][k]+=1
                    idx+=1
                else:
                    break

            for k in range(len(tree[i][j])-idx):
                ground[i][j]+=tree[i][j][-1]//2
                tree[i][j].pop()

"""
여름에는 봄에 죽은 나무가 양분으로 변하게 된다. 
각각의 죽은 나무마다 나이를 2로 나눈 값이 나무가 있던 칸에 양분으로 추가된다. 소수점 아래는 버린다.
"""

"""
가을에는 나무가 번식한다. 
번식하는 나무는 나이가 5의 배수이어야 하며, 인접한 8개의 칸에 나이가 1인 나무가 생긴다.
상도의 땅을 벗어나는 칸에는 나무가 생기지 않는다.
"""

def Fall():
    P=[]
    for i in range(N):
        for j in range(N):
            for k in range(len(tree[i][j])):
                if tree[i][j][k]%5==0:
                    for _ in range(8):
                        nx,ny=i+dx[_],j+dy[_]
                        if 0<=nx<N and 0<=ny<N:
                            P.append((nx,ny))

    for x,y in P:
        tree[x][y].appendleft(1)

"""
겨울에는 S2D2가 땅을 돌아다니면서 땅에 양분을 추가한다. 
각 칸에 추가되는 양분의 양은 A[r][c]이고, 입력으로 주어진다.
"""
def Winter():
    for i in range(N):
        for j in range(N):
            ground[i][j] += graph[i][j]

def Alive():
    total=0
    for i in range(N):
        for j in range(N):
            total+=len(tree[i][j])
    return total

dx=[-1,1,0,0,-1,-1,1,1]
dy=[0,0,-1,1,-1,1,-1,1]
N,M,K=MI()
graph=G(N)
tree=[ [ deque() for _ in range(N)] for _ in range(N)]
dead=[]
for i in range(M):
    x,y,z=MI()
    tree[x-1][y-1].append(z)
ground=[ [5]*N for _ in range(N) ] #가장 처음에 양분은 모든 칸에 5만큼 들어있다.

for i in range(K):
    Spring()
    Fall()
    Winter()
print(Alive())

📌 어떻게 풀 것인가?

구현자체는 굉장히 쉬운문제입니다. 다만 코드의 효율성을 극한으로 끌어올려야합니다. python,java 언어라면 자칫하면 시간초과받기 쉬운문제입니다.

일단 나무를 담을 배열을 저는 from collections import defaultdict 라이브러리를 통해 딕셔너리를 사용했습니다. 좌표값에 해당하는 나무를 담았습니다.

하지만 defaultdict 보단 리스트가 속도가 빠릅니다.

import time
from collections import defaultdict
from collections import deque
def list_append():
    target = deque()
    for i in range(10**6):
        target.append(i)
    return target

def dict_input():
    target = defaultdict(deque)
    for i in range(10**6):
        target[i].append(i)

    return target

start= time.time()

list_append()

end= time.time()

print("%.5f"%(end-start))

실험을 해보겠습니다.

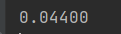
단순히 deque 를 append 를 $10^6$ 번 할시 0.044 초가 걸립니다.

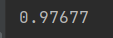
하지만 dict_input() 함수를 호출하면 0.97초나 걸립니다.

dx=[-1,1,0,0,-1,-1,1,1]
dy=[0,0,-1,1,-1,1,-1,1]
N,M,K=MI()
graph=G(N)
tree=[ [ deque() for _ in range(N)] for _ in range(N)]
dead=[]
for i in range(M):
    x,y,z=MI()
    tree[x-1][y-1].append(z)
ground=[ [5]*N for _ in range(N) ] #가장 처음에 양분은 모든 칸에 5만큼 들어있다.

다시 본문 코드를 봅시다. dx,dy 는 8방향을 나타냅니다.

이후 tree 는 3차원 deque 배열로 만들어 주었습니다. 이후 $M$ 번 동안 나무를 입력받습니다. 이때 좌표값은 모두 1 을 빼줘야합니다. ground 는 실제 양분이 담겨있는 땅을 의미하며 초기값은 전체 5 입니다.

def Spring():
    dead.clear()
    for i in range(N):
        for j in range(N):
            idx=0
            for k in range(len(tree[i][j])):
                if ground[i][j]>=tree[i][j][k]:
                    ground[i][j]-=tree[i][j][k]
                    tree[i][j][k]+=1
                    idx+=1
                else:
                    break

            for k in range(len(tree[i][j])-idx):
                ground[i][j]+=tree[i][j][-1]//2
                tree[i][j].pop()

봄입니다. 3중 반복문을 통해서 나무를 땅에 심을 수 있는지 판별합니다. 이후 땅을 심을 수 없으면 그떄의 인덱스 값을 idx 에 담고 나머지 부분은 어짜피 여름일때 ground 배열에 양분이 되므로 ground 배열에 값을 더해줌과 동시에 pop 을 사용해서 원소를 삭제해줍니다.

def Fall():
    P=[]
    for i in range(N):
        for j in range(N):
            for k in range(len(tree[i][j])):
                if tree[i][j][k]%5==0:
                    for _ in range(8):
                        nx,ny=i+dx[_],j+dy[_]
                        if 0<=nx<N and 0<=ny<N:
                            P.append((nx,ny))

    for x,y in P:
        tree[x][y].appendleft(1)

가을입니다.
이전에 봄에서 else 문을 통해 break 를 해주었습니다. 하지만 문제에서는 나이가 적은 나무부터 양분을 먹어야 하기 때문에 원래라면 sort 를 사용해서 정렬을 해주어야 합니다. 하지만 appendleft 를 사용해서 새로 심을 나무의 나이는 1 이므로 tree 에 가장 왼쪽에 원소를 넣어줌으로써 오름차순을 자동으로 만들어 줍니다.

따라서 sort 를 사용하지 않음으로써 시간복잡도를 줄일 수 있습니다.

def Winter():
    for i in range(N):
        for j in range(N):
            ground[i][j] += graph[i][j]

겨울일때는 입력때 받은 graph 값을 ground 배열에 담아줍니다.

def Alive():
    total=0
    for i in range(N):
        for j in range(N):
            total+=len(tree[i][j])
    return total

살아남은 나무의 개수를 확인하는 함수입니다.

for i in range(K):
    Spring()
    Fall()
    Winter()
print(Alive())

따라서 총 $K$ 번 동안 세개의 함수를 실행해주고 마지막에 Alive() 함수를 실행해줍니다.

구현자체는 쉽지만 적절한 자료형의 선택과 정렬을 하지 않는 방법 등 아이디어가 까다로웠던 문제였었습니다.