백준 16437 : 양 구출 작전 (Python)

본문 링크

import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

N=int(input())
Tree=[ [] for _ in range(N+1) ]
dp=[ [0,0] , [0,0] ]
for i in range(N-1):
    t,a,p=input().split()
    Tree[int(p)].append(i+2)
    dp.append([t,int(a)])

def DFS(Node):
    result=0

    for i in Tree[Node]:
        result+=DFS(i)

    if dp[Node][0]=="W": #늑대라면
        result=max(0,result-dp[Node][1])
    else:
        result+=dp[Node][1]
    return result

print(DFS(1))

📌 어떻게 접근할 것인가?

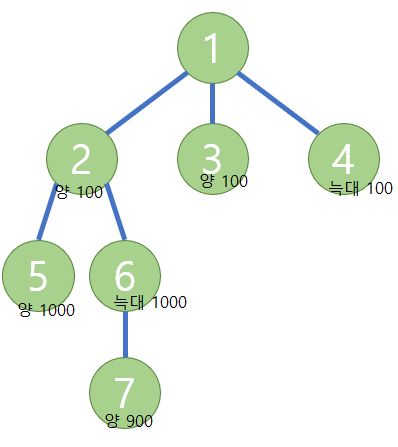
예제 2번을 보자.
노드 5 - 2 - 1 로 올라가서 1100이 추가되고
노드 3 - 1 로 올라가서 100이 추가된다.

이때 노드 4 -1 에서 올라갈때는 늑대가 올라갈 필요는없으며
노드 7 - 6 으로 올라갈때 양은 늑대에게 전부 잡히므로 0 이 된다.

즉 이 문제는 리프노드부터 루트노드까지 역으로 탐색해야 한다.

✅ Code

일단 입력받을때 루트번호가 1 이므로 첫 입력의 노드는 2가 된다.

Tree=[ [] for _ in range(N+1) ]
dp=[ [0,0] , [0,0] ]

for i in range(N-1):
    t,a,p=input().split()
    Tree[int(p)].append(i+2)
    dp.append([t,int(a)])

따라서 다음과 같이 입력받아야 한다. dp 리스트에는 늑대인지 양인지를 저장하는 $t$ 값과 그떄의 양 $a$ 값을 저장한다.
이때 주의해야할 점은 인덱스가 2부터 시작하기 때문에 dp 배열에 $[0,0]$ 을 2개 넣어주어야 한다.

def DFS(Node):
    result=0

    for i in Tree[Node]:
        result+=DFS(i)

    if dp[Node][0]=="W": #늑대라면
        result=max(0,result-dp[Node][1])
    else:
        result+=dp[Node][1]
    return result

가장 중요한 $DFS$ 탐색 부분이다. 루트노드는 항상 $1$ 이기 때문에 $DFS(1)$ 을 호출하면 된다.

result 에 $Tree$ 를 탐색한 값을 추가해준다.

이때 함수 자체를 더하면 함수의 끝까지 재귀탐색을 하고 더한다.

따라서 리프노드에 도착했을때 dp 값이 늑대인지 양인지에 따라 리프노드부터 $return$ 을 해서
점점 값을 위로 올려보내는 식으로 result 값이 증가한다.

즉 5번노드에 있는 양을 2번노드로 올려보내고 , 7번노드의 양을 6번노드로 올린다고 생각하면 편하다. 따라서 문제에서 요구하는 원리와 똑같이 구현된다.

이때 주의해야할 점은 result 는 전역변수가 아니라 지역변수로 선언해줘야 한다.