백준 1707 : 이분 그래프 (Python)

본문 링크

import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

def DFS(start,group):
    global check

    if not check: #사이클이 존재한다면 탈출
        return

    visit[start]=group #해당 그룹으로 등록

    for i in graph[start]:
        if not visit[i]:
            DFS(i,-group)  # 탐색하지 않은 지점이라면 다른그룹 지정

        elif visit[i]==visit[start]: # 인접한 지점이면서 같은 그룹이면 이분그래프가 아님.
            check=False
            return

for i in range(int(input())):
    V,E=map(int,input().split())

    graph=[ [] for _ in range(V+1)]
    visit=[False]*(V+1)

    check=True

    for j in range(E): #무방향 그래프이기 때문에 원소룰 2번 추가해줘야함.
        a,b=map(int,input().split())
        graph[a].append(b)
        graph[b].append(a)

    for i in range(1,V+1):

        if not visit[i]: #방문하지 않은 지점이라면 방문처리
            DFS(i,1)
        if not check: #check 가 False이라면 이분그래프가 아님.
            break

    if not check:
        print("NO")
    else:
        print("YES")

📌 어떻게 접근할 것인가?

이분 그래프 판별 문제이다.

AtCoder Beginner Contest 282 에도 이분그래프 문제가 나와서 이분 그래프 기초 문제를 풀었다.

일단 이분그래프가 무엇인지 부터 살펴보자.

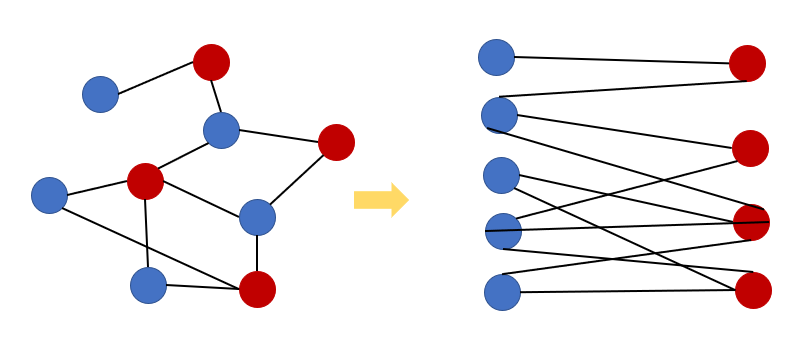
이분 그래프는 인접한 정점들이 현재 정점과 색깔이 다르게 칠해서 모든 정점을 2가지의 색으로 칠할 수 있는 그래프이다.

그렇다면 이분그래프인것을 어떻게 판별할까?
간단하다. 정점을 한가지 색깔로 칠한 후에 인접한 정점들을 다른 색으로 칠한다.
이때 만약 인접한 정점들중에 현재 정점과 색깔이 같은 정점이 있다면 이분그래프가 아니다.

$BFS$ , $DFS$ 모두 구현가능하지만 $DFS$ 로 구현하였다.

📌 Code

먼저 $graph$ 와 visit 를 간선의 개수+1 만큼 만들어준다.
check 변수가 $True$ 일때는 이분그래프 , $False$ 일때는 이분그래프가 아님을 나타낸다.

간선의 개수만큼 $graph$ 에 서로 연결된 정점을 추가해준다.
이때 무방향 그래프이기 때문에 원소룰 $2$번 추가해줘야한다.

이후 반복문을 통해 탐색하지 않은 지점에 대해 모두 탐색을 해준다.

$DFS$ 에서 탐색하지 않은 인접한 정점이 존재한다면 $-group$ 를 넣어서 다른 그룹으로 지정해준다.

만약 탐색을 했으면서 , 탐색한 지점과 현재 지점의 값(그룹) 이 같다면
check 변수를 $False$ 로 바꿔주고 함수를 종료한다.

이후 모든 정점들에 대해 탐색한 후에 check 값에 따라 $YES$ 또는 $NO$ 를 출력한다.