백준 17353 : 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별 (Java)

본문 링크

📌 사용 알고리즘 : Segment tree , 2차원 lazy Propagation

문제에서 원하는 쿼리는 다음과 같다.

• 1 $L$ $R$: [$L$, $R$]에 별이 떨어진다. (1 ≤ $L$ ≤ $R$ ≤ $N$)
• 2 $X$: 점 X에 떨어진 별의 개수의 합을 출력한다. (1 ≤ $X$ ≤ $N$)

2번 쿼리는 세그먼트 트리를 사용하면 바로 구할 수 있다.

1번 쿼리를 보자면 구간 업데이트 이므로 lazy propagation 을 사용하였다. 구간 업데이트를 하기 위해 매번 point update 시 $O(NQlogN)$ 의 시간복잡도가 필요하다.

그렇다면 lazy 에 어떤 값과 정보를 담을것인가?

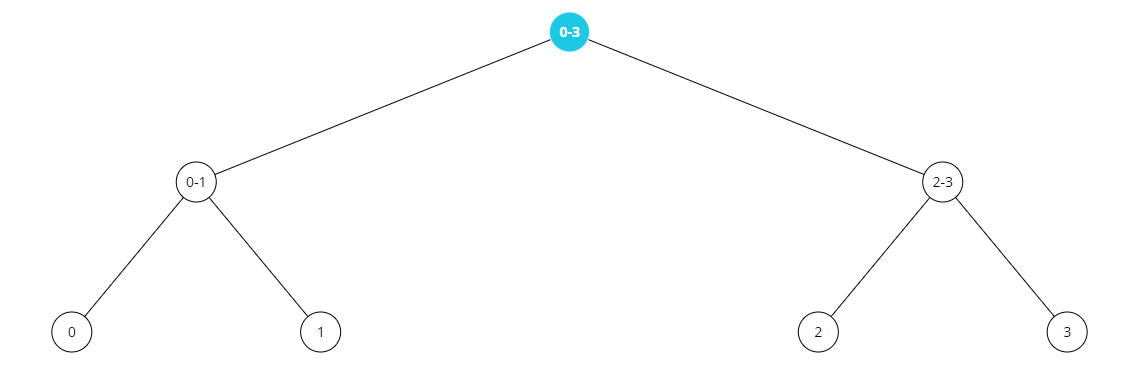
노드의 개수가 4개인 트리를 생각해보자. 이때 0~3 구간에 업데이트를 할때 lazy 는 왼쪽의 0~1 구간과 오른쪽의 2~3 값을 전파한다.

또한 구간의 범위를 자세히 보자. 0~1 구간은 0번노드와 1번노드 , 2~3구간은 2번노드와 3번노드를 저장한다.

lazy 를 전파할때 왼쪽 자식에는 특정 값을 더한다는 정보와 오른쪽 자식에는 특정 값을 전파하는 정보를 담으면 어떨까?

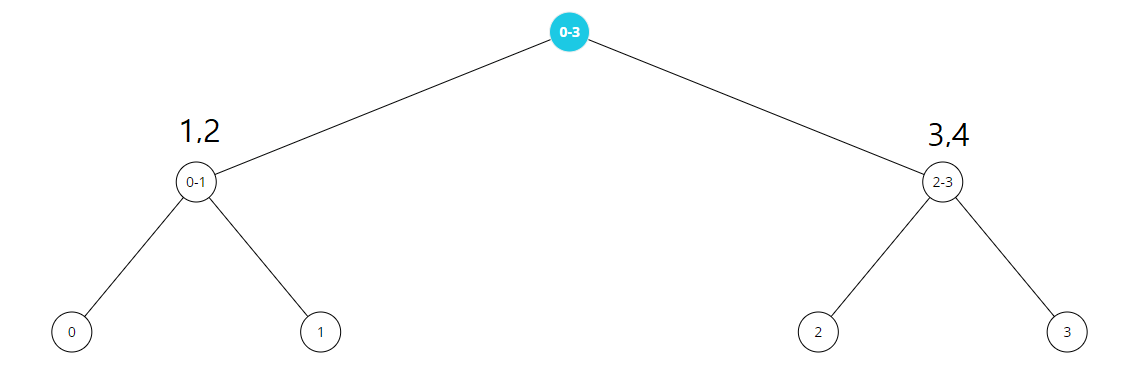
lazy 에 0~1구간은 1,2 라는 정보를 넣고 , 2~3구간에 3,4라는 정보를 저장하자.
그러면 lazy 를 통해 자식에 어떤 값을 저장할지를 알 수 있게된다.

하지만 여기서 또 문제가 생긴다. 구간의 범위가 2개 이상이라면? lazy 에 2개 이상의 정보를 매번 넣어줄 수 없다. 시간과 공간복잡도가 크게 늘어나기 때문이다.

2번 노드에 3 이라는 값을 준다는것을 어떻게 바로 알 수 있을까?

바로 0~1 구간의 크기와 쿼리에서 주어지는 $L$ , $R$ 을 통해 알 수 있다.

$L$ 이 0 이고 $R$ 이 3일때 , 2~3 구간에서 더해야할 시작값 은 $L$ - 구간의 시작값 + 1 이다.

void update(int start , int end , int left , int right) {
	lazy[node] += start-left+1; // 시작값
}

이런 코드를 작성할 수 있다.

몇번 시뮬레이션을 돌려보면 lazy 의 왼쪽 자식에는 항상 start-left+1 값을 전파해도 무방하다.

start-left+1 을 시작값이라고 부르자.

그렇다면 오른쪽 노드에는 값을 얼마를 주어야할까?
바로 시작값 + 왼쪽 트리의 크기 를 주면된다.

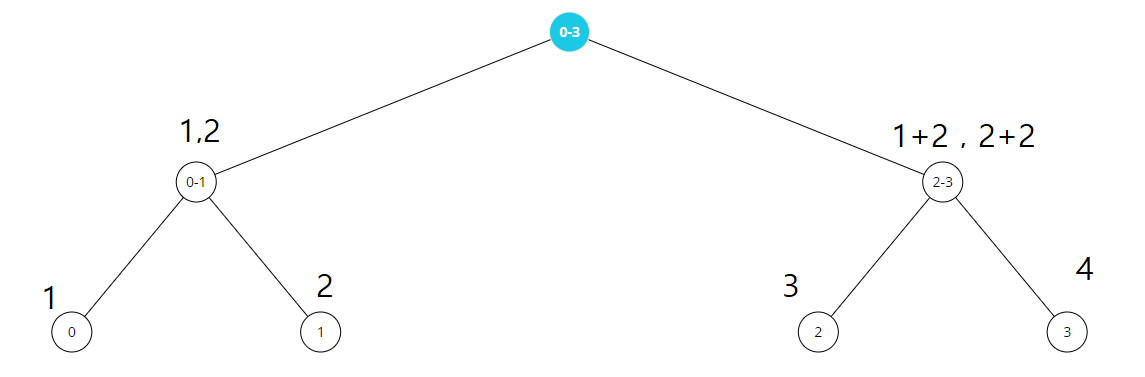
이런식으로 생각할 수 있다.

시작값은 항상 start-left+1 값을 통해 $O(1)$ 의 시간복잡도로 알 수 있다.

이제 왼쪽자식에게는 시작값 , 오른쪽 자식에게는 시작값 + 왼쪽트리의 크기를 lazy 로 전파한다면 리프노드에 값을 적절하게 넣을 수 있다.

하지만 이번에도 한가지 문제가 생긴다.

void update(int start , int end , int left , int right) {
	int mid = (start+end)>>1;
	lazy[node<<1] += start-left+1; // 시작값
    lazy[node<<1|1] += start-left+1 +  (mid-start+1)  ; // 왼쪽자식의 시작값 + 왼쪽자식의 구간크기
}

1 차원 lazy 를 사용했을때 lazy 에게 시작값 정보만 담는다고 해보자.

그리고 lazy 를 update 할때는 단순히 왼쪽자식에게 한번 , 오른쪽 자식에게 한번 값을 더해주기만 한다.

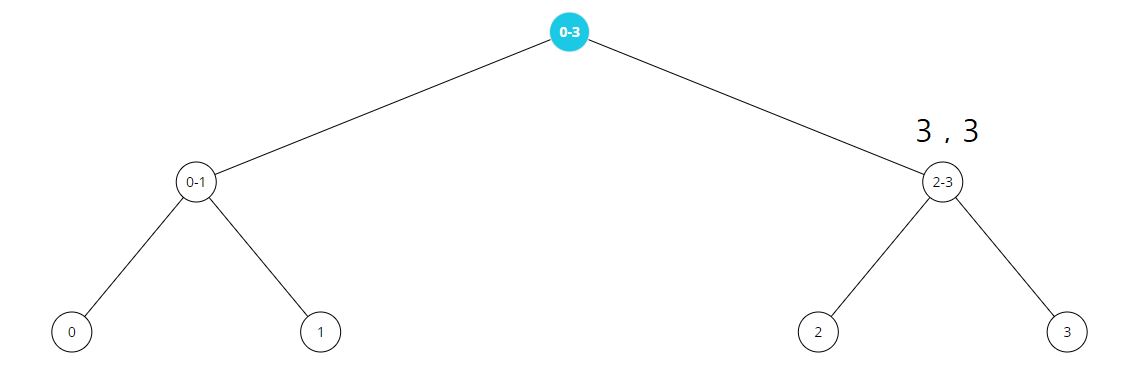
1차원 lazy 를 사용했을때 , 시작값만 담는다면 4개의 노드가 있는 segment tree 에서
전체 구간을 두 번 업데이트 한다고 가정해보자.

그러면 2~3 구간을 담당하는 lazy 는 3+3 = 6 이된다.
그런데 노드 3번에 값을 전파할때

void lazy_update(int node , int start , int end)
{
	int mid = (start+end)>>1;
    
    if (lazy[node]!=0)
    {
        tree[node]+=lazy[node];
        
        if (start!=end)
        {
            lazy[node<<1]+=lazy[node]; // 왼쪽 자식에는 현재 노드의 값을 전파한다.
            lazy[node<<1|1]+=lazy[node] + (mid-start+1); // 왼쪽 자식 트리의 크기
        }

        lazy[node]=0;
    }
}

위 처럼 lazyUpdate 코드를 작성할시 2~3 구간에서 왼쪽 자식의 크기는 1 이므로 오른쪽 자식에게 7 이라는 값을 더해주게 된다.

하지만 원래대로라면 전체구간을 0~3 구간에 1,2,3,4 를 두번 더해주면 3번노드는 값이 8 이 된다.

이런 현상이 왜 발생할까?
원래는 오른쪽 자식에게 왼쪽자식 트리의 크기를 매번 더해줘야 하지만
lazy 는 1차원 배열로 사용했고 왼쪽자식에게 전파할 값만 저장하기 때문에
오른쪽자식에게 매번 왼쪽자식 트리의 크기를 더한다는 정보를 저장하지 못한다.

long[][] lazy = new long[size][2]; 

따라서 2차원 lazy 를 사용해보자.
lazy[node][0] 은 왼쪽자식에 저장할 값과 lazy[node][1] 에는 구간을 더한 횟수를 저장했다.

구간을 더한 횟수를 저장한다면 오른쪽 자식에 전파할때 왼쪽자식크기×횟수 를 추가해주면 된다.

private long getRange(long range) {
    return range * (range + 1) / 2; // 1부터 range 까지의 합.
}

void update(int node , int start , int end , int left , int right) {

    lazyUpdate(node , start , end);

    if (left>end || right<start) {
        return;
    }
    int mid = (start+end)>>1;
    if (left<=start && right>=end) {

        tree[node] += getRange(end-left+1) - getRange(start-left);
        if (start!=end) {
            lazy[node<<1][0] += start-left+1; // 왼쪽 자식에게는 시작값
            lazy[node<<1|1][0] += start-left+1 +  (mid-start+1)  ; // 시작값 + 왼쪽자식의 구간크기
            lazy[node<<1][1]++;
            lazy[node<<1|1][1]++;
        }
        return;
    }
    update(node<<1 , start , mid , left , right);
    update(node<<1|1  , mid+1 , end , left , right);
    tree[node] = tree[node<<1] + tree[node<<1|1];
}

따라서 update 함수는 위처럼 작성할수있다.
참고로 1부터 $N$ 까지의 합 공식을 통해 tree[node] += getRange(end-left+1) - getRange(start-left) 으로 구간합을 바로 구할수있다.

void lazyUpdate(int node , int start , int end) {

    int mid = (start+end)>>1;

    if (lazy[node][0]!=0) {
        tree[node] += lazy[node][0];
        if (start!=end) {
            lazy[node<<1][0] += lazy[node][0];
            lazy[node<<1][1] += lazy[node][1];

            lazy[node<<1|1][0] += lazy[node][0] + (mid-start+1)*lazy[node][1];
            lazy[node<<1|1][1] += lazy[node][1];
        }
        lazy[node][0] = 0;
        lazy[node][1] = 0;
    }
}

lazy 전파 함수에서는 노드의 값과 구간을 더한 횟수를 전파해준다.
다만 이때 오른쪽 노드에서는 추가로 왼쪽자식트리의 크기 × 더한 횟수를 더해준다.

📌 전체 코드

import static java.lang.Integer.*;
import java.io.*;
import java.util.*;

class Segment {
    long[] tree  , arr;
    int size;
    long[][] lazy;

    public Segment(int size , long[] arr) {
        this.size = size;
        tree = new long[size];
        lazy = new long[size][2];
        this.arr = arr;
    }

    void init(int node , int start , int end) {
        if (start==end) {
            tree[node] = arr[start];
            return;
        }

        int mid = (start+end)>>1;
        init(node<<1 , start , mid);
        init(node<<1|1  , mid+1 , end);
        tree[node] = tree[node<<1] + tree[node<<1|1];
    }

    void lazyUpdate(int node , int start , int end) {

        int mid = (start+end)>>1;

        if (lazy[node][0]!=0) {
            tree[node] += lazy[node][0];
            if (start!=end) {
                lazy[node<<1][0] += lazy[node][0];
                lazy[node<<1][1] += lazy[node][1];

                lazy[node<<1|1][0] += lazy[node][0] + (mid-start+1)*lazy[node][1];
                lazy[node<<1|1][1] += lazy[node][1];
            }
            lazy[node][0] = 0;
            lazy[node][1] = 0;
        }
    }

    private long getRange(long range) {
        return range * (range + 1) / 2; // 1부터 range 까지의 합.
    }

    void update(int node , int start , int end , int left , int right) {

        lazyUpdate(node , start , end);

        if (left>end || right<start) {
            return;
        }
        int mid = (start+end)>>1;
        if (left<=start && right>=end) {

            tree[node] += getRange(end-left+1) - getRange(start-left);
            if (start!=end) {
                lazy[node<<1][0] += start-left+1; // 왼쪽 자식에게는 시작값
                lazy[node<<1|1][0] += start-left+1 +  (mid-start+1)  ; // 오른쪽자식에게도 시작값. 단 왼쪽자식의 시작값 + 왼쪽자식의 구간크기
                lazy[node<<1][1]++;
                lazy[node<<1|1][1]++;
            }
            return;
        }
        update(node<<1 , start , mid , left , right);
        update(node<<1|1  , mid+1 , end , left , right);
        tree[node] = tree[node<<1] + tree[node<<1|1];
    }

    long query(int node , int start , int end , int index) { // point query
        lazyUpdate(node , start , end);

        if (index>end || index<start) {
            return 0;
        }

        int mid = (start+end)>>1;

        if (start==end) {
            return tree[node];
        }

        return Math.max( query(node<<1 , start , mid , index) , query(node<<1|1 , mid+1 , end , index) );
    }
}
public class Main {
    static int index;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        int N , Q , query , left ,right ;
        long[] arr;

        N = parseInt(br.readLine());

        arr = new long[N + 1];

        st = new StringTokenizer(br.readLine());
        for (int i = 1 ; i <= N ; i++)  {
            arr[i] = Long.parseLong(st.nextToken());
        }

        Segment segment = new Segment(4*N , arr);

        segment.init(1 , 1 , N);

        Q = parseInt(br.readLine());

        while (Q-->0) {
            st = new StringTokenizer(br.readLine());
            query = parseInt(st.nextToken());
            if (query == 1) {
                left = parseInt(st.nextToken());
                right = parseInt(st.nextToken());
                segment.update(1, 1 , N , left , right);
            } else {
                index = parseInt(st.nextToken());
                bw.write(Long.toString(segment.query(1,1,N,index))+'\n');
            }

        }

        bw.flush();
    }
}

📌 후기

3일정도 고민하다가 겨우 자력솔한 문제다. 개인적으로 세그먼트 트리 응용문제중에 가장 좋았던 문제인거같다.

lazy 를 사용하는 법 말고 펜윅을 사용하거나 imos 기법을 사용한 풀이도 있다.

Lazy 없는 풀이 도 존재한다.