백준 1833 : 고속철도 설계하기 (Python)

본문 링크

import sys
input=sys.stdin.readline

def Find(x):

    if x!=disjoint[x]:
        disjoint[x]=Find(disjoint[x])

    return disjoint[x]
N=int(input())

graph=[ list(map(int,input().split())) for _ in range(N) ]

edge=[] ; disjoint=[ _ for _ in range(N+1) ] ; already=[] ; total=0 ; check=[]

for i in range(N):
    for j in range(N):
        if i==j:
            continue

        if graph[i][j]<0:
            already.append((-graph[i][j] , i+1, j+1))
        else:
            edge.append((graph[i][j] , i+1 , j+1))

edge.sort(key=lambda x:x[0])

for value,x,y in already:

    x=Find(x)
    y=Find(y)
    total += value

    if x!=y:
        if x>y:
            disjoint[x]=y
        else:
            disjoint[y]=x

total//=2
for value,A,B in edge:

    x=Find(A)
    y=Find(B)

    if x!=y:
        if x>y:
            disjoint[x]=y
        else:
            disjoint[y]=x
        check.append([A,B])
        total+=value

print(total , len(check))

for i in check:
    print(*i)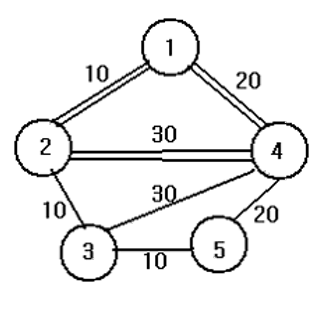

📌 어떻게 접근할 것인가?

최소 스패닝 트리 문제 입니다. 크루스칼 알고리즘을 통해 구현했습니다.

이미 설치된 도시에 대해서는 전부다 연결을 해주고

그다음에 나머지 간선들을 정렬해서 연결해줍니다.

이때 연결된 노드를 저장하고 마지막에 출력해줘야 합니다.