백준 21738 : 얼음깨기 펭귄 (Python)

본문 링크

"""
펭귄에 있는 위치는 항상 기본 얼음이기 때문에 2개이상의 지지대가 필요하다.
이떄 최대한 많은 얼음을 깰려면 지지대로부터 가장 짧은 최단 경로를 구하고
전체 블록 개수 - 지지대로부터 가장 짧은 최단경로 2개 - 펭귄이 서있는 블록 1개 이다.
최단경로는 그냥 DFS 를 돌려서 2개 찾자.

서로 다른 두 얼음을 잇는 경로는 하나뿐이다 , 즉 O(N) 으로 가능
S는 무조건 2 이상.
"""

def DFS(Node,level):

    visit[Node]=True
    if Node==P:
        visit[P]=False
        if len(length)<=1:
            length.append(level)
        else:
            if level < max(length):
                del length[length.index(max(length))]
                length.append(level)
        return
    for i in Tree[Node]:
        if not visit[i]:
            DFS(i,level+1)
import sys
input=sys.stdin.readline
sys.setrecursionlimit(10**9)

N,S,P=map(int,input().split())
Tree=[ [] for _ in range(N+1) ]

for i in range(N-1):
    A,B=map(int,input().split())
    Tree[A].append(B)
    Tree[B].append(A)

visit=[False]*(N+1)
length=[] # 길이 저장 배열

for i in range(1,S+1): # 지지대에서 출발
    if not visit[i] and i!=P:
        DFS(i,0)

print(N-sum(length)-1)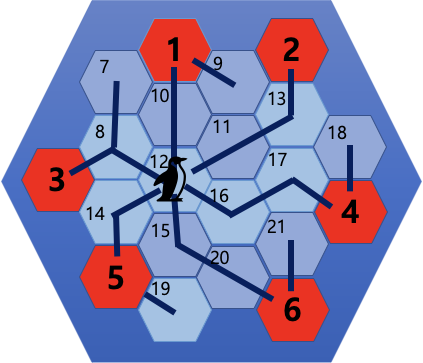

📌 어떻게 접근할 것인가?

이문제는 문제를 꼼꼼하게 읽어봐야한다.

문제에서는 총 2가지의 블록이 있다.

• 지지대 블록
• 일반 블록

지지대 블록은 트리 형식으로 다른 블록과 연결되어있다. 이때 문제에서 서로 다른 두 얼음을 연결하는 경로는 단 하나뿐이기 때문에 사이클이 없다. 즉 트리 그래프이다.

그리고 다음으로 얼음이 깨지는 조건이다.

일반 얼음의 경우에는 1개의 지지대만이 연결되어 있어도 얼음이 깨지지 않지만 펭귄이 올라가 있는 얼음은 2개 이상의 지지대의 역할을 하는 얼음이 연결되어 있어야만 얼음이 깨지지 않는다

다만 문제에서 "게임 시작 시 펭귄은 일반 얼음 위에 위치해 있고 어떤 얼음도 깨지지 않은 상태로 시작하게 된다. " 라고 하였기 때문에 펭귄이 떨어질 조건은 하나가 된다.

• 일반 얼음위에있는 펭귄이 지지대가 연결되어있는 경로가 2개 미만일 때

그리고 우리는 얼음을 깰수있는 최대값을 구하고자 한다.

그러면 펭귄이 살아남기 위해서는 반대로 생각하면

지지대에서 펭귄으로 가는 최단 경로 2개를 제외한 나머지 얼음을 전부 부순다. 라는 조건이 성립한다.

따라서 $DFS$ 탐색을 통해 최단경로 2개를 찾은 뒤에

$print(N-sum(length)-1)$ 을 출력한다.