최장 증가 부분 수열 - LIS

📌LIS 알고리즘 이란?

최장 증가 부분 수열 - (LIS : Longest Increasing Subsequence)

동적 계획법 알고리즘을 응용한 알고리즘 입니다.

❓ 어떤 임의의 수열이 주어졌을때 가장 긴 증가하는 부분수열의 길이는 얼마인가?

를 구하는 알고리즘입니다.

예를들어 다음과 같은 수열이 있다고 가정할때

3 5 7 9 2 1 4 8

증가하는 부분수열은 아주 많습니다.
3 5 | 3 5 7 9 | 3 5 8 | 5 7 8 | 3 8 ~

또한 부분수열은 꼭 연속일 필요는 없습니다.

이때 가장 긴 증가하는 부분 수열은 3 5 7 9 or 3 5 7 8 입니다.
따라서 $LIS$ 는 4가 됩니다.
하나의 수열에서 $LIS$ 는 여러개가 나올수 있습니다.

🔑 $O(N^2)$ 풀이법

가장 긴 증가하는 부분 수열 1

N=int(input())

L=list(map(int,input().split()))

dp=[0]*N

for i in range(N):
    for j in range(i):
        if L[i]>L[j] and dp[i] < dp[j]:
            dp[i]=dp[j]
    dp[i]+=1
print(max(dp))

이중 반복문을 사용하여서 모든 리스트 값을 탐색하는 방법입니다.
이때 L[i] > L[j] and dp[i] < dp[j] 를 통해 수열이 증가하면서 이전에 증가했던 횟수보다 큰지 확인합니다.

예제 입출력을 보았을때

• 입력
  6
  10 20 10 30 20 50
• 출력
  4

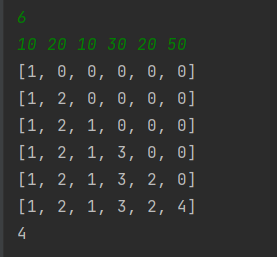
10 , 20 처럼 증가할때는 $dp$ 값을 1 증가시키고
다시 10으로 감소했다면 10이하의 값중 $dp$ 최대값을 가져옵니다.
다시 30으로 증가했다면 30이하의 $dp$ 최대값+1을 가져옵니다.

가장 긴 감소하는 부분은 if 문 코드를 아래와 같이 수정하면됩니다

if L[i]>L[j] and dp[i] < dp[j] - 가장 긴 증가하는 부분수열

if L[i]<L[j] and dp[i]<dp[j] - 가장 긴 감소하는 부분수열

🔑 $O(N^2)$ - 역추적

이번에는 $dp$ 테이블을 이용하여서 가장긴 증가하는 부분수열의 배열을 구할수 있습니다.

check=[]
K=max(dp)+1
for i in range(-1,-N-1,-1):
    if K-1==dp[i]:
        K=dp[i]
        check.append(L[i])
check.reverse()
print(*check)

기존 $O(N^2)$ 풀이법에서 check 빈 배열을 만들어줍니다.
이후 K=max(dp)+1 로 잡아주고 $dp$ 배열의 뒤에서 부터 처음으로 감소하는 지점을 확인해줍니다.

이 사진을 다시보면 처음으로 감소하는 지점을 보겠습니다.

• 배열의 인덱스가 5 일때 - 4
• 배열의 인덱스가 3 일때 - 3
• 배열의 인덱스가 1 일때 - 2
• 배열의 인덱스가 0 일떄 - 1

이렇게 처음으로 감소하는 지점을 체크해주면
인덱스가 5 , 3, 1 , 0 이고 이를 뒤집으면 0 , 1 , 3 , 5 가 됩니다.
따라서 dp[0]=10 , dp[1]=20 , dp[3]=30 , dp[5]=50 으로
가장 긴 증가하는 배열을 구할수 있습니다.

🔑 $O(Nlog N)$ 풀이법 - 이분탐색

이번에는 $LIS$ 를 $O(Nlog N)$ 으로 해결하는 방법에 대해 알아보겠습니다.

바로 이분탐색을 이용하여 $dp$ 배열에 $LIS$ 를 유지하기 위한 최적의 위치에다가 수를 삽입하는 방식입니다.

자리를 찾는데 lower_bound 를 이용하기 때문에 $O(logN)$ 의 시간복잡도를 가지게 되어 총 $O(NlogN)$ 의 시간복잡도를 가지게 됩니다.

일단 입력받을 리스트와 $DP$ 테이블을 만들어 보겠습니다.

$L=[10,20,40,25,20,50,30,70,85]$

$dp=[10]$

현재 $dp$ 테이블에는 10 이 저장되어있습니다.
그리고 이제 값이 증가해주면 증가값을 그대로 $dp$ 에 저정해줍니다.

$dp=[10,20,40]$

하지만 이때 25 로 값이 감소했을때 25 를 dp 배열중 넣을수있는 최적에 장소에 값을 삽입입합니다.

따라서 다음 $dp$ 값은 $dp=[10,20,25]$ 가 됩니다.

이때 우리는 dp 를 항상 오름차순으로 정렬했기때문에 이분탐색이 가능합니다.

즉 특정 값이 감소할때 그 값을 dp 배열에 넣을때 최적의 장소를 이분탐색으로 값을 삽입합니다.

따라서 $dp$ 배열의 변화는 아래와 같습니다.

• $dp=[10,20,25,50]$
• $dp=[10,20,25,30]$
• $dp=[10,20,25,30,70]$
• $dp=[10,20,25,30,70,85]$

따라서 우리는 $LIS$ 값이 6 이 됨을 확인할수 있습니다.

이분탐색 코드는 아래와 같습니다.

N=int(input())
L=list(map(int,input().split()))

dp=[0]

for i in L:
    if dp[-1]<i:
        dp.append(i)
    else:
        start=0 ; end=len(dp)-1 # 이분탐색을 L 리스트가 아니라 이미 정렬된 DP 리스트에서 탐색한다.
        while start<=end:
            mid=(start+end)//2
            if dp[mid]<i:
                start=mid+1
            else:
                end=mid-1
        if start>=len(dp): #start값이 dp의 길이보다 크거나 같으면 그냥 붙인다.
            dp.append(i)
        else:
            dp[start]=i
print(len(dp)-1)

🔑 $O(Nlog N)$ 풀이법 - bisect

파이썬에는 특정 배열과 값이 있으면 그 값을 최적의 인덱스를 반환해주는 함수가 있습니다.

바로 bisect 라이브러리 입니다.

이때 bisect_left 를 import 하고 사용했을때
bisect_left(#배열,#값) 이 가지는 의미는
배열에서 특정한 값보다 크거나 같은 최소 인덱스는 얼마인가? 를 찾아줍니다.

예를들면 $dp=[1,2,3,5]$ 가 있다고 하면
이때 bisect_left(dp,4) 은 5 가 들어있는 인덱스 값인 3 을 반환해줍니다.

즉 이분탐색 코드를 구현하지 않아도 알아서 최적의 장소를 찾아주기때문에 아주 유용한 라이브러리입니다.

또한 bisect 는 실제 이분탐색을 구현한 코드보다 속도가 더 빠르니 가능하면 bisect 라이브러리를 사용하는것이 좋습니다.

아래는 bisect 를 활용한 코드입니다.

from bisect import bisect_left

N=int(input())
L=list(map(int,input().split()))

dp=[ L[0] ]
answer=1

for i in L:
    if dp[-1]<i:
        dp.append(i)
        answer+=1
    else:
        index=bisect_left(dp,i)
        dp[index]=i

print(answer)

🔑 $O(Nlog N)$ - 역추적

$O(Nlog N)$ 으로 $LIS$ 길이를 구할때 $dp$ 배열은 실제 가장 긴 증가하는 배열이 아닙니다. 매번 특정 값을 $dp$ 배열에 최적의 장소에 넣었을뿐 , 실제로 가장 긴 증가하는 배열을 의미하지 않습니다.

따라서 가장 긴 증가하는 부분수열을 구하기 위해서는 인덱스 값을 역추적 해야합니다.

N=int(input())
L=list(map(int,input().split()))
dp=[]
check=[]

for i in L:
    if not dp:
        dp.append(i)
    if dp[-1]<i:
        dp.append(i)
        check.append((len(dp) - 1, i)) #check
    else:
        index=bisect_left(dp,i)
        check.append( (index,i)) #check
        dp[index]=i

answer=[]
last_index=len(dp)-1
for i in range(len(check)-1,-1,-1):
    if check[i][0]==last_index:
        answer.append(check[i][1])
        last_index-=1
print(len(answer))
print(*answer[::-1])

check 배열을 따로 만들어 주어서 $dp$ 배열에 값이 추가될때마다
$dp$ 의 길이와 그때의 값을 저장해줍니다.

그리고 이전의 $O(N^2)$ 의 역추적과 비슷한 방법으로
가장 처음으로 감소하는 지점을 매번 찾아서 answer 배열에 그때의 값을 저장해줍니다.

따라서 $O(Nlog N)$ 풀이와 함께 $LIS$ 의 값과 가장 긴 증가하는 실제 배열을 구할수 있습니다.

📌가장 긴 바이토닉 부분수열

가장 긴 바이토닉 부분수열

마지막으로 알아볼 내용은 $LIS$ 알고리즘을 살짝 변형시킨 바이토닉 부분수열입니다.
수열 $S$가 어떤 수 $S_k$를 기준으로
$S_1 < S_2 < ... S_k-1 < S_k > S_k+1 > ... S_N-1 > S_N$을 만족한다면, 그 수열을 바이토닉 수열이라고 합니다.

1 5 2 1 4 3 4 5 2 1 라는 배열이 있을때
가장 긴 바이토닉 부분수열은 1 2 3 4 5 2 1 입니다.
즉 한번 쭉 증가하면서 한번 쭉 감소하는 가장 긴 수열을 찾으면됩니다.

N=int(input())

a=list(map(int,input().split()))
Reverse=a[::-1]
dp1=[0]*N
dp2=[0]*N

answer=0
for i in range(N):
    for j in range(i):
        if a[i]>a[j] and dp1[i]<dp1[j]:
            dp1[i]=dp1[j]
        if Reverse[i]>Reverse[j] and dp2[i]<dp2[j]:
            dp2[i]=dp2[j]
    dp1[i]+=1
    dp2[i]+=1

dp2.reverse()
for i in range(N):
    answer=max(answer,dp1[i]+dp2[i])
print(answer-1)

바이토닉 부분수열은 입력받은 리스트와 그 리스트를 거꾸로한 리스트 2개를 비교해줍니다.
따라서 $dp$ 배열이 총 2개가 필요하며 기존리스트에서 가장 긴 증가하는 부분수열 , 역순 리스트에서 가장 긴 증가하는 부분수열 2개를 구해줍니다.

이때 역순으로 가장 긴 증가하는 부분수열을 구했기 때문에 $dp2$ 는 reverse 해줍니다.

이후 answer=max(answer , dp1[i]+dp2[i]) 값을 저장해줍니다.
dp1[i]+dp2[i]는 {1 5 2 1 4 3 4 5 2 1} 배열에서
증가하는 부분 - 1 3 4 5 | 감소하는부분 - 2 1 의 길이를 더한 값이 됩니다.

📌 Conclusion

지금까지 $LIS$ 알고리즘이 무엇인지 , 그것을 풀기위한 $O(N^2)$ 과 $O(Nlog N)$ 풀이방법 , $LIS$ 실제 배열을 구하는 방법 , 마지막으로 바이토닉 부분 수열에 대해 알아보았습니다.

LIS 문제집 LIS는 백준에 시리즈별로 다양하게 있으니 이 문제집을 통해 공부하시는걸 추천합니다.

다음에는 $LCS$ (최장 공통 부분수열) 알고리즘에 대해 알아보겠습니다.