그래프(Graph)에 대하여
1) 그래프와 관련된 수학적 규칙에 대하여
- 그래프의 노드(정점이라고도 함)와 노드를 이은 선을 간선(edge)이라고 하고, 한 노드를 기준으로 다른 노드와 이어진 간선의 수를 '차수'라고 한다. 이 때, 전체 차수의 합은 간선의 2배가 된다. 이유는 차수를 더하다보면 결국 각 노드의 차수를 한번씩더 더해주게 되기에 간선에 두배를 한 값이 차수의 합이 된다.
- 전체 간선의 수는 정점의 수의 제곱보다 작거나 같다.
- 용어적인 측면에서 싸이클이라는 용어도 있는데, 특정 정점에서 출발하여 다시 그 특정 정점으로 돌아오는 경로를 말한다.
2) 그래프의 특징
: 지하철 노선도, 페이스북의 인간관계 네트워크 등 다양한 일상 속의 현상을 그래프로 표현할 수 있어서, 실용적으로 자주 쓰이고, 그에 따른 이론들도 많음.
3) 그래프의 구현 방법 : 인접 행렬 vs 인접 리스트
- 인접 행렬 방법 :
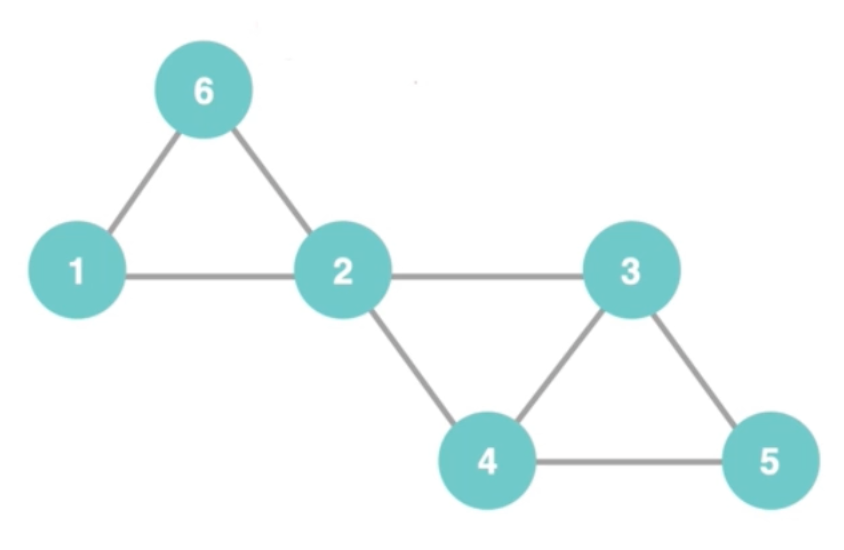
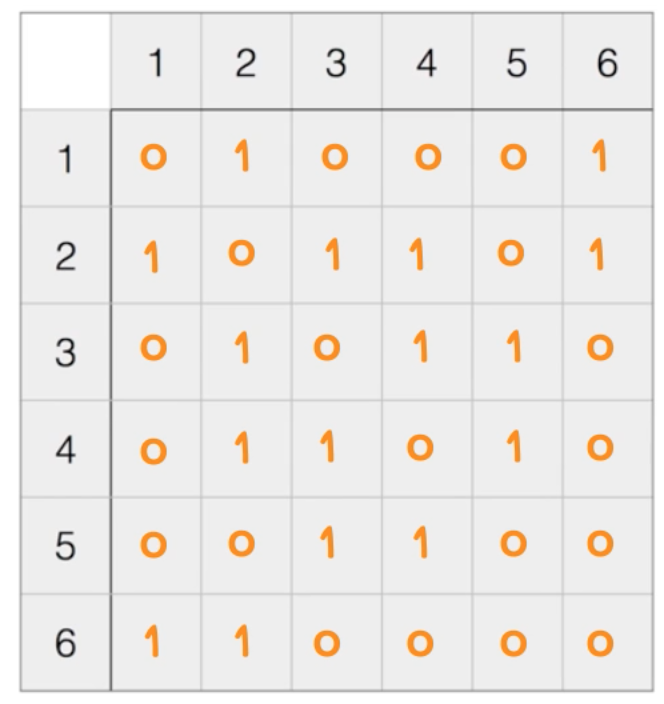
: 위의 두개의 그림으로 설명해보면, 먼저, 맨 위의 그림이 그래프를 표현한 그림이다. 그리고 각각의 번호가 담긴 파란색 원이 정점(Node)가 되고, 그 노드들을 서로 이은 것이 차선(edge)가 된다. 그러면 밑에 표는 무엇인가하면, 각각의 노드들이 연결되어있는지에 대한 정보를 담은 표이다. row1을 보면 행은 1이고 열에 1,2,3,4,5,6이 순서대로 표시돼있고, 거기에 0,1의 값이 채워져있는데, 이는 1이라는 노드와 1,2,3,4,5,6이라는 노드들이 각각 연결되어있는지의 여부를 표현하는 것이다. 1로 돼있으면 연결돼있다는 표시이고, 0으로 돼있으면 연결되지 않았다는 표시이다.
: 실제로 위의 인접 행렬을 코드로 구현해보면,
: 이렇게 위에 l에서 인접한 노드 정보를 담고, 그 정보를 바탕으로 접점의 개수를 N이라 할 때 NXN 행렬(배열)을 만든 다음에, 인접 노드 정보를 바탕으로 연결돼있으면 1을 채워놓으면 된다.
: 위의 인접 행렬을 출력해보면 다음과 같다.
-
그렇다면 위와 같은 인접행렬로 그래프를 구현하면 장점과 단점이 어떻게 될까?
1) 특정 노드 x와 y가 인접해있는지를 알기 위해 O(1)의 시행만 하면된다. 저 배열로 치면 graph[1][4]만 해주면 노드 2와 5가 인접해있는지를 알 수 있다는 것이다(장점).
2) 만약 특정 노드 x와 연결된 노드를 모두 알고 싶을 때는 실제로 연결된 노드의 개수와 상관없이 접점의 개수만큼의 시행을 해야한다(O(N))[단점].
3) 또한, 인접 행렬을 구현하려면, 차선의 개수에 상관없이 무조건 노드의 개수 * 노드의 개수 만큼의 배열로 구현해야한다(단점). -
인접 리스트 방법 :
: 위와 똑같은 그래프를 이번에는 인접 리스트로 구현해보면,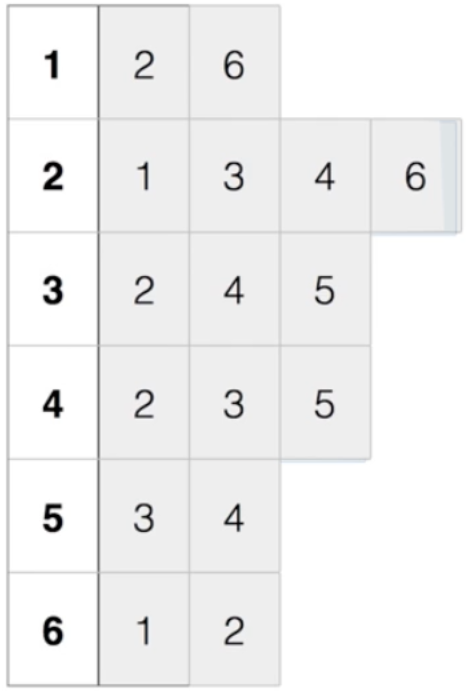
: 위와 같이 구현해볼 수 있다. -
인접 리스트의 장점과 단점
1) 특정 노드 x,y가 인접해있는지 알려면 둘중하나의 노드에 연결된 모든 노드를 체크해야(최악의 경우) 알 수 있다(단점).
2) 특정 노드에 인접한 모든 노드를 알기 위해서는 굳이 인접하지 않은 노드까지 찾아볼 필요없이 한번에 알 수 있다(장점).
3) 연결된 노드 이외의 정보를 담지 않아도 된다. 즉, 서로 연결되어 있지 않은 노드의 정보까지 담지 않아도 된다(장점). -
결과적으로 인접행렬과 인접리스트는 보완관계인 것을 알 수 있는데, 인접 행렬의 단점이 인접 리스트에서 해결되어 장점이되고, 인접 리스트의 단점이 인접 행렬에서 해결돼 장점이 되는 것을 볼 수 있다.
-
인접 리스트도 실제로 구현해보면, 다음과 같다.
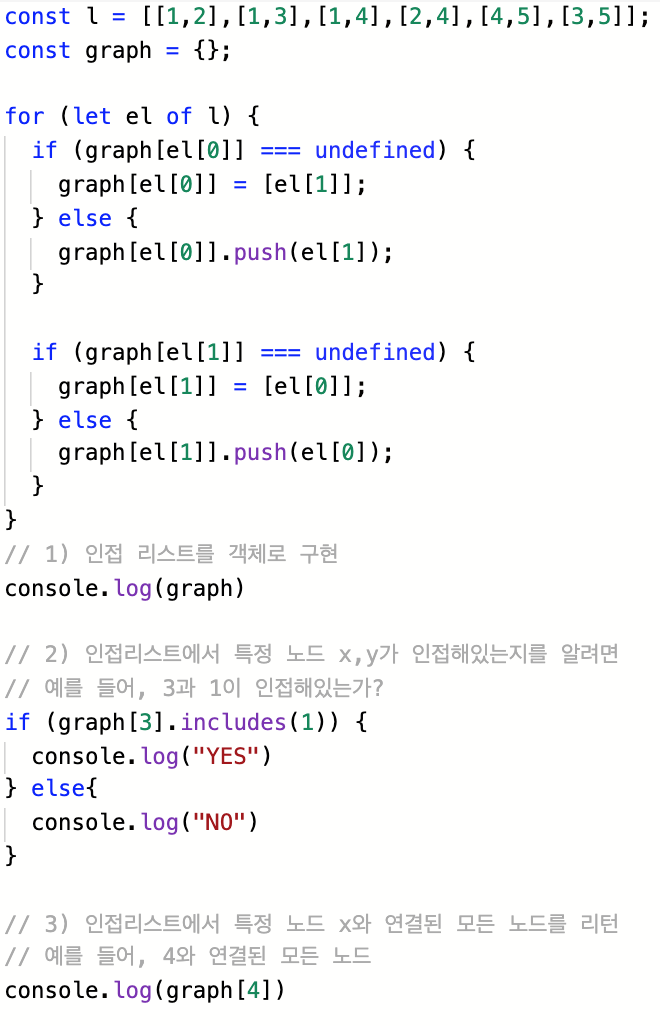
그리고 아래는 각각의 물음에 대한 출력이다.
