


: 알고리즘 잡스에서 푼 문제중에 역대급.. 이거 결국 혼자 힘으로는 60점 밖에 못냈고 3일에 걸쳐서 풀었다.. 이렇게 풀면 안되긴 하는데 이 고비를 스스로 넘겨야 할 것 같았다..BFS ^^
문제 해석
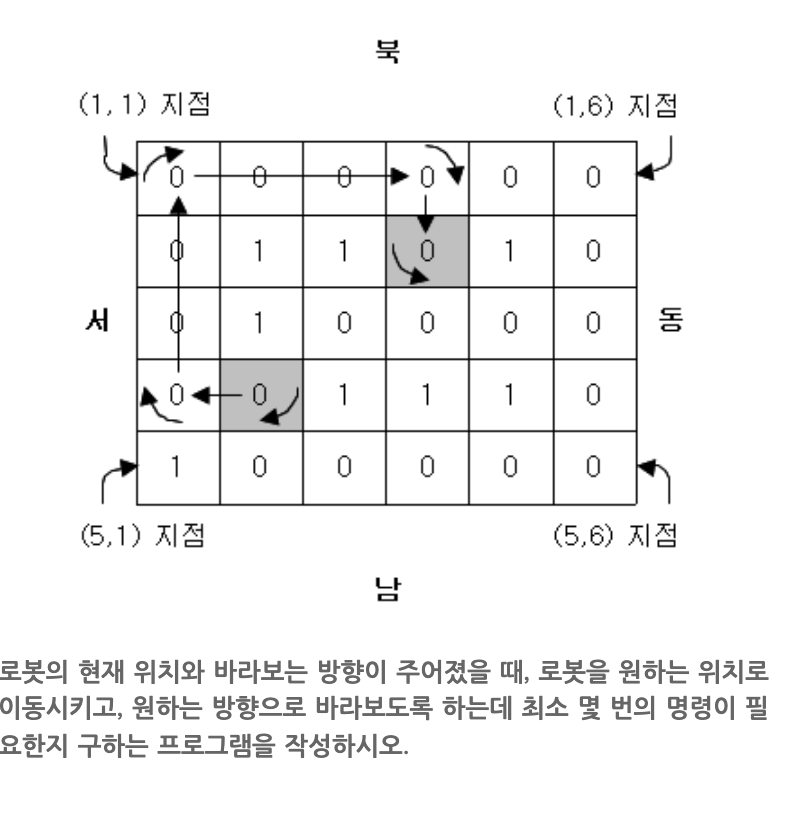
: 특정 좌표에서 로봇에게 명령을 내려(1,2번) 특정 좌표로 이동하게 할 때 최소 몇번의 명령을 내려서 갈 수 있는지를 구하는 문제이다. 이 때, 명령1은 k만큼 앞으로 전진하도록 하는 것인데, 주어진 궤도에서만 전진이 가능하다. 즉, 0인 칸에서만 전진이 가능하고, 1로는 갈 수 없다. 그리고 k는 1에서 3 사이로 최대 3칸까지 전진이 가능하다(한번의 명령으로). 명령2는 방향을 바꾸는 명령인데 현재 방향을 기준으로 오른쪽, 왼쪽으로만 방향을 바꿀 수 있다. 예를 들어, 동쪽을 바라보고 있는 상태라면 북쪽과 남쪽으로만 방향을 바꿀 수 있다. 입력은 로봇이 움직일 궤도 정보와 그 궤도 정보가 NxM 행렬일 때, N,M의 정보, 그리고 로봇의 시작 좌표 및 시작 방향과 도착 좌표 및 도착 방향을 준다. 이를 바탕으로 최소 명령수를 리턴하면 되는 문제이다.
내가 헤맸던 포인트
: 사실 헤맸던 포인트라는 워딩(?)이 무색할 정도로 이 문제를 어떻게 접근할지 갈피조차 잡지 못했다. 처음에 평소 하던대로 탐색 공간을 알아봤고, 최소 거리를 구하는 문제이기에 BFS를 떠올렸다. 하지만, 내가 여태까지 풀었던 BFS 문제들은 대부분이 탐색하면서 하나의 값만 저장하면서 탐색을 했었는데, 이번에는 그 조건들이 다양했던 문제여서 머리가 복잡했고, 해결책을 찾기가 쉽지 않았다. 후회되는 포인트는 차라리 빨리 질문을 계속해서 문제를 푸는게 나았던 것 같다. 같은 문제를 계속해서 보니까 계속 같은 생각만하고 무한루프가 돌더라..
어쨌든 헤맸던 포인트를 정리해보면,
- 문제를 제대로 읽지 않았다. 문제에서 주어진 명령어 1에서 k가 1 or 2 or 3인 것을 읽었음에도 왜 그랬는지 모르겠지만 그냥 한 방향으로 처음부터 끝까지 자유자재로 갈 수 있다고 생각하고 풀었다. 이에 더하여.. 명령어 2도 동서남북을 자유자재로 전환할 수 있다는 의미로 해석했다. 즉, 북쪽을 향하고 있을 때는 동쪽, 서쪽으로만 전환을 할 수 있는건데, 남쪽에서 북쪽으로도 전환이 되는줄 알았다.
- BFS를 떠올리긴 했지만, 탐색을 하면서 어떤 값을 기준으로 탐색을 할지 갈피를 못잡았다. 이 문제에서는 결국 '명령어'를 기준으로 해당 명령어를 실행했을 때 위치하게 되는 좌표 및 방향을 큐에 쌓으면서 탐색을 해야하는 문제였다. 해당 좌표 및 방향이 pop되면 그 좌표 및 방향에서 갈 수 있는 또다른 가지수를 queue에 넣는식으로 진행되는 것이다. 하지만, 명령을 통해 나온 좌표 및 방향 값을 큐에 넣으면서 해당 정보에서 또다른 자식 정보를 pop하는 식의 BFS가 나에게 너무 낯설었던 것 같다. 이 발상과 이 발상을 구현하는데에 시간을 오래 썼다.
- 간단한 for문을 통해 구현할 수 있는 것을 코드가 너무 길어지게 짜서 디버깅이 힘들게 코드를 짰다. 그에 따라 실제로 오타 하나 때문에 30분 이상을 지체했다..
다음으로 고칠점을 정리해보면
- 단순 반복되는 부분은 여러줄의 if문 보다는 자료구조를 잘 이용해서 간소화시키자. 코드가 길어질수록 에러를 만들어낼 확률이 너무나도 높아진다. 또한, 에러가 없더라도 마지막에 문제를 못풀었을 경우 다시 돌아가서 코드를 봐야하기 때문에 그런 상황을 대비해서라도 코드를 간소화하는 노력을 하자
- 한시간 이상 문제가 안풀리거나 갈피를 못잡으면 질문을 하고 힌트를 얻자. 그리고 한문제에 하루를 넘기지말자
- 잔실수가 많은데 이는 위의 코드 간소화로 해결해보려고 노력하자.
- 네이버, 라인 등의 코딩테스트 대비를 위해 테스트 케이스를 내가 직접 만들어서 해보는 연습을 하자.
문제 설계
: 이 문제를 해결하기 위한 포인트는 하나의 위치 및 바라보는 방향을 한개의 정보 단위로 정하고, 그 정보 단위를 하나의 노드로 생각하고, 이를 그래프화해서 BFS를 한다는 생각을 하는 것이다. 나에게는 여전히 복잡한 얘기인데, 천천히 따라가보면, 먼저, BFS라는 것 자체가 그래프라는 자료구조를 바탕으로 이뤄지는 알고리즘이다. 루트 노드를 기준으로 각 높이마다 자식 노드를 한층씩 쭉 훑으면서 가장 아래쪽 층까지를 순차적으로 탐색하는 방식이라고 할 수 있다. 이 때, 루트 노드를 이 문제에서 '방향 정보 + 좌표 정보'라고 했을 때 루트 노드에서 만들 수 있는 혹은 나아갈 수 있는 새로운 정보들을 나열해보면, 예를 들어, 루트 노드가 (5,4,남쪽 방향)이라는 정보라면, 이 정보를 바탕으로 만들 수 있는 혹은 나아갈 수 있는 자식 노드들은 이렇게 된다.
- 명령어 2를 통해 이뤄진 방향 전환이 이뤄진 정보
1) (5,4, 동쪽)
2) (5,4, 서쪽) - 명령어 1을 통해 이뤄진 전진한 좌표 정보(현재 남쪽을 보고 있으므로 x축으로 +1씩 전진함)
1) (6,4, 남쪽)
2) (7,4, 남쪽)
3) (8,4, 남쪽)
이런식으로 총 5개의 명령어를 새로 입력하여 새로운 좌표값과 방향을 얻을 수 있다. 그리고 이는 모든 노드에서 동일하게 5개의 명령어를 입력할 수 있다. 모든 노드에서 오른쪽, 왼쪽으로 방향 전환을 할 수 있을 것이고(2개), 향하던 방향으로 1,2,3칸씩 움직이도록 명령할 수 있다(3개).
여기서 다시 우리가 최종적으로 구하고자 하는 값을 상기시켜보면 특정 좌표로 가기 위한 최소 명령어의 수였다. 그러면 BFS를 하면서 특정 좌표에 도착할 때까지 쓰인(?) 명령어의 개수를 표기하면서 진행해야하고, 마지막에 도착하고자 하는 좌표에 그 때까지 쓰인 최소 명령어가 적히도록 해야한다. 하지만 이번 문제는 그리 간단하지 않다.. 생각해야할 정보가 한개가 아닌 두개 이상이다. 그래서 여기서는 아예 방향 별로 배열을 따로 만든다음에 풀어줘야한다. 동쪽을 향하는 케이스에서 생기는 정보들은 동쪽용(?) 배열에 입력하고, 서쪽을 향하는 케이스에서의 정보들은 서쪽용 배열에 입력하는 것이다. 이렇게 해야지만, 최종 목적지에 도달한 최소 명령어 수를 구할 수 있는데, 이유는 이렇게 안하면 예를 들어, 도착지를 갈 수 있는 방법이 동쪽을 향해 가다가도 갈 수 있고, 서쪽을 향해 가다가도 갈 수 있는 곳이라면, 둘중에 어떤 곳이 여태까지 명령어를 더욱 조금 입력해왔는지 알 수가 없다. 분명 이전의 방식대로라면 겹치는 부분을 탐색하지 않을 것이기에 방향별로 나눠서 생각해야한다.
import copy
n, m = map(int, input().split())
board = []
for i in range(n):
board.append([1,1,1]+list(map(int, input().split()))+[1,1,1])
limit_line = [[1 for i in range(m+6)],[1 for i in range(m+6)],[1 for i in range(m+6)]]
board = limit_line + board + limit_line
a,b,w1 = map(int, input().split())
c,d,w2 = map(int, input().split())
ways = {}
for i in range(1,5):
copy_board = []
for j in range(n+6):
row = []
for k in range(m+6):
if board[j][k] == 0:
row.append(None)
elif board[j][k] == 1:
row.append("NULL")
copy_board.append(row)
ways[i] = copy_board
queue = [(w1,a+2,b+2)]
ways[w1][a+2][b+2] = 0
dx = [None, 0, 0, 1, -1]
dy = [None, 1, -1, 0, 0]
possible_dir = [None,[3,4],[3,4],[1,2],[1,2]]
while len(queue) != 0:
top = queue.pop(0)
for i in possible_dir[top[0]]:
if ways[i][top[1]][top[2]] is None:
ways[i][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
queue.append((i,top[1],top[2]))
# if top[0] == 1:
# if ways[3][top[1]][top[2]] is None:
# ways[3][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((3,top[1],top[2]))
# if ways[4][top[1]][top[2]] is None:
# ways[4][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((4,top[1],top[2]))
# elif top[0] == 2:
# if ways[3][top[1]][top[2]] is None:
# ways[3][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((3,top[1],top[2]))
# if ways[4][top[1]][top[2]] is None:
# ways[4][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((4,top[1],top[2]))
# elif top[0] == 3:
# if ways[1][top[1]][top[2]] is None:
# ways[1][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((1,top[1],top[2]))
# if ways[2][top[1]][top[2]] is None:
# ways[2][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((2,top[1],top[2]))
# elif top[0] == 4:
# if ways[2][top[1]][top[2]] is None:
# ways[2][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((2,top[1],top[2]))
# if ways[1][top[1]][top[2]] is None:
# ways[1][top[1]][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((1,top[1],top[2]))
# 여기까지 방향끝
# 여기서부터 직진 1<=k<=3
for step in range(1,4):
if ways[top[0]][top[1]+(dx[top[0]]*step)][top[2]+(dy[top[0]]*step)] is None:
ways[top[0]][top[1]+(dx[top[0]]*step)][top[2]+(dy[top[0]]*step)] = ways[top[0]][top[1]][top[2]] + 1
queue.append((top[0],top[1]+(dx[top[0]]*step),top[2]+(dy[top[0]]*step)))
else:
break
# if top[0] == 1:
# prev = False
# if ways[top[0]][top[1]][top[2]+1] is None:
# prev = True
# ways[top[0]][top[1]][top[2]+1] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]+1))
# if ways[top[0]][top[1]][top[2]+2] is None and prev:
# prev = True
# ways[top[0]][top[1]][top[2]+2] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]+2))
# if ways[top[0]][top[1]][top[2]+3] is None and prev:
# ways[top[0]][top[1]][top[2]+3] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]+3))
# elif top[0] == 2:
# prev = False
# if ways[top[0]][top[1]][top[2]-1] is None:
# prev = True
# ways[top[0]][top[1]][top[2]-1] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]-1))
# if ways[top[0]][top[1]][top[2]-2] is None and prev:
# prev = True
# ways[top[0]][top[1]][top[2]-2] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]-2))
# if ways[top[0]][top[1]][top[2]-3] is None and prev:
# ways[top[0]][top[1]][top[2]-3] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1],top[2]-3))
# elif top[0] == 3:
# prev = False
# if ways[top[0]][top[1]+1][top[2]] is None:
# prev = True
# ways[top[0]][top[1]+1][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]+1,top[2]))
# if ways[top[0]][top[1]+2][top[2]] is None and prev:
# prev = True
# ways[top[0]][top[1]+2][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]+2,top[2]))
# if ways[top[0]][top[1]+3][top[2]] is None and prev:
# ways[top[0]][top[1]+3][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]+3,top[2]))
# elif top[0] == 4:
# prev = False
# if ways[top[0]][top[1]-1][top[2]] is None:
# prev = True
# ways[top[0]][top[1]-1][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]-1,top[2]))
# if ways[top[0]][top[1]-2][top[2]] is None and prev:
# prev = True
# ways[top[0]][top[1]-2][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]-2,top[2]))
# if ways[top[0]][top[1]-3][top[2]] is None and prev:
# ways[top[0]][top[1]-3][top[2]] = ways[top[0]][top[1]][top[2]] + 1
# queue.append((top[0],top[1]-3,top[2]))
if isinstance(ways[w2][c+2][d+2],int):
print(ways[w2][c+2][d+2])
break
: 위에는 풀이 코드인데, 중간에 주석 처리한 것은 처음에 너무 하드코딩으로 만들어서 간소화 시킨 부분을 주석처리 해놓은 것이다.
마무리
: 이 문제는 두고두고 풀어봐야겠다..
21/09/30 다시 풀어보기
import copy
n,m = map(int, input().split())
board = []
for i in range(3):
board.append(["BLOCK" for k in range(m+6)])
for i in range(n):
input_list = list(map(int, input().split()))
for j in range(m):
for idx,el in enumerate(input_list):
if el == 0:
input_list[idx] = "ROAD"
elif el == 1:
input_list[idx] = "BLOCK"
board.append((["BLOCK"]*3) + input_list + (["BLOCK"]*3))
for i in range(3):
board.append(["BLOCK" for k in range(m+6)])
maps = {}
for way in range(1,5):
copy_board = copy.deepcopy(board)
maps[way] = copy_board
a,b,w1 = map(int,input().split())
c,d,w2 = map(int,input().split())
root = (w1,a+2,b+2)
queue = [root]
maps[root[0]][root[1]][root[2]] = 0
def check_direction(top):
global maps
global queue
possible_dir = [None, [3,4],[3,4],[1,2],[1,2]]
for d in possible_dir[top[0]]:
if maps[d][top[1]][top[2]] == "ROAD":
maps[d][top[1]][top[2]] = maps[top[0]][top[1]][top[2]] + 1
queue.append((d,top[1],top[2]))
def check_forward(top):
global maps
global queue
direction = top[0]
dx = [None, 0, 0, 1, -1]
dy = [None, 1, -1, 0, 0]
for i in range(1,4):
if maps[direction][top[1]+(dx[direction]*i)][top[2]+(dy[direction]*i)] == "ROAD":
maps[direction][top[1]+(dx[direction]*i)][top[2]+(dy[direction]*i)] = maps[direction][top[1]][top[2]] + 1
queue.append((direction, top[1]+(dx[direction]*i), top[2]+(dy[direction]*i)))
else:
break
while len(queue) != 0:
top = queue.pop(0)
check_direction(top)
check_forward(top)
if isinstance(maps[w2][c+2][d+2], int):
print(maps[w2][c+2][d+2])
break
: 함수를 만들어서 메인 로직의 코드를 간소화 시켰다. 이런식으로 해야 에러를 만드는 수가 줄어들 것 같다.
