[Algorithm] 로봇 청소기 문제

문제

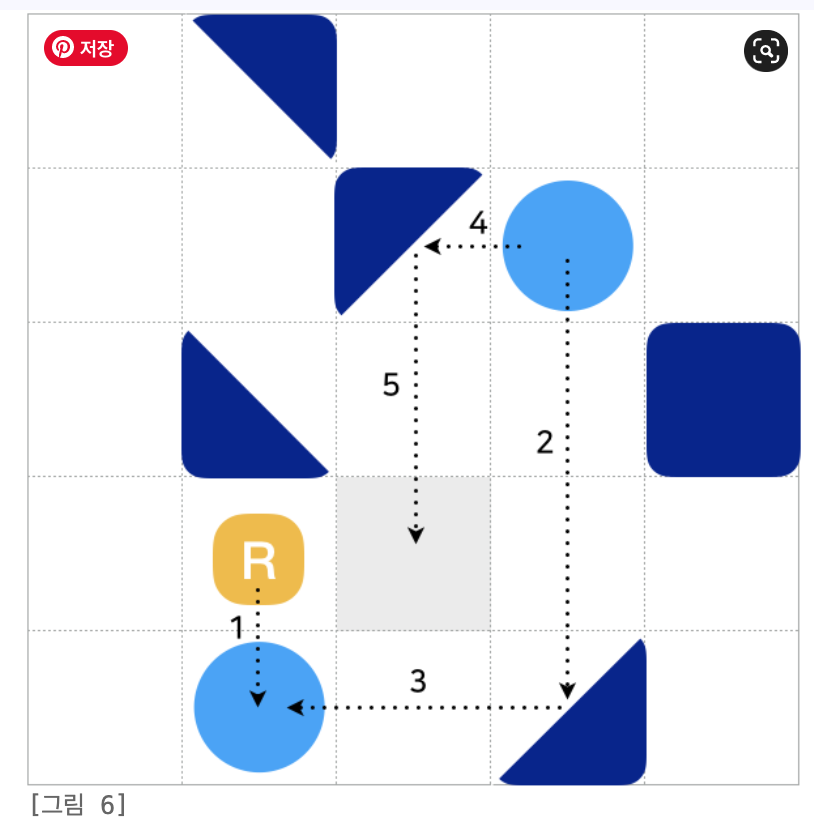
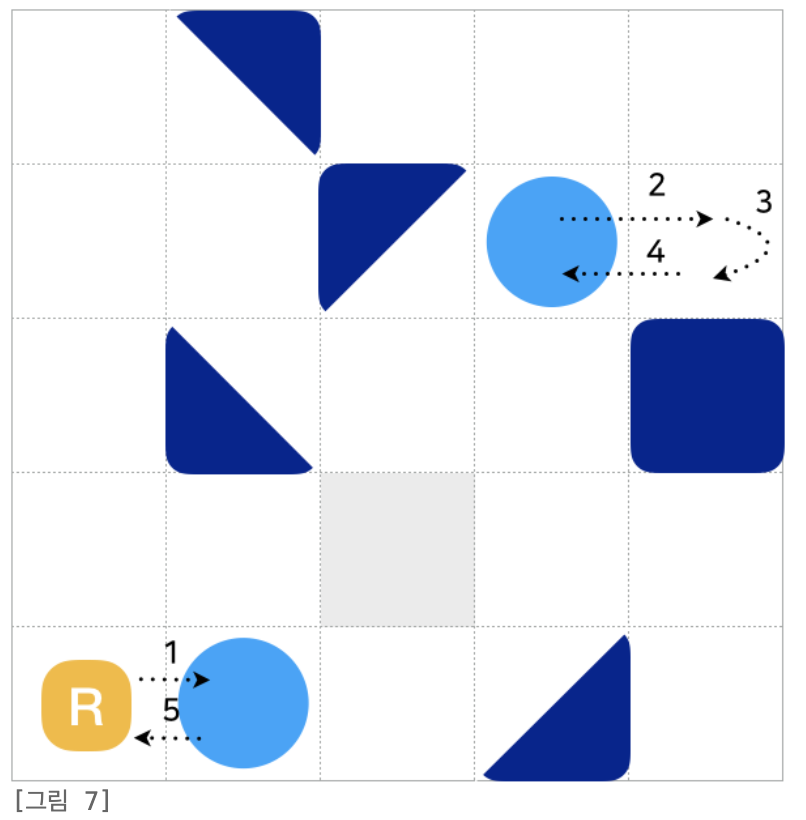
출처 : 알고리즘 잡스

문제 해석 및 해결책

# 로봇 청소기 문제(알고리즘 잡스 제공 문제)
# 문제 velog 링크 : 

#### 문제 파악 (1)
# 로봇 청소기가 있고,
# 그 로봇 청소기의 기능은 only 직진만 가능함(현재 보고있는 방향으로)
# 하지만 여기에 구조물 및 장애물이 있고, 그것에 따라 로봇 청소기의 직진 방향, 경로가 바뀜

# 구조물 및 장애물 종류
# 1) 1~5까지의 구조물은 마주치게되면 방향을 전환시킴
# 2) 6~10번까지의 구조물은 워프라고해서 만나면 같은 숫자로 곳으로 이동시키며(순간이동) 그곳부터 가던 방향대로 가게됨
# ** 이 때 워프를 한다음에 곧바로 다시 워프를 할 수 없음
# 3) 턱이 있는데(-1) 이 턱에 빠지면 운행 정지임

# 결과적으로 로봇을 특정 위치, 특정 방향으로 놓고 작동시킨 다음에 자유자재로 돌아다니게 하고
# 그 다음에 원래 있던 위치 및 방향으로 돌아올 때까지 몇칸을 밟고(청소하고) 돌아왔는지를 체크하며, 그 값의 최대값을 구하라는 문제
# 추가로, 턱에 위치하게 돼도 운행이 끝나므로, 그 때까지 밟은 칸도 최대값이면 정답이 될 수 있음

# 제약 조건 및 주의 사항
# 1) 구조물이 아닌 일반 벽에 부딪히면 직관적으로 뒤도는 방향으로 운행하게 된다
# 2) 워프로 이동한 뒤에 곧바로 워프를 쓸 수 없다. 예를 들어, 워프를 했는데 바로 벽이 있어서 다시 그 워프로 돌아오면 그 워프를 이용못하고 운행 중지가 되는듯!
# 3) 워프는 무조건 한쌍이기 때문에 만약에 7번이 있으면 7번은 하나 더있음(무조건)
# 4) 제자리로 돌아와서 운행이 종료되려면 반드시 그 좌표와 그 방향으로 끝나야한다 
# 5) 칸을 셀 때 구조물 1,2,3,4도 카운트를 하며 워프도 카운트를 각각 해준다(출발지, 목적지) 그러나, 중복해서 계산은 안한다.
# 예를 들어, 특정 칸을 지났다면 돌아올 때 또 밟더라도 중복 카운트 x
# 6) 출발은 구조물, 턱, 벽이 아닌 모든 곳이다. 표기상으로는 0에서만 출발할 수 있음 
# 7) -1인 낮은턱은 밟은 칸으로 카운트하면 안됨!
#### 문제 설계 및 해결책 

# 완전탐색
# 모든 0인 부분에 대해서 동서남북의 방향으로 로봇을 출발시키는 것이다.
# N*N 행렬인데 N은 최대 100이라 했으니 10,000개의 궤적이 있을 것이고,
# 그 만개의 궤적을 최대 만개의 0에 대해서 4방향으로 출발시킬꺼니까... 
# 10000 * 10000 * 4 = 400,000,000 4억개 이상의 시행을 하게 될 것 
# 제한시간이 7초니까 충분히 가능하다

# 만든 배열에 대해서 0인 곳에서만 완전탐색을 실행한다
# 4방향으로 모두 직진시켜보는 것 
# 하나의 dot(좌표)에 대해서 동서남북(for문)으로 직진시켜본다
# 직진 시키다가 장애물을 만나면(혹은 구조물) 그 구조물에 따른 처리를 해준다(워프도 있고)
# 처리를 그렇게 계속 알아서 돌게하다가 -1(턱)을 만나거나 다시 있던 자리로 돌아오면 그 때까지 거쳐온 칸의 수(중복허용x)를 여태까지 최대값과 비교
# 이 때 주의할 사항이
# - 무한 루프를 돌게하는 구간을 어떻게 탐지할 것인가(어떤 곳에 들어갔더니 양옆에 워프 혹은 벽이 있어서 왔다 갔다 빠져나갈 수 없다면)
# - 워프 직후 또 워프가 바로 나오는 것을 어떻게 탐지할지

# 먼저 앞에서부터 주의사항을 제외하고 구현 설계해보면, 

# 먼저 주어진 board를 배열로 만들어야한다.
# 이 때, 경계처리를 해주는게 좋을듯. 벽에 부딪히면 무조건 뒤로 도는 모션을 취할텐데 이를 위해..
# 차라리 경계처리를 5번으로 해주는 것도 좋을듯 5번 자체가 뒤로 돌리는 것이기에 똑같다.
# 경계처리는 길이는 각각1로 해서 5로 해주기
# 그러면 탐색은 (1,1) ~ (n,m)까지 하게 될 것
# + 그리고 여기서 배열을 만들면서 워프의 위치를 찾아서 딕셔너리에 정리하는게 좋을듯
# 예를 들어 6번을 찾았다하면 딕셔너리에
# { 6 : {(x,y):None}} 이렇게 먼저 저장을 하고,
# 그 다음에 또 6이 '분명히' 나올 것이기에 6이 나오면
# { 6: {(x,y):(z,a), (z,a):(x,y)}}이렇게 해놓으면
# 만약에 6을 마주치면 해당 좌표의 값을 이용해서 어디로 워프되는지 알 수 있다.
# board[워프 번호][좌표] => 워프로 넘어갈 좌표
# + 0의 위치를 큐에(배열) 담아두면 그 큐에 있는 좌표에서만 돌려보면 되므로 이것도 받아놓자
# 여기까지 queue에 0의 좌표를 받아뒀고, 워프의 위치 딕셔너리, 주어진 맵을 배열로 만들었다 (1)

# 그럼 하나의 좌표에 대해서 탐색을 하고, 마무리까지 하는 로직을 설계해본다.
# 0 4 0 0 0
# 0 0 3 6 0
# 0 2 0 0 5
# 0 0 -1 0 0
# 0 6 0 1 0

# 테케로 주어진 예시로 해보면
# 먼저 (1,1)에서 동서남북으로 전진해본다
# 1) 전진하는 로직
# 2) 전진하다 장애물을 만났을 때(구조물) 1,2,3,4,5 처리하는 로직
# 3) -1 을 만났을 때 멈추고 최대값과 비교해서 최대값 갱신하는 로직
# 4) 처음 출발한 좌표 및 방향을 만났을 때 멈추고 최대값과 비교해서 최대값 갱신하는 로직
# 5) 워프를 만났을 때 이동하는 좌표로 이동하고 거기서부터 또 직진하게 하는 로직
# 6) 칸을 카운팅하는데 중복되는 칸을 카운트에서 제외하는 로직 

# 1) 전진하는 로직
# ways = [위,오른쪽,아래,왼쪽] 이니까
# ways = [x축-1, y축+1, x축+1, y축-1]
# dx = [-1,0,1,-1]
# dy = [0,1,0,-1]
# 이렇게 해놓고
# board[현재 x좌표 + dx[현재 방향]][현재 y좌표 + dy[현재 방향]]
# 이렇게 하면 현재 방향에서 한칸 전진하는 좌표가 나옴 
# 동서남북 혹은 위아래오른쪽왼쪽인데 x축 +1, -1 y축 +1, -1 이런식으로 갈 것.
# 현재 좌표를 dot = (x,y)라할 때,
# 위쪽은 (x-1,y), 아래쪽은 (x+1,y) 왼쪽은 (x,y-1), 오른쪽은 (x,y+1)
# 이걸 계속해서 반복하니까 while문으로 해놓기

# 2) 전진하다 장애물을 만났을 때 처리하는 로직(1,2,3,4,5)
# 1을 만났을 때 
#   - 오른쪽으로 가는 중이었을 때 : 위쪽으로 방향 전환이 이뤄지고, 위쪽으로 가게됨
#   - 아래쪽으로 가는 중이었을 때 : 왼쪽으로 방향 전환이 이뤄지고, 왼쪽으로 가게됨
#   - 왼쪽으로 가는 중이었을 때 : 벽처럼 뒤돌게됨
#   - 위쪽으로 가는 중이었을 때 : 벽처럼 뒤돌게됨

# 2를 만났을 때 
#   - 오른쪽으로 가는 중이었을 때 : 뒤돌게됨
#   - 아래쪽으로 가는 중이었을 때 : 오른쪽으로 방향전환
#   - 왼쪽으로 가는 중 : 위쪽으로 방향 전환
#   - 위쪽으로 가는 중 : 뒤돌게됨

# 3을 만났을 때 
#   - 오른쪽 : 뒤돌게됨
#   - 아래쪽 : 뒤돌게됨
#   - 왼쪽 : 아래쪽으로 방향전환
#   - 위쪽 : 오른쪽으로 방향전환 

# 4를 만났을 때
#   - 오른쪽 : 아래쪽으로 방향전환
#   - 아래쪽 : 뒤돌게됨
#   - 왼쪽 : 뒤돌게됨
#   - 위쪽 : 왼쪽으로 방향 전환 

# 5 를 만났을 때(벽도 5번)
# 어떤 방향이라도 뒤돌게됨

# 모두다 똑같이 ~할 때가 붙음
# 오른쪽으로 가고 있었을 때 이렇게
# 그러면 현재 가고 있는 방향에 대한 변수가 필요함 heading_to 
# 만약 1을 만났는데 heading_to 가 오른쪽이면 => 위쪽으로 방향이 전환됨
# 이걸 효율적으로 나타내려면...
# 이걸 이렇게 딕셔너리로..?
# 뒤돌기
# {
#     왼쪽: 오른쪽,
#     위쪽: 아래쪽
# }
# 1번 
# {
#     왼쪽 :
# }
# 노가다 같지만 이렇게 해야겠다
# 순서대로 위 오른쪽 아래 왼쪽 = 0123
{ 
    1 : {
        0:2,
        1:0,
        2:3,
        3:1
    }
}

# 이렇게 해두면 만약에 
# 1번을 만나면
# ways[1][heading_to] => 이제 어디로 갈지 방향이 나옴
# 그러면 그 방향을 heading_to 로 갱신해주면 방향이 바뀜 

# 3) -1 을 만났을 때 멈추고 최대값과 비교해서 최대값 갱신하는 로직
# 그러면 여태까지 전진 밑 방향 전환 후 전진 등(구조체를 만났을 때 등)
# 그 칸을 카운트하는 로직을 해놨어야했는데
# 그 로직은 그냥...음 .. set을 이용해서 하자
# set에 튜플 단위의 좌표를 추가하면서 중복되는건 자동으로 없어질테고
# 시작점 좌표 그리고 0을 밟았을 떄, 그리고 구조체 1~4 워프 6~10을 밟았을 때 추가한다 (-1은 추가하지말랬으므로)
# + 5번도 카운트 x임 
# 그렇게 해서 path라는 배열(집합)에 튜플 조합을 모으면서 카운팅하다가
# -1을 만나면 여태까지 max값 (디폴트 -1로 해놓기)과 비교해서 max보다 크면(len(path)가) 갱신 안크면 그대로

# 4) 처음 출발한 좌표 및 방향을 만났을 때 멈추고 최대값과 비교해서 최대값 갱신하는 로직
# 이를 위해 처음 출발한 좌표 및 방향을 미리 저장해둬야함 비교하고 갱신하는 로직은 3번과 동일

# 5) 워프를 만났을 때 이동하는 좌표로 이동하고 거기서부터 또 직진하게 하는 로직
# { 6: {(x,y):(z,a), (z,a):(x,y)}}
# 아까 만들어놓은 이 딕셔너리를 이용하는데
# 만약에 6이나왔다 => warp_dict[6]하면
# {(x,y):(z,a), (z,a):(x,y)} 이렇게 나올 것임
# 그러면 현재 좌표를 b라할 때 warp_dict[6][b]하면
# 그 좌표에서 이어지는 워프 좌표가 나옴 c라하자 
# 그러면 현재 좌표 변수를 now_dot이라할 때 now_dot을 c로 갱신해준다
# 그러면 방향은 그대로 냅뒀으니 다음 시행에서 c부터 원래 향하던 방향으로 직진할 것이다.

# 6) 칸을 카운팅하는데 중복되는 칸을 카운트에서 제외하는 로직
# 집합으로 해결 

## 여기까지 주의사항을 제외하고 로직을 설계해봤고
# 마지막으로 주의사항 관련해서 로직설계
# 주의사항 리스트 

# 1) 구조물이 아닌 일반 벽에 부딪히면 직관적으로 뒤도는 방향으로 운행하게 된다
# 이건 5번과 같은 처리를 하기로 했으니 pass
# 2) 워프로 이동한 뒤에 곧바로 워프를 쓸 수 없다. 예를 들어, 워프를 했는데 바로 벽이 있어서 다시 그 워프로 돌아오면 그 워프를 이용못하고 운행 중지가 되는듯!
# - 무한 루프를 돌게하는 구간을 어떻게 탐지할 것인가(어떤 곳에 들어갔더니 양옆에 워프 혹은 벽이 있어서 왔다 갔다 빠져나갈 수 없다면)
# warp_count를 만들어서 워프를 밟은 즉시 +1 하고
# 이 후에 다른 칸(이 때, 카운트가 안되는 -1, 5는 제외)을 밟을 때 warp_count = 0으로 
# 하지만 곧바로 바로 워프칸을 밟으면 또 count++ 되는데, 그러면 warp_count가 2 이상이된다
# 그런 경우에는 그냥 break..탈수없다고 했으니 이부분은 없는 케이스로 쳐야할 것 같음? 아닌가..(여기 조금 애매함)
# 무한 루프 도는 것..  => 그럴일은 없다 
# 3) 워프는 무조건 한쌍이기 때문에 만약에 7번이 있으면 7번은 하나 더있음(무조건)
# 위의 설계에서 해결
# 4) 제자리로 돌아와서 운행이 종료되려면 반드시 그 좌표와 그 방향으로 끝나야한다 
# 위의 설계에서 해결
# 5) 칸을 셀 때 구조물 1,2,3,4도 카운트를 하며 워프도 카운트를 각각 해준다(출발지, 목적지) 그러나, 중복해서 계산은 안한다.
# 위의 설계에서 해결
# 예를 들어, 특정 칸을 지났다면 돌아올 때 또 밟더라도 중복 카운트 x
# 6) 출발은 구조물, 턱, 벽이 아닌 모든 곳이다. 표기상으로는 0에서만 출발할 수 있음 
# 위의 설계에서 해결
# 7) -1인 낮은턱은 밟은 칸으로 카운트하면 안됨!
# 위의 설계에서 해결


## 1차 구현 결과 에러
# - 문제 파악을 잘못함
# => 만약에 1번을 만났을 때 오른쪽으로 오고있었으면 그부분을 청소조차 하지 못하므로(뒤도는 케이스) 카운트하면 안됨
# 이에 대한 처리가 필요함
# 1~4번에 대해서 뒤돌게 되면 카운트 안하는 처리 필요
# 0~3번 방향이라 했을때 반대로 도는 경우
# 0=2 
# 1=3 
# 2=0
# 3=1
# 이렇게되는데 공통점은 둘의 차이의 절대값이 2이라는 것
# 이걸 이용해서 둘의 차가 절대값 2가 되면 카운트 안하는 로직이 필요할듯

구현 코드

: 구현 코드 깃헙 링크

마무리

: 전형적인 시뮬레이션 문제였던 것 같다. 이런 문제는 정말 한번에 풀어야하고, 한번에 못풀더라도 코드를 간소화해서 에러 핸들링에 유용하도록 해야한다. 잔실수가 일어날 수 있기 때문에 코드 간소화는 항상! 그리고 여기서 내가 썼던 테크닉들은 염두해두자.