프로그래머스 - 멀쩡한 사각형 문제
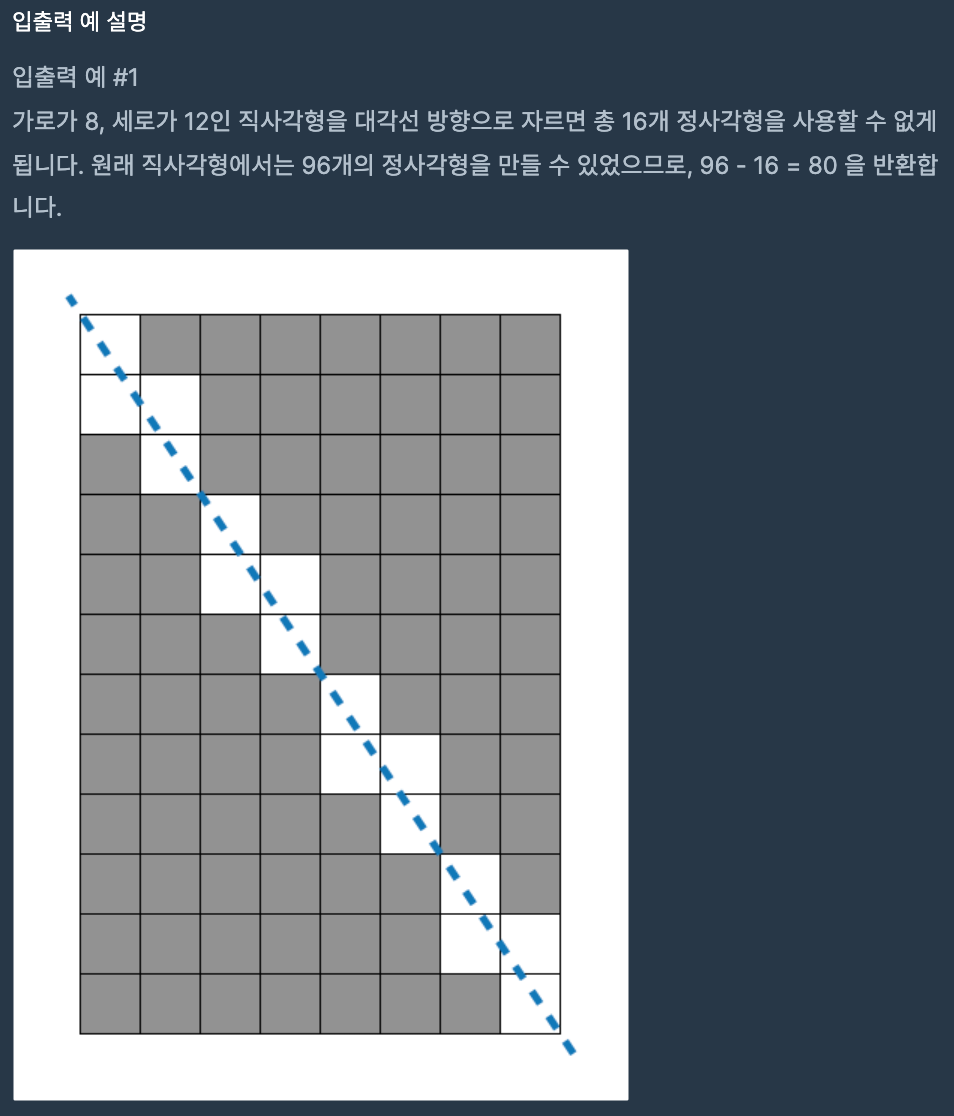
: 결국 스스로 풀지 못하고 힌트 보고서 풀 수 있던 문제. 이런 문제는 솔직히 딱 DP다 DFS다 해서 풀 수 있는 문제라기보다는 어렴풋 보이는 문제의 규칙을 하나하나 헤매가며 풀 수 밖에 없는 문제이기에 그러한 풀이 과정을 따라가보고자 한다. 그래야 다음에도 이런 문제를 만났을 때 포기하기보다는 그 어렴풋 보이는 규칙을 끈질기게 쫓아서 문제를 풀 수 있을테니까!.
문제 풀이
1) 일단 처음 문제 예시를 보고 느낀 점은 확실히 '규칙'이 있다는 점이다. 위에 예시를 보면 2x3 길이의 직사각형 위주로 대각선이 이뤄졌음을 볼 수 있다. 즉, 8x12 길이의 직사각형의 대각선은 2x3 길이의 직사각형 4개와 연관되어 선이 그어진다는 것 정도를 파악할 수 있었다.
2) 그래서 일단 다른 것도 한번 그려봐서 규칙이 실제 있는건지 저 경우에만 저런지 확인해보고자 했다. 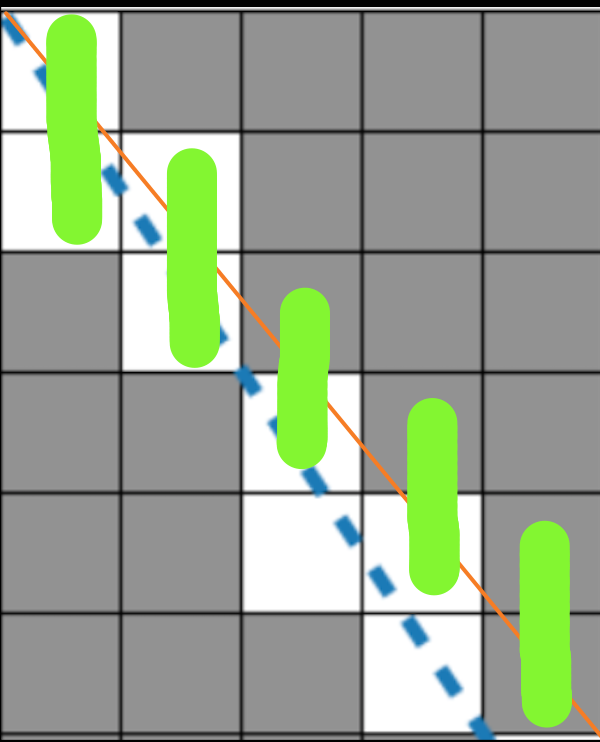
: 그래서 5x6으로 해보니까..흠. 전혀 규칙을 모르겠다. 하지만 처음 예시와 같이 1x2 길이의 직사각형이 또 반복해서 5번 나온 것을 볼 수 있었다. 여태까지 얻은 것은 8x12에서는 2x3 길이의 직사각형 4개(하나에 정사각형 4개가 소모됨)가 대각선에 개입되고, 그에 따라 4x4 = 16개의 정사각형을 못쓰게 된다는 것(1)과 5x6에서는 1x2길이의 직사각형 5개(하나에 정사각형 2개 소모)가 대각선에 개입되고, 그에 따라 5x2 = 10개의 정사각형을 못쓰게 된다는 것을 알았다(2).
3) 이래도 감이 안와서 하나 더해봤다. 이번에는 앞에서 했던 5x6의 두배 크기로 해봤다(10x12). 근데 사실 당연한 결과로 20개가 소모된다. 5x6에서 10개가 소모됐고, 10x12 크기의 직사각형은 그러한 5x6직사각형 4개로 이뤄진 직사각형일테니까!
4) 그러면 결국 앞에서부터 구해본 2x3(1번 케이스), 5x6(2번 케이스) 처럼 더이상 분할할 수 없는 단위에서 정사각형이 몇개 소모되는지를 구할 수 있으면, 그 뒤로는 그 최소 분할 단위로 이뤄진 직사각형들이기에 특정값을 곱해주면 구할 수 있지 않을까? 라는 .. 추상적인 생각까지 발전할 수 있었다.
5) 그러면 일단 최소 분할 단위는 어떻게 구할까. 즉, 더이상 그 안에서 깔끔하게 정리할 수 없는.. 단위?. 점과 점으로 중간에 더이상 이을 수 없는 단위에서 소모되는 정사각형을 구하는 방법만 알면 그래도 정답을 구할 수 있을 것 같은데.. 사실 이 포인트에서 힌트를 봐서.. 내가 풀 수 있는 난이도는 아닌 것 같다는 생각을 했다. 결론적으로 이러한 최소 분할 단위에서 소모되는 정사각형의 개수는 w + h - 1이다. 2x3에서는 2+3-1 = 4, 5x6에서는 5+6-1=10 이렇게 된다.
6) 그러면 최소분할 단위에서 소모되는 정사각형을 알았으니 이제 그 최소 분할 단위로 이뤄진 여러개의 직사각형에서 소모되는 정사각형을 구할 수 있는 규칙을 또 찾아야한다. 여태까지를 보면 8x12 에서 2x3이 최소분할 단위였고, 4개 x 4 = 16개가 됐다(소모되는 정사각형의 개수). 이 때, 4개에 4를 곱해줬는데 이 4는 그러면 뭘까. 더이상 나눌 수 없는 단위라고 생각해서 유추해봤을 때 최대공약수를 떠올릴 수 있었다(이건 실제로 그냥 직관적으로 떠오른 것이라.. 설명이 불가하다). 그래서 10x12의 케이스에도 적용해보면, 10과 12의 최대 공약수는 2다. 또한 최소분할 단위에서 소모되는 정사각형은(5+6-1) 10이다. 그래서 최종적으로 소모되는 정사각형 개수는 10x2=20이다.
7) 결론적으로 특정 w x h길이의 직사각형에서 소모되는 정사각형의 수는 w,h의 최대공약수를 기준으로 둘을 나눠주고, w//gcd, h//gcd => 이 최소 분할 단위에서 소모되는 정사각형을 구해서 '(w//gcd) + (h//gcd) -1' 이 개수에다가 최대공약수를 곱해주면 최종적으로 소모되는 정사각형의 개수를 구할 수 있다. 근데 이 공식을 간략하게 정리하면
((w//gcd) + (h//gcd) -1) * gcd = w+h-gcd
가 되므로 결과적으로 최종적으로 남는 정상적인 정사각형의 개수는 방금 구한 소모되는 공식을 통해 구한 소모된 정사각형의 개수를 전체(처음 정사각형 개수) 개수에서 빼주면 된다.
8) 최종 공식은
w x h - (w+h-gcd)
이 된다. 근데 이 때, w,h가 1억이하의 자연수라고 했으므로 완전 탐색 방법의 gcd 구하는 로직은 비효율적이기에(시간 복잡도 초과) 유클리드 호제법으로 최대공약수를 구해준다.
최종 풀이 코드
def solution(w,h):
answer = None
if w>h:
a = w
b = h
else:
a = h
b = w
while True:
r = int(a % b)
if r == 0:
break
a = b
b = r
answer = (h * w) - (h+w-b)
return answer
추가적으로 math 모듈을 이용해서 푼 코드(좀 더 간결함)
import math
def solution(w,h):
answer = None
b = math.gcd(w,h)
answer = (h * w) - (h+w-b)
return answer
코멘트
: 중간에 w+h-1이 최소분할 단위의 직사각형에서 소모되는 정사각형의 개수의 공식이라는 것을 캐치하려면 어떻게 해야할지는.. 모르겠다. 이건 이론이 아니라 센스, 경험에서 오는 직관이니까.. 이런 문제에 적응해 나아가는 수밖에 없을듯..!
