동적 계획법과 관련된 연속 부분 최대합 문제 풀기
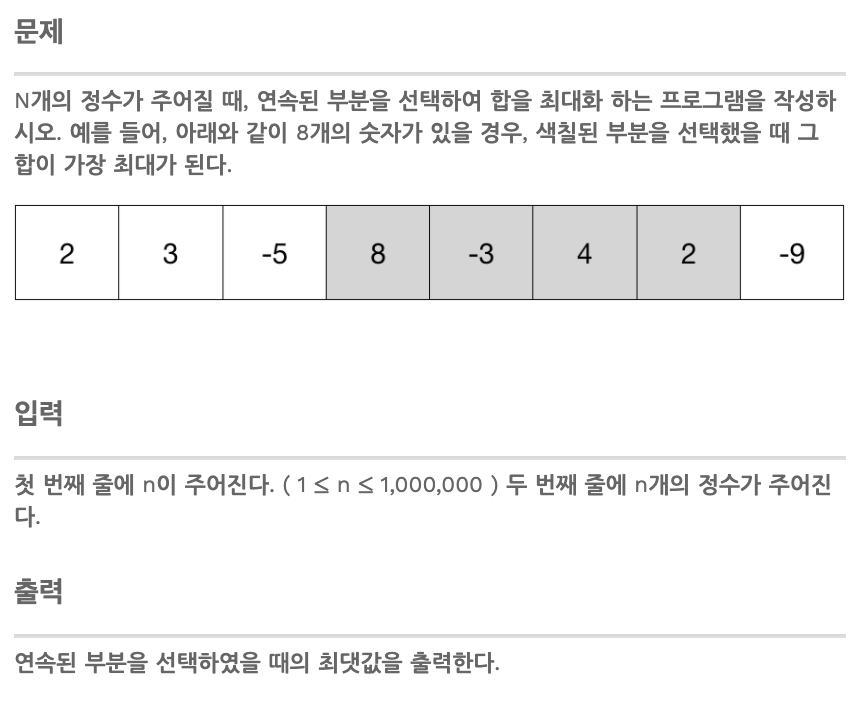

: 이전에 이문제를 분할정복법, 완전탐색법 이렇게 두가지 방법으로 풀어본적이 있는데 오늘은 이 문제를 '동적계획법'을 써서 풀어보고자 한다. 이렇게 보면, 동적계획법은 일종의 규칙을 찾아내서 푸는 방법인 것 같고, 나머지는 완전탐색법 -> 좀 더 효율적인 완전탐색법 이런식은 아닌가 생각이든다(3가지를 놓고 봤을 때 주관적인 생각).
문제 이해하기
: 이 문제는 많이 풀어본 유형이기에 간단하게 문제를 설명해보면, 문제 이름과 같이 순열(숫자의 나열)을 받아서 그 숫자들을 가지고, 이 때, 연속된 숫자를 가지고 만들 수 있는 최대값을 구하라는 문제이다.
동적계획법으로 접근하기
: 분할정복법을 이용하면 NlogN이기에 n이 최대 백만이어도 풀 수 있지만, 이번에는 동적계획법 풀이로 풀어보고자 한다(완전 탐색법으로는 시간복잡도에 의해 풀 수 없다).
1) 무엇을 구할지를 정의한다(부분 문제를 정의한다).
: 이 과정에서는 예제로 주어진 케이스를 가지고, 어떤 규칙을 찾아내야하는데, 그 과정에서 주로 쓰이는 것을 팁처럼 적용해보면, '유형화'를 해보는 것이다. 예를 들어, 이 문제의 예제를 가지고 이 문제에서 유형화를 해보면
2 3 -5 8 -3 4 2 -9
에서 연속된 수의 합의 최대값을 구하려면
완전탐색의 관점에서는 길이 1, 2, 3, 4. ... 길이만큼의 연속된 수를 모두 탐색하면서 최대값을 구하면 된다. 하지만, 이 문제를 분할 혹은 좀더 세분화해본다면 '각각의 요소를 끝으로 하는 연속된 수에서 최대값을 구해보자' 라는 생각으로 접근해볼 수 있다. 무슨말인가하면, 첫번째 요소인 2를 끝으로 하는 연속된 수에서 최대값은 2이다. 그럼 3을 오른쪽 끝으로 하는 연속된 수에서의 최대값은 5이다. 똑같이 -5를 끝으로하는 연속된 수의 최대값은 0이다. 이런식으로 끝요소까지 구해보면 결국 여태까지 구한 최대값 중에 최대값 하나가 이 전체 요소를 연속해서 만들 수 있는 최대값이라는 것을 알 수 있다.
2 3 -5 8 -3 4 2 -9 2를 오른쪽 끝으로 하는 연속된 수 : 2밖에 없으므로 2가 최대 [2] 3을 오른쪽 끝으로 하는 연속된 수 : 2+3 > 3 이므로 5가 최대 -5를 오른쪽 끝으로 하는 연속된 수 : 2+3-5 > 3-5 > -5 이므로 0이 최대 8을 오른쪽 끝으로 하는 연속된 수 : 8>=2+3-5+8>3-5+8>-5+8 이므로 8이 최대 ...... 2를 오른쪽 끝으로하는 연속된 수 : 11가 최대 -9를 오른쪽 끝으로 하는 연속된 수 : 2가 최대
: 이렇게 직접 해보다보면 규칙을 찾아낼 수 있다. 하지만 여기서 우리가 처음에 '유형화'했던 작업인 ~를 오른쪽 끝으로 하는 연속된 수 중에 최대값을 구하는 것을 우리가 정의할 문제, 즉, 부분 문제를 정의하는 것으로 떠올리는 것은 이런 문제를 많이 접해봐야 떠오르는 것 같다.. 어쨌든 부분문제를 정의해보면 'i를 오른쪽 끝으로 하는 연속된 수중에 최대값을 구하는 것' 이라고 할 수 있을 것 같다. 그래서 실제로 그것을 구하기 위한 식(점화식)을 세워보면, 다음과 같다.
2) 점화식 세우기(계산을 위한 식세우기)
:
T(i) = Max(T(i-1), i번째 요소)
이렇게 짜볼 수 있다. 그 이유는 위에 우리가 유형화하면서 구해봤던 로직을 따라가보면 알 수 있는데,
i번째 요소를 오른쪽 끝으로 하면서 연속된 수의 최대값을 구하면서 알 수 있는건, i-1번째의 최대값을 구하면, 그 다음인 i번째 요소까지의 최대값은 그 앞인 i-1번째의 최대값에 현재 i번째 요소를 더한값 or 더하지 않은 값 둘중 하나가 된다는 것이다. 예를 들어,
2를 오른쪽 끝으로 하는 연속된 수 : 2밖에 없으므로 2가 최대 [2] 3을 오른쪽 끝으로 하는 연속된 수 : 2+3 > 3 이므로 5가 최대 -5를 오른쪽 끝으로 하는 연속된 수 : 2+3-5 > 3-5 > -5 이므로 0이 최대 8을 오른쪽 끝으로 하는 연속된 수 : 8>=2+3-5+8>3-5+8>-5+8 이므로 8이 최대
여기를 보면, 3을 오른쪽 끝으로 하는 연속된 수중에 최대값은 앞까지의 최대값인 2+3 이거나 3일수밖에 없다. 앞까지의 연속된 최대값은 이미 앞에서 정해졌기에 현재 요소를 더할지 말지만 결정하면 되는 것이다. 만약에 3이 아니라 -4였다면 더하지 않는 것이 유리할 것이기 때문이다. 이런 로직을 따르면 위와 같은 점화식이 나오게 되고, 결론적으로
3) 실제 코드 구현하기

: 이렇게 코드를 써서 풀어볼 수 있겠다.
마무리 및 코멘트
: 위와 같은 방식으로 문제를 풀면 사실상 O(N)의 시간복잡도를 문제를 풀 수 있다. 분할정복법인 O(NlogN)보다도 빠른 시간복잡도이기에 동적계획법의 효과(?)를 알 수 있는 부분이다. 아직 동적계획법에 익숙치 않지만, 여기까지 내가 느끼는 바는 동적계획법은 일단 완전탐색법으로 풀리지 않는다 했을 때 고려해봐야할 선택지이고, 만약 동적계획법을 시도해보고자 한다면, 먼저 예제를 가지고 직접 문제에서 요구하는 것을 해보되, '유형화' 해보는 자세가 필요한 것 같다. 끝을 i로 하는 연속된 수의 최대값을 구해보자라는 아이디어가 툭하고 튀어나지는 않겠지만, 이처럼 1)뭔가를 유형화해서 혹은 분할해서 생각해보는 아이디어부터 시작해야할 것 같고, 그 다음에는 2)이전의 자기 자신을 가지고, 현재의 자기 자신을 구할 수 있다는 발상을 끊임없이 유지해야한다는 것이다(피보나치 수열처럼). 또한, 이것은 어떤 외워야할 공식 같은게 아니다. 동적계획법은 설계단계에서 떠올라야할 일종의 아이디어지 이것을 연속부분 최대합 문제 자체를 외워서 이런 유형이 나올 때까지 기다리면서 외워둬야할 공식 같은 것이 아니라는 것!.
