재귀함수 및 수학적 귀납법에 대한 정리
재귀함수(recursive function)
:간단하게 재귀함수에 대해서 정의를 해보면,
재귀함수는 '자신을 통해서 자신을 구하는 함수'라고 할 수 있다.
흔히 재귀함수 관련해서 러시아 인형(?)을 얘기하는 것도 이러한 맥락인데
하나의 러시아 인형이 존재(?)하기 위해서 그 안에 겉에서는 보이지 않는 수많은 다른 러시아 인형들이
겉으로 보이는 하나의 러시아 인형의 존재를 보증(?)해준다.
너무 어려운 예시인 것 같고..ㅎ

간단하게 팩토리얼을 구하는 (N!) 함수를 통해 알아보면,
위의 함수는
n을 인풋으로 넣었을 때 n! 값을 리턴해주는 함수이다.
이 때, 사실 n! 은 '순차적 계산법'을 통해서 구할 수도 있다.
순차적 계산법이란?
여태까지 대부분의 알고리즘 문제를 풀 때 적용했던 것으로
말그대로 순차적으로 계산을 해서 결과를 도출하는 계산법이다.
예를 들어,
3!을 순차적 계산법으로 구해보면,
먼저,
3에 2를 곱하고,
그 결과값인 6에 마지막으로 1을 곱해주는 방법으로 3!을 구하는 것이다.
그렇다면 여기서 귀납적 계산법을 쓰면 어떻게될까?
귀납적 계산법은 계산을 할 때 자기 자신을 사용해서 자기 자신을 구해내는 계산법(?)이라고 할 수 있다.
예를 들어,
3!을 구할 때
3! = 2! 3
이라고 해보면,
우리는 쉽게 2!이 21이므로 저것이 맞는 것임을 알 수 있다.
그러나 만약 2!이 2임을 모른다면
2!이 참임도 증명을 해야한다.
그럼 2!은 ?
2! = 1! * 2 그럼 1!은?
1! = 1
아하..
맨 끝에 닿으니까 1!=1이라는 명확한 결과가 나왔다
(물론 2!이 2인 것도 평소 많이 봤던 우리들에겐 명확하지만)
그러면
1! = 1이라는 것을 통해
2! = 1!2 임이 확실해지고
2! = 1!2 = 2 임을 통해
3! = 2! 3 = 6임이 확실해졌다.
그런데 생각해보면
결국
'n! = n (n-1)!' 을 알기위해
(n-1)! 을 구해보고, 그것을 알기위해 그 이전.. 해서 결국 명확한 1!=1까지 갔던 것이다.
하지만 위에서 n!을 구할 때 (n-1)!이 이미 맞다고 가정하고
n!을 구하면? 즉, 굳이 1!=1까지 안가보고
(n-1)!이 (n-1) (n-2)!이라는 것을 가정하고 구해보면
n! = n (n-1)!
(n-1)!은 1부터 n-1까지의 수를 곱한 것이라고 가정하고 시작하면
n! = n * (n-1)! 임은 명확해진다.
여기서 자기 자신을 활용하여 자기 자신을 구한다는 귀납적 계산법의 형태를 볼 수 있다.
또한, 이런식으로 이전의 경우를 명확하다고 가정하고 그 다음 경우를 증명하는(참인지 거짓인지 판단) 방법을
'수학적 귀납법' 이라고 한다.
그렇다면 다시 팩토리얼 함수로 돌아와서 다시보면
팩토리얼 함수 자체가 수학적 귀납법의 모습을 띄는 것을 알 수 있다.
factorial(n)이 n!이라는 것을 리턴해줄 것이라고 생각하는데
그 근거는 factorial 함수의 return 문에
factorial(n-1) 이 (n-1)!을 잘 리턴해줄 것이라는 '가정'이 숨어있기 때문이다.
위에서 수학적 귀납법은
이전의 경우가 명확하다고 가정하고, 다음 경우를 증명하는 것이라고 했는데, 이 함수 자체가 수학적 귀납법의 형태로 만들어진 것을 알 수 있다.
여기서 우리는 (n-1)!을 증명하는 것을 또 그 이전 factorial(n-2)가 잘 작동한다는 것에 맡기고
그냥 최종 factorial(n)을 구하는 방향으로 나아간다.
즉, 러시아 인형이 하나하나 열어지듯이
끝까지 가보면, 분명히 마지막 러시아 인형이 있을 것이지만,
그리고 그 마지막 러시아 인형이 외적으로 보이는 하나의 러시아 인형의 존재를(?) 확증해주겠지만
일단 그 끝까지 안열어보고
그 바로 이전 인형이 확실히 존재한다는 가정 하나로 제일 최신의 러시아 인형의 존재를 확증하는 것이다..
(이건 나만의 비유인걸로...ㅎ)
하지만, 만약 호기심이 많고, 회의적인 사람이 factorial(n-1)이 잘작동하는지는 어떻게 알지? 하면?
factorial(n-2)가 잘작동하니까 ㅎ 라고 하면 된다.
그러면 또, factorial(n-2)가 잘 작동하는지 어떻게 알지?
=> factorial(n-3) is okay..!
=> .....
=> .... => ... factorial(1) = 1 !
결국 맨 끝에가서

factorial(1) =1이라는 '정의'가 나타나고,
이로 인해
factorial(1+1)
factorial(2+1)
=> factorial(n-1) => factorial(n) 까지 확실해지게 된다.
이 때,
factorial(1)이 1이되는 것은 어떻게 증명할건데? 하면
이건 '정의'이기 때문에 증명할 필요가 없는 명제라고 할 수 있다.
그렇다면 이러한 factorial함수 예제로 봤을 때
재귀함수는 이러한 특징을 갖는다.
먼저,
첫번째 return에서
자기 자신을 호출하면
그 return문은 자기 자신을 호출한 부분의 함수(또다른 스코프)가 끝날 때까지
일종의 기다림(?), 대기를 하게 된다.-- 특징1
그러면 그 다음 함수도 똑같이 자기 자신을 활용한 return이 있을 것이기에 대기하게되고
결국 끝까지가서
일종의 break문인 if절을 만나(factorial(1)에서) 최종적으로 1을 리턴하게 되고,
(이렇게 일종의 break문 위의 개념상의 표현으로는 증명이 필요없는 정의와 같은 것이 있는 것이 특징2)
그 1이 바로 위 스코프로 대기중인 factorial(2)의 return문에 들어가게 되고,
factorial(2)도 리턴을 하게되고.. 이렇게 연쇄적으로
리턴을 하게되면서 최종적으로 factorial(n)의 값이 리턴되게 된다.
여기까지 factorial함수로 재귀함수에 대해서 이론적인 부분을 살펴봤는데, 좀더 공부해야 명확해질 것 같다..ㅎ
어쨌든
포인트는
재귀함수는
1) 자기 자신을 활용한 함수(다른 스코프)가 끝날 때까지 대기를 한다.
2) 결국 더이상 대기를 할 필요가없는 break문이 있다.
수학적 귀납법은
1) f(n)을 구하기 위해 f(n-1)이 맞다고 가정한다.
2) 실제로 하나하나 캐물어가다보면 결국 증명할 필요가없는 최종 정의가 있고, 이것이 나머지를 확증시킨다.
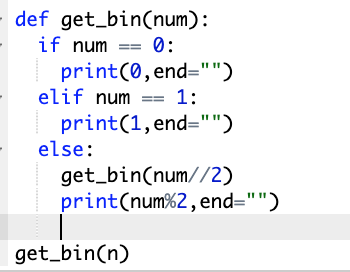
재귀함수를 이용한 문제풀이
n을 입력받고
n에 대한 이진수를 리턴하는 함수를 만들어보자