백준 - 드래곤 커브 / Gold 4 / 15685번 / Python

문제 📋

백준 - 드래곤 커브

풀이 📝

import sys


def solution(N, curves):
    answer = 0
    direction = [(0, 1), (-1, 0), (0, -1), (1, 0)]
    is_in_curve = [[False] * 101 for _ in range(101)]

    for curve in curves:
        col, row, way, gen = curve
        points = [(row, col)]
        delta_row, delta_col = direction[way]

        points.append((row + delta_row, col + delta_col))

        while gen > 0:
            axis = points[-1]  # 끝점이 회전축

            for i in range(len(points)-2, -1, -1):  # 끝점을 제외하고 모든 점들을 270도 회전변환 수행.
                row, col = points[i]
                row -= axis[0]  # 원점으로 이동
                col -= axis[1]

                temp = row  # 원점기준 270° 회전변환 수행.
                row = col  # X' = cos 270°X - sin 270° Y = Y
                col = -temp  # Y' = sin 270° X + cos 270° Y = - X

                row += axis[0]  # 다시 원래 위치로 이동.
                col += axis[1]
                points.append((row, col))
            gen -= 1

        for point in points:
            row, col = point
            is_in_curve[row][col] = True

    for i in range(100):
        for j in range(100):
            square = [(i, j), (i+1, j), (i, j+1), (i+1, j+1)]
            is_square = True

            for row, col in square:
                if not is_in_curve[row][col]:
                    is_square = False
                    break

            if is_square:
                answer += 1

    return answer


N = int(sys.stdin.readline())
curves = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]

print(solution(N, curves))

조금 어려웠던 구현 문제이다.
가장 중요한 부분은 드래곤 커브를 구현하여 점들의 위치를 추적하는 부분이다.

다른 여러 풀이들을 보면 드래곤 커브를 나열해 보면서 패턴을 찾아내는 풀이가 많았다.
좋은 풀이라고 생각한다.

하지만 만약 패턴이 보이지 않다면 어떻게 할 것인가?
풀이를 포기해야 할까?

아니다 이 문제는 구현 문제이다.
패턴이 보이지 않더라도 풀 수 있어야 한다.

그래서 일부러 문제가 제시하는 그대로 구현하여 풀이를 진행했다.

끝점을 기준으로 시계방향으로 90° 회전시키라는 의미는
끝점을 기준으로 270° 회전변환을 수행하라는 의미이다.
회전 변환을 원점 기준으로 수행할 때 공식은 다음과 같다.

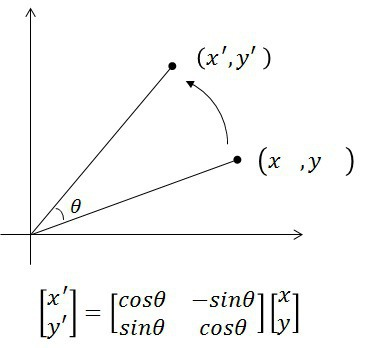
따라서 드래곤 커브의 새로운 점들 다음과 같이 생성된다.

1. 끝점에서 원점으로 평행이동.
2. 원점 기준으로 270도 회전변환.
3. 다시 끝점으로 평행이동.