백준 - 숨바꼭질 / Silver 1 / 1697번 / Python

문제 📋

백준 - 숨바꼭질

풀이 📝

import sys
from collections import deque


def delta_x(x):
    return [2 * x, x + 1, x - 1]


def solution(n, k, max_x):
    time = 0
    visited = [False] * (max_x + 1)
    q = deque([n])

    while q:
        for _ in range(len(q)):
            cur = q.popleft()

            if cur == k:
                return time

            for new_x in delta_x(cur):
                if 0 <= new_x <= max_x and not visited[new_x]:
                    q.append(new_x)
                    visited[new_x] = True
        time += 1
    return -1


n, k = map(int, sys.stdin.readline().split())
print(solution(n, k, 100000))

동생과 수빈이의 위치가 주어지고 수빈이가 X+1, X-1, 2*X 과 같이 이동할 수 있을 때
동생을 찾는데 걸리는 최소시간을 찾는 문제이다.

먼저 이 문제를 그래프 탐색 문제로서 정의해봤다.
그렇게 되면 탐색할 그래프는 X가 루트 노트이고
X-1, X+1, 2*X 가 자식 노드로서 반복 되는 트리 형태를 떠올릴 수 있다.

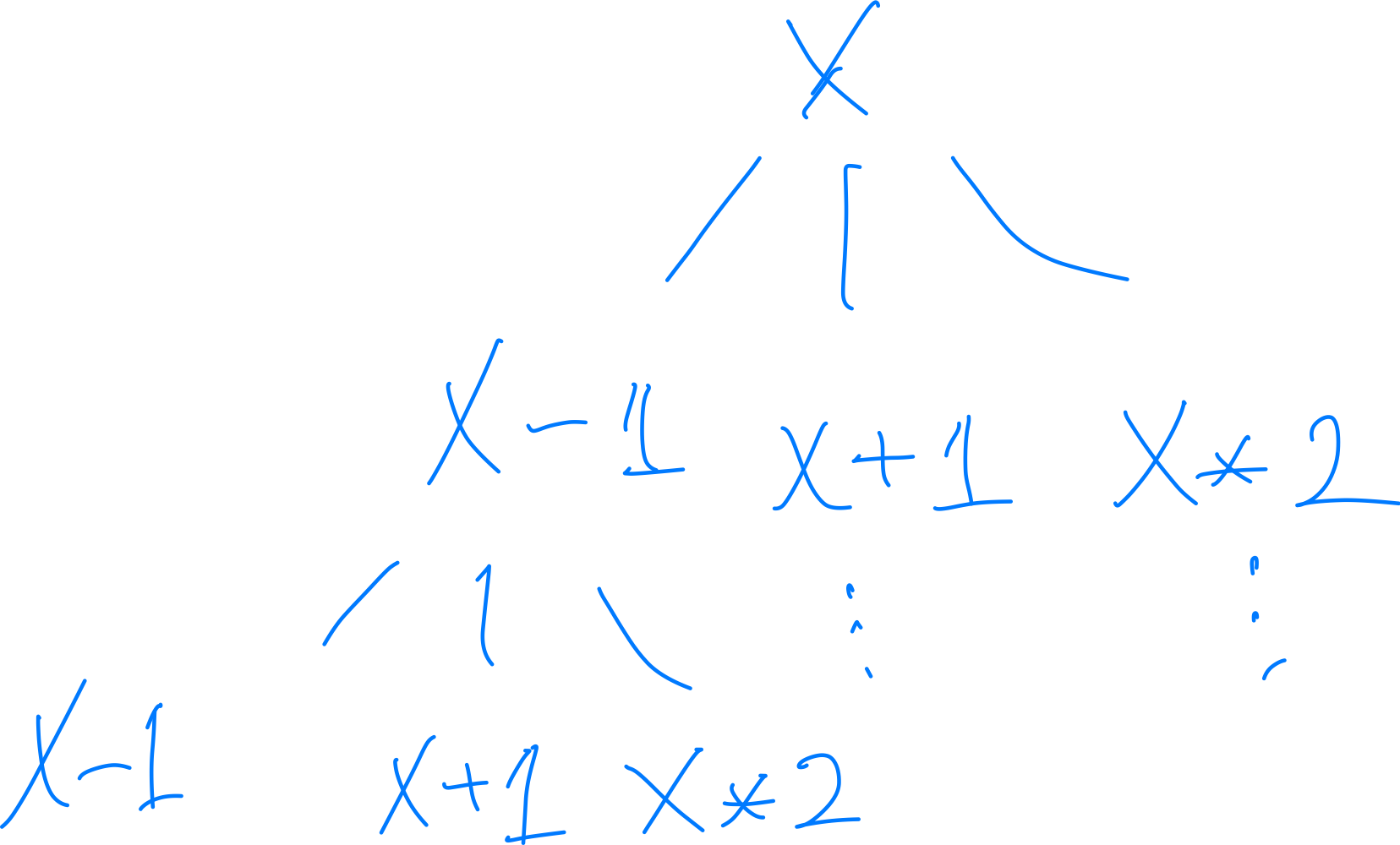
그런 다음에 동생의 위치와 값이 같으면서 가장 가까운 노드를 찾아야 하기 때문에
최단거리 문제이고 따라서 BFS를 사용하여 한 Depth씩 차례대로 탐색해 답을 찾았다.