Programmers js - 소수 찾기

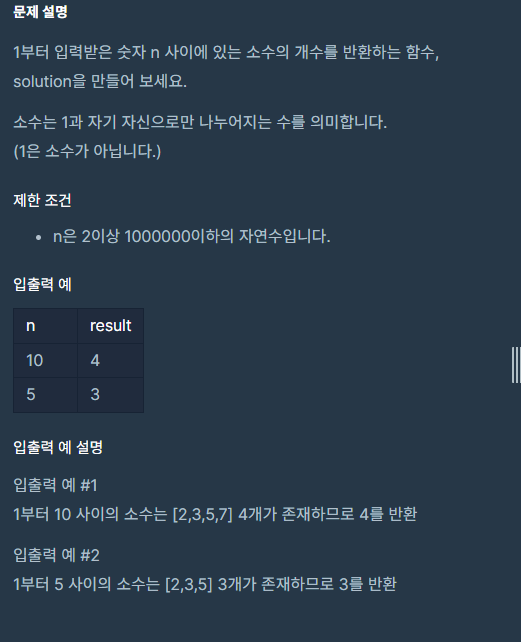
내 처음 코드는 아래와 같다.

function solution(n) {
    var answer = 0;
  for(let i = 2; i <= n; i++ ){
      if(isPrime(i)) answer+=1
  }
    
    
    return answer
}

function isPrime(n) {
    for(let i = 2 ; i <= Math.sqrt(n) ; i++){
        if(n % i === 0)  return false 
    }
    return true
}

테스트 케이스는 통과하였지만 효율성의 문제에서 고꾸라져서 어떻게 하나 찾아보던 와중 소수를 찾는 알고리즘인 에라토스테네스의 체를 보게되어 옛날에 알던 수학적 지식이기에 해당 코드를 이해하며 다시 작성해보았음.

function solution(n) {
    if (n < 2) return 0;

    let isPrime = Array(n + 1).fill(true);

    isPrime[0] = isPrime[1] = false;

    for (let i = 2; i <= Math.sqrt(n); i++) {
        if (isPrime[i]) {
            for (let j = i * i; j <= n; j += i) {
                isPrime[j] = false;
            }
        }
    }
    let answer = isPrime.reduce((acc, val) => acc + val, 0);

    return answer;
}

완벽히 내가 풀어낸 코드는 아니기에 아쉬움이 있지만 true + true는 2인 것과 이렇게 소수를 찾아낼 수 있다는 점 그리고 위와 같은 배열 생성 방식을 다시 상기할 수 있어서 좋은 문제였다.