[python] 백준 1002번 - 터렛

희희구리·2023년 4월 21일

백준

목록 보기

13/21

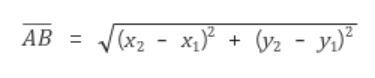
문제

조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다.

이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.

조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.

링크 참조

https://www.acmicpc.net/problem/1002

풀이 설명

처음 생각했던 아이디어는 원의 방정식으로 X,Y 중 정수 쌍을 구해보려 하였다.
그렇게 하게 되면 모든 정수 내에서 구해야 하기 때문에 굉장히 코드가 복잡해질 것 같았다.

그래서 조금 다르게 생각해본 것은 삼각형으로 푸는 것이었다.

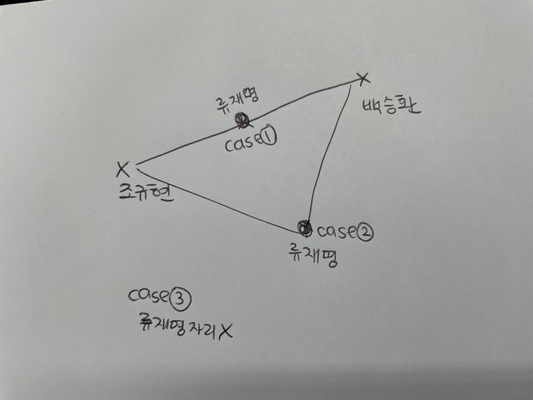
case은 크게 3개로 나눴다.

류재명이 조규현과 백승환 사이에 있는 경우.
1-1. 조규현과 백승환이 같은 곳에 위치하면 류재명은 무한 값을 가짐
류재명이 조규현과 백승환과 삼각형을 이루고 있는 것과 같은 경우
류재명이 조규현과 백승환의 거리를 이룰 수 없는 경우

코드

N = int(input())

for _ in range(N):
    x1,y1,r1,x2,y2,r2 = map(int,input().split())
    
    Joe_Baek = (((x1-x2)**2)+((y1-y2)**2))**(1/2)
    distance = [r1,r2,Joe_Baek]
    maxValue = max(distance)
    distance.pop(distance.index(maxValue))
    remain = sum(distance)
    
    if maxValue < remain:
        print(2)
    elif maxValue == remain:
        if x1 == x2 == y1 == y2:
            print(-1)
        else:
            print(1)
    else:
        print(0)