Dijkstra
: 그래프에서 하나의 고정된 노드로부터 다른 노드로의 최단경로를 구하는 탐색 알고리즘 ( 음의 가중치 없을 때만 사용 가능 → 음의 가중치의 경우, 벨만-포드 알고리즘 )
※ dp 활용
과정
- 방문하지 않은 정점 중 가장 가중치 작은 정점을 방문한다. (처음에 시작 정점 방문)
- 해당 정점을 거쳐서 갈 수 있는 정점의 거리가 이전에 기록한 값보다 작다면 그 거리를 갱신한다.
예시
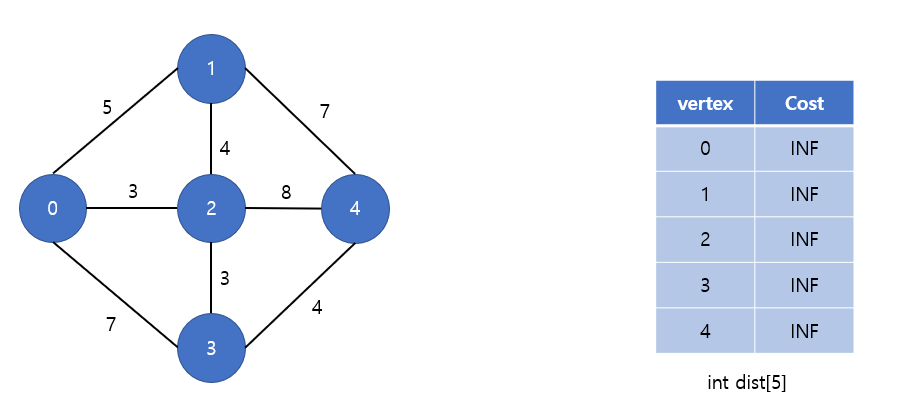 배열 dist[] INF로 초기화 후, dist[]에 각 정점까지의 최단거리를 갱신해 나갈 것이다.
배열 dist[] INF로 초기화 후, dist[]에 각 정점까지의 최단거리를 갱신해 나갈 것이다.
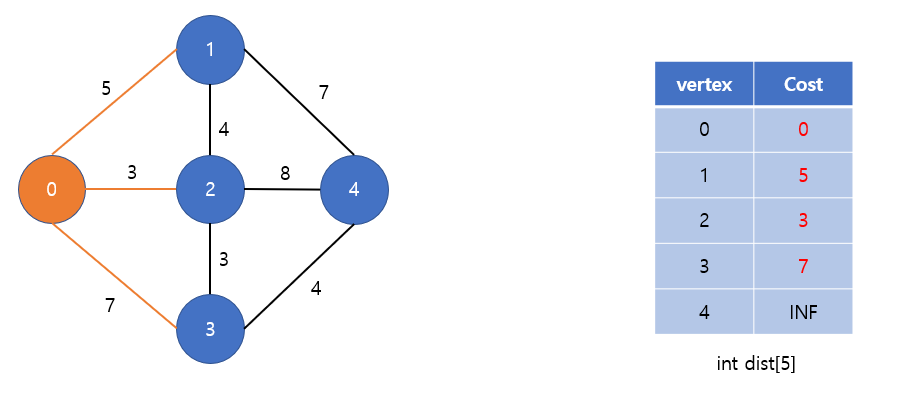 시작점 0 방문 후, 0에서 방문할 수 있는 정점들에 대한 거리를 갱신한다.
시작점 0 방문 후, 0에서 방문할 수 있는 정점들에 대한 거리를 갱신한다.
 아직 방문하지 않은 정점 중, 가장 가중치가 작은 2번 정점을 방문한다.
아직 방문하지 않은 정점 중, 가장 가중치가 작은 2번 정점을 방문한다.
0→2→3 : 6 < dist[3]=7 이므로 최단거리 갱신
0→2→4 : 11 < dist[2]=INF 이므로 최단거리 갱신
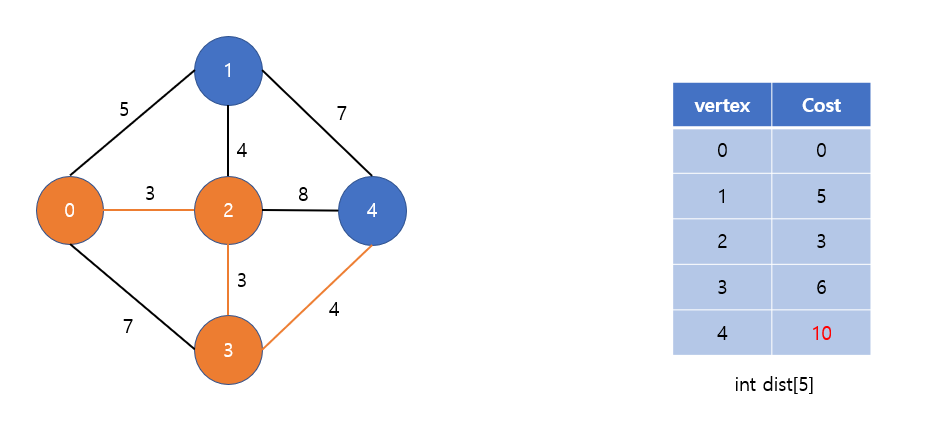 아직 방문하지 않은 정점 중, 가장 가중치가 작은 3번 정점을 방문한다.
아직 방문하지 않은 정점 중, 가장 가중치가 작은 3번 정점을 방문한다.
0→2→3→4 : 10 < dist[4]=11 이므로 최단거리 갱신
 아직 방문하지 않은 정점 중, 가장 가중치가 작은 4번 정점을 방문한다.
아직 방문하지 않은 정점 중, 가장 가중치가 작은 4번 정점을 방문한다.
갱신할 거리가 없다.
 아직 방문하지 않은 정점 중, 가장 가중치가 작은 1번 정점을 방문한다.
아직 방문하지 않은 정점 중, 가장 가중치가 작은 1번 정점을 방문한다.
갱신할 거리가 없다.
모든 정점을 방문했으므로 종료한다.
구현
priority_queue를 사용하여 구현 : O(ElogV)
#include<bits/stdc++.h>
#define MAXV 20001
#define MAXE 300001
#define INF 1000001
using namespace std;
struct info {
int node, w; // 노드, 누적 거리
info() {};
info(int node, int w) :node(node), w(w) {};
bool operator <(const info i) const { // 오름차순
return w > i.w;
}
};
int v, e, k;
vector<info> g[MAXV];
int ans[MAXV];
bool check[MAXV];
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e >> k;
for (int i = 0, u, v, w; i < e; i++) {
cin >> u >> v >> w;
g[u].push_back(info(v, w)); // u -> v 방향그래프
}
for (int i = 0; i <= v; i++) {
ans[i] = INF;
}
priority_queue<info> pq;
ans[k] = 0;
pq.push(info(k, 0));
while (!pq.empty()) {
info cur = pq.top();
pq.pop();
if (check[cur.node]) continue; // true인 경우 건너뛰기
check[cur.node] = true;
for (int i = 0; i < g[cur.node].size(); i++) {
int nxt_n = g[cur.node][i].node;
int nxt_w = g[cur.node][i].w;
if (nxt_w + ans[cur.node] < ans[nxt_n]) { // 최솟값으로 갱신
ans[nxt_n] = nxt_w + ans[cur.node];
pq.push(info(nxt_n, ans[nxt_n]));
}
}
}
for (int i = 1; i <= v; i++) {
if (ans[i] == INF) cout << "INF\n";
else cout << ans[i] << "\n";
}
return 0;
}
