[Algorithm/C++] Segment Tree (Top down)

Segment Tree

"구간을 저장하기 위한 트리"
→ 여러 개의 데이터가 연속적으로 존재할 때, 특정한 범위의 데이터의 합을 구하는 방법

---

Segment Tree 사용하는 문제

1. 구간 l, r (l ≤ r)이 주어졌을 때, A[l] + A[l+1] + ... + A[r-1] + A[r]을 구해서 출력하기
2. i번째 수를 v로 바꾸기. A[i] = v

총 시간 복잡도 : O(lgN)

---

Tree 구성

• Leaf 노드: 배열의 수 자체
• 다른 노드: 왼쪽 자식과 오른쪽 자식의 합 저장

ex) N = 10
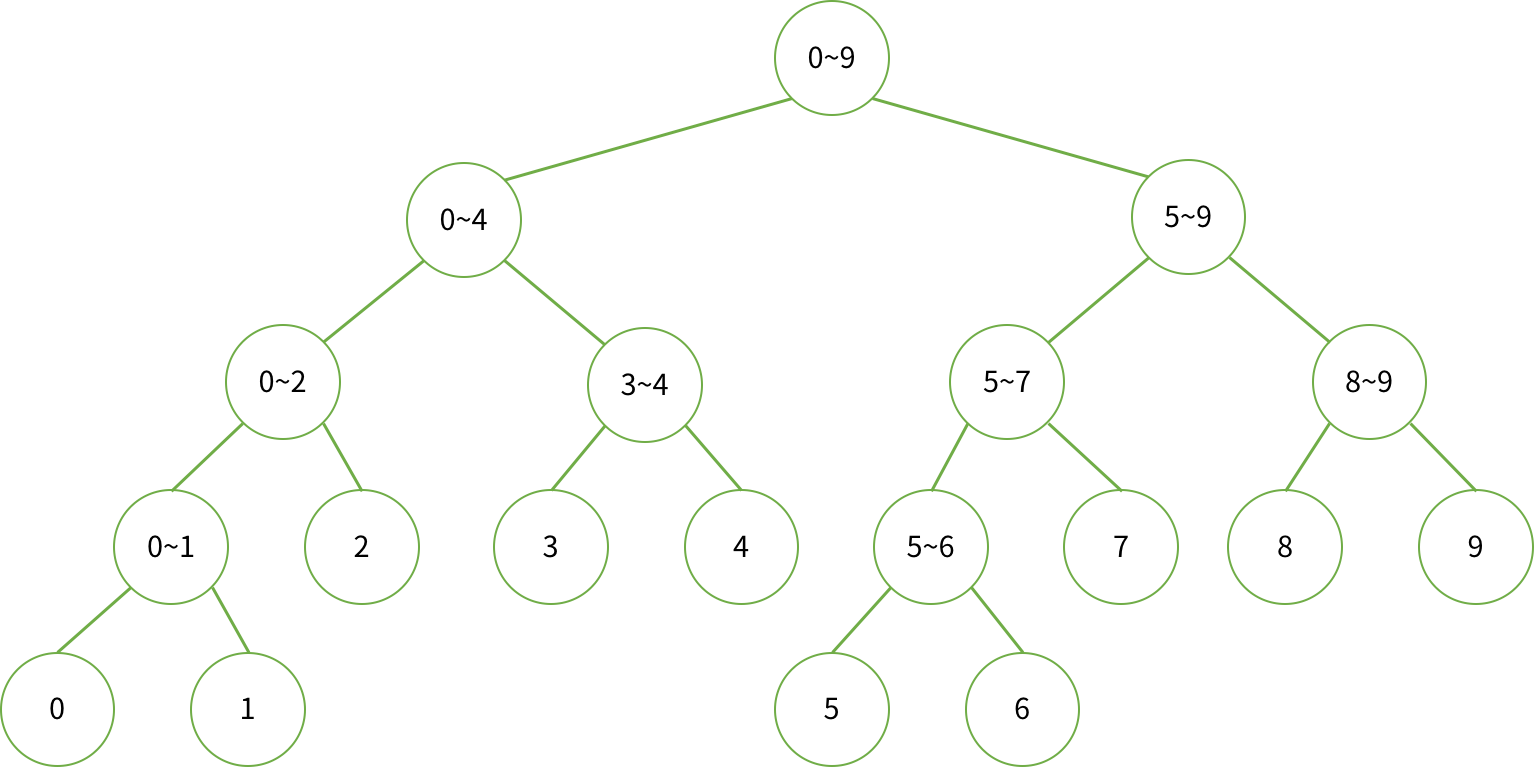각 노드가 저장하고 있는 합의 범위를 나타낸 그림
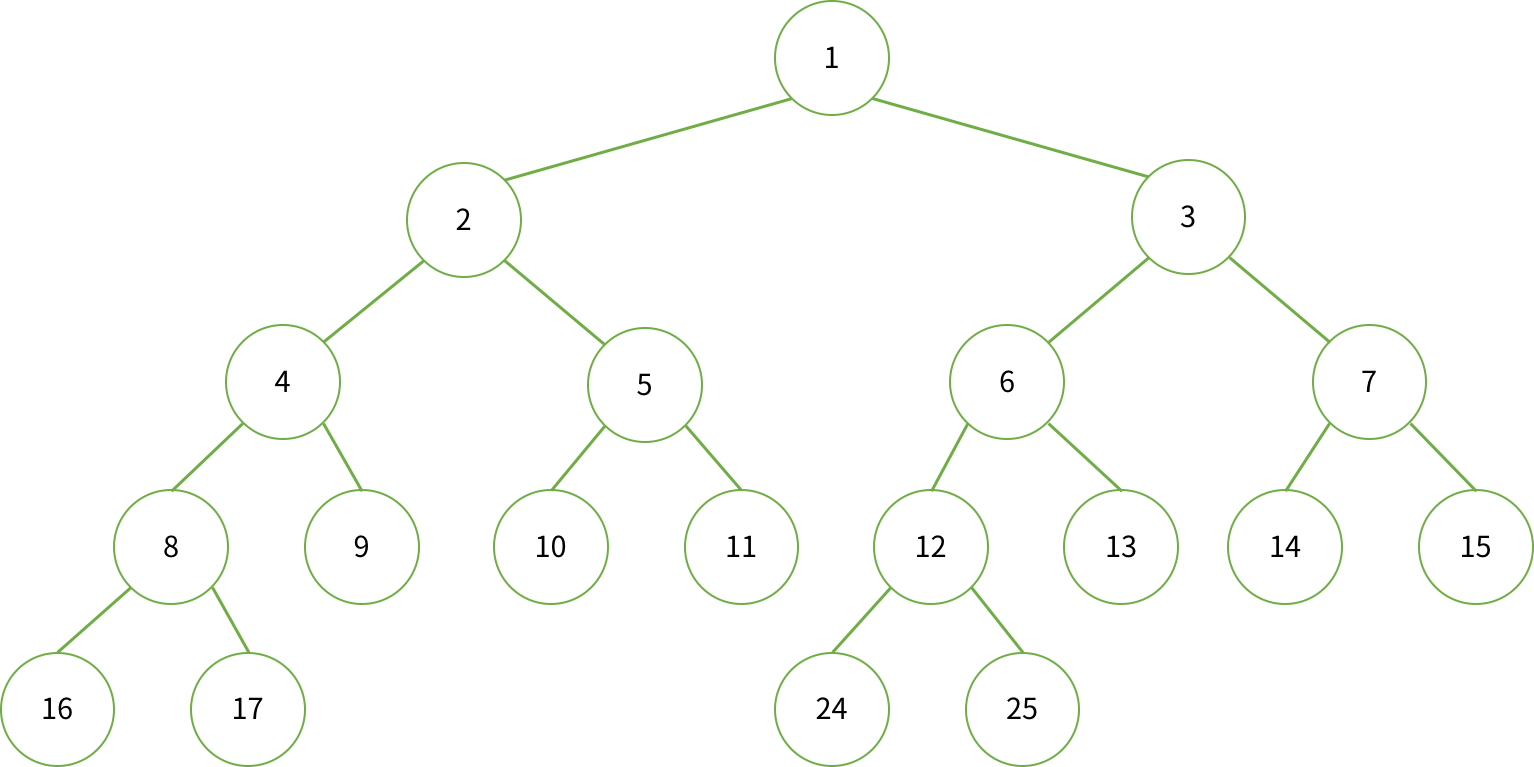각 노드의 index 번호

---

구현

• N이 2의 제곱꼴인 경우, Full Binary Tree이고, 높이는 lgN, 필요한 노드의 개수가 2*N-1개
• N이 2의 제곱꼴이 아닌 경우, 높이는 H= $\lceil$ lgN $\rceil$ 이고, 필요한 노드의 개수는 2^(H+1)-1개

Segment Tree 만들기

// a: 배열 a
// tree: 세그먼트 트리
// node: 세그먼트 트리 노드 번호
// node가 담당하는 합의 범위가 start ~ end
long long init(vector<long long> &a, vector<long long> &tree, int node, int start, int end) {
    if (start == end) {	// Leaf 노드
        return tree[node] = a[start];
    } else {	// 다른 노드
        return tree[node] = init(a, tree, node*2, start, (start+end)/2) + init(a, tree, node*2+1, (start+end)/2+1, end);
    }
}

합 찾기

: 구간 left, right가 주어졌을 때, 합 찾기 위해 루트부터 트리 순회하며 각 노드가 담당하는 구간과 left, right사이의 관계 살펴봐야 한다.

ex) 3~9까지의 합 구하기

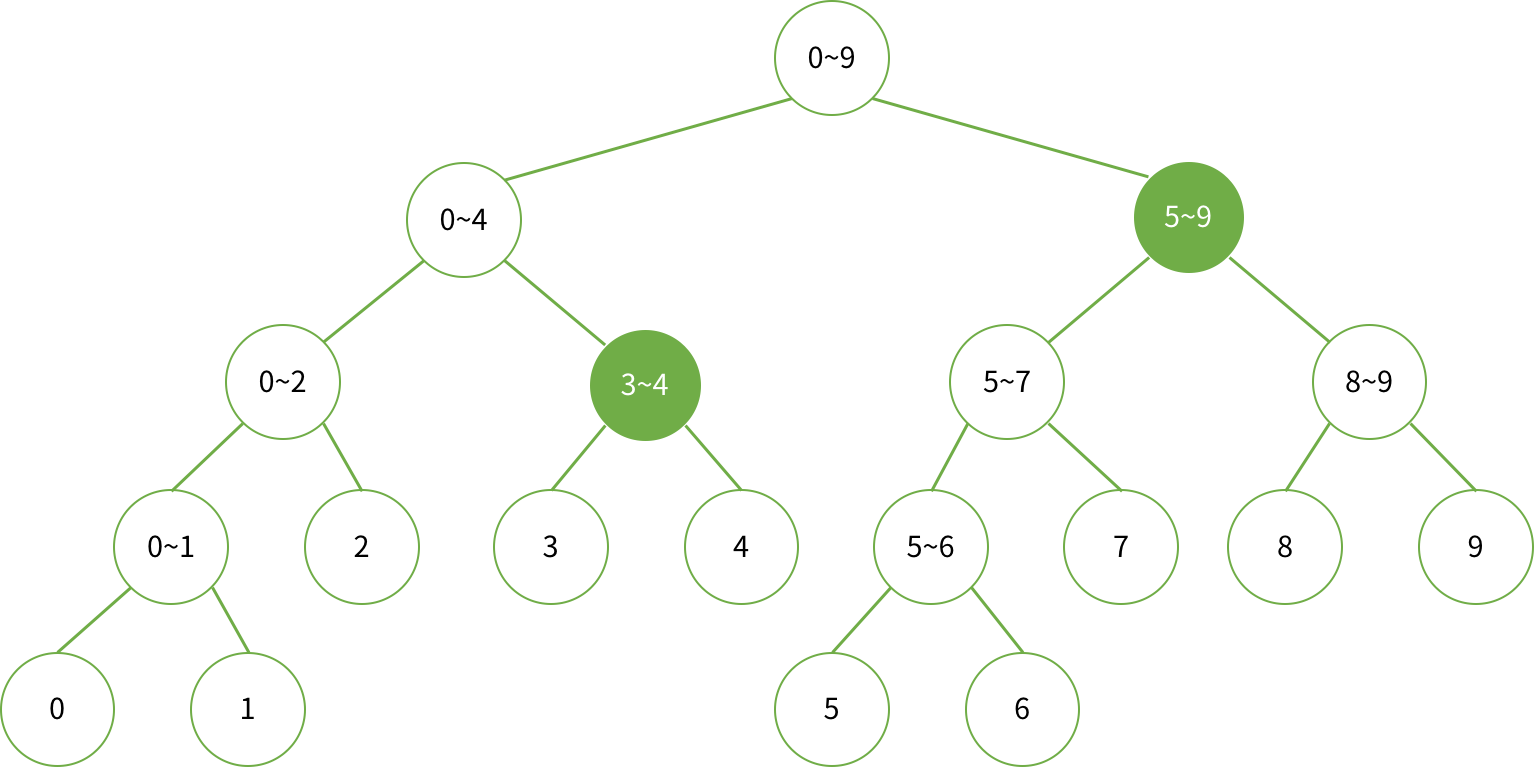
node가 담당하고 있는 구간이 [start,end] 이고, 합을 구해야하는 구간이 [left,right] 이라면 다음과 같이 4가지 경우

1. [left,right]와 [start,end]가 겹치지 않는 경우
2. [left,right]가 [start,end]를 완전히 포함하는 경우
3. [start,end]가 [left,right]를 완전히 포함하는 경우
4. [left,right]와 [start,end]가 겹쳐져 있는 경우 (1, 2, 3 제외한 나머지 경우) → 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색 시작

// node가 담당하는 구간이 start~end이고, 구해야하는 합의 범위는 left~right
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right) {
    if (left > end || right < start) {	// 1번
        return 0;
    }
    if (left <= start && end <= right) {	// 2번
        return tree[node];	
    }
    // 3번 & 4번
    return sum(tree, node*2, start, (start+end)/2, left, right) + sum(tree, node*2+1, (start+end)/2+1, end, left, right);
}

수 변경

: 중간에 수 변경할 경우, 그 숫자가 포함된 구간을 담당하는 노드를 모두 변경해야 한다.

ex) 3번째 수를 변경하는 경우

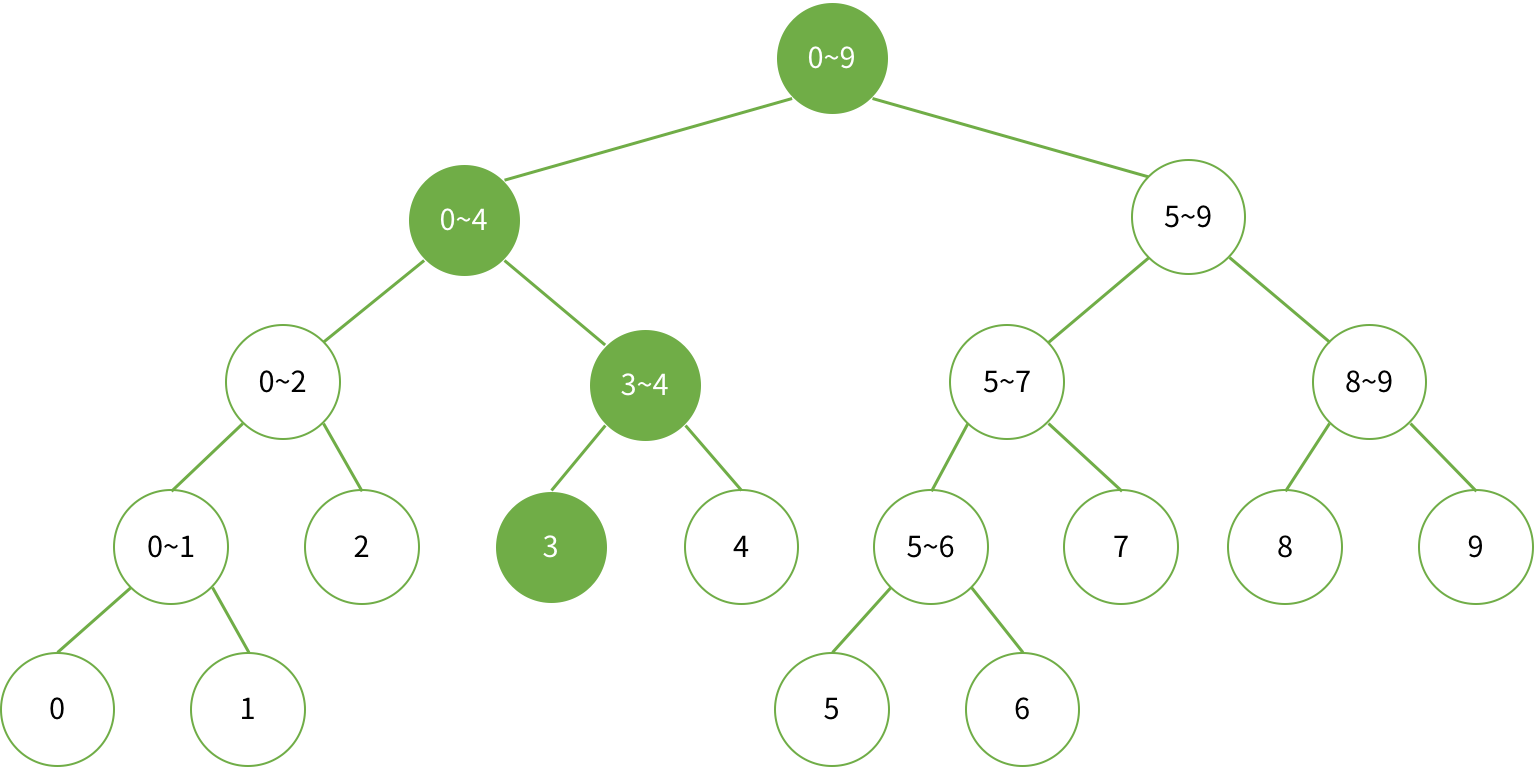
• index 번째 수를 val로 변경한다면, 수가 얼만큼 변했는지(diff) 알아야함-> diff = val - a[index]

수 변경은 2가지 경우

1. [start,end]에 index가 포함되는 경우
2. [start,end]에 index가 포함되지 않는 경우

void update(vector<long long> &tree, int node, int start, int end, int index, long long diff) {
    if (index < start || index > end) return;	// 포함 X
    // 포함 O
    tree[node] = tree[node] + diff;	
    if (start != end) {	// Leaf 노드가 아닌 경우, 자식도 변경
        update(tree,node*2, start, (start+end)/2, index, diff);
        update(tree,node*2+1, (start+end)/2+1, end, index, diff);
    }
}

---

참조 사이트
https://www.acmicpc.net/blog/view/9