📜 문제
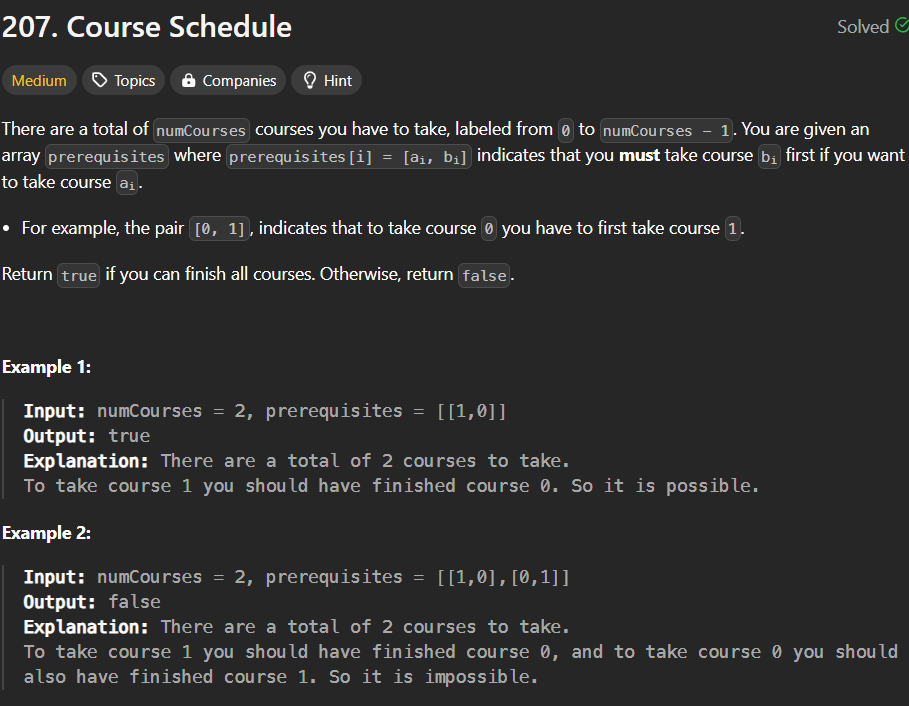
0~numCourse-1까지 모든 과목을 수강할 수 있는지 여부 반환- 선수 과목이 있는 경우, 선수 과목을 먼저 수강해야 함.
생각하기
처음 고민했을 땐 위상정렬이라고는 생각을 못했다.
[0,1], [1,0] 선이수 과목끼리 싸이클이 생기게 되면 모든 과목을 들을 수가 없음을 깨닫고,
싸이클이 생기면 false를 반환하면 되겠다고 생각해서 코드를 쳤다. 근데 걍 틀림
싸이클 여부를 찾은 건 잘했는데, 위상 정렬이랑 안 친해서.. 몰랐어유
그래서 오늘 위상정렬 공부했음
❓ 위상정렬
위상 정렬(Topology Sort)이란?
방향이 있는 비순환 그래프 (DAG, Directed Acyclic Graph)에서 사용
-
작업 i와 작업 j 사이에 간선
(i, j)가 존재한다면 작업 i는 반드시 작업 j보다 먼저 수행되고, 그래프의 모든 간선이 이런 성질을 만족하는 정렬을 의미한다. -
위상 정렬은 사이클이 없는 유향 그래프
G=(V, E)에서 V의 모든 정점을 정렬하되 정렬 결과에서 정점 i는 반드시 정점 j보다 앞에 위치해야한다.
만일 그래프에 사이클이 존재한다면, 해당 성질은 결코 만족될 수 없으므로 위상 정렬은 할 수 없다.
넘 이론적인 얘기라서 이해가 어려울 수 있다.
간단히 대학교 전공 수업처럼 선이수 과목 먼저 수강해야 다음 거 들을 수 있음.
그런데 a의 선이수 과목이 b고 b의 선이수 과목이 a면 말도 안 된다는 의미
위상 정렬 방법
Kahn's Algorithm: 진입차수와 큐를 이용DFS: 그래프를 DFS로 탐색하면서 작업을 스택에 쌓음
문제 풀 때 칸 알고리즘 사용했으니 먼저 소개하겠다.
dfs 풀이는 210. Course Schedule II 문제도 같이 풀어서 아래에 설명
1. Kahn's Algorithm
public static boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] list =new List[numCourses];
List<Integer> res = new ArrayList<>();
int [] indegree = new int[numCourses];
for(int [] pair : prerequisites){
int after =pair[0];
int before = pair[1];
if(list[before]==null){
list[before] = new ArrayList<>();
}
list[before].add(after);
indegree[after]++;
}
Queue<Integer> que = new ArrayDeque<>();
for(int i=0;i<numCourses;i++){
if(indegree[i]==0){
que.offer(i);
}
}
while(!que.isEmpty()){
int cur = que.poll();
res.add(cur);
if(list[cur]!=null){
for(int v: list[cur]){
indegree[v]--;
if(indegree[v]==0){
que.offer(v);
}
}
}
}
System.out.println( res.size() == numCourses);
return res.size() == numCourses;
}✍ 부분 코드 설명
변수 선언 및 초기화
public static boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] list =new List[numCourses];
List<Integer> res = new ArrayList<>();
int [] indegree = new int[numCourses];
for(int [] pair : prerequisites){
int after =pair[0];
int before = pair[1];
if(list[before]==null){
list[before] = new ArrayList<>();
}
list[before].add(after);
indegree[after]++;
}
...list: 정점 별 진출 정점 저장indegree: 정점 별 진입 차수 저장res: 진입 차수가 0인 (방문 가능한) 정점 저장
위상 정렬
...
Queue<Integer> que = new ArrayDeque<>();
for(int i=0;i<numCourses;i++){
if(indegree[i]==0){
que.offer(i);
}
}
while(!que.isEmpty()){
int cur = que.poll();
res.add(cur);
if(list[cur]!=null){
for(int v: list[cur]){
indegree[v]--;
if(indegree[v]==0){
que.offer(v);
}
}
}
}
System.out.println( res.size() == numCourses);
return res.size() == numCourses;
}
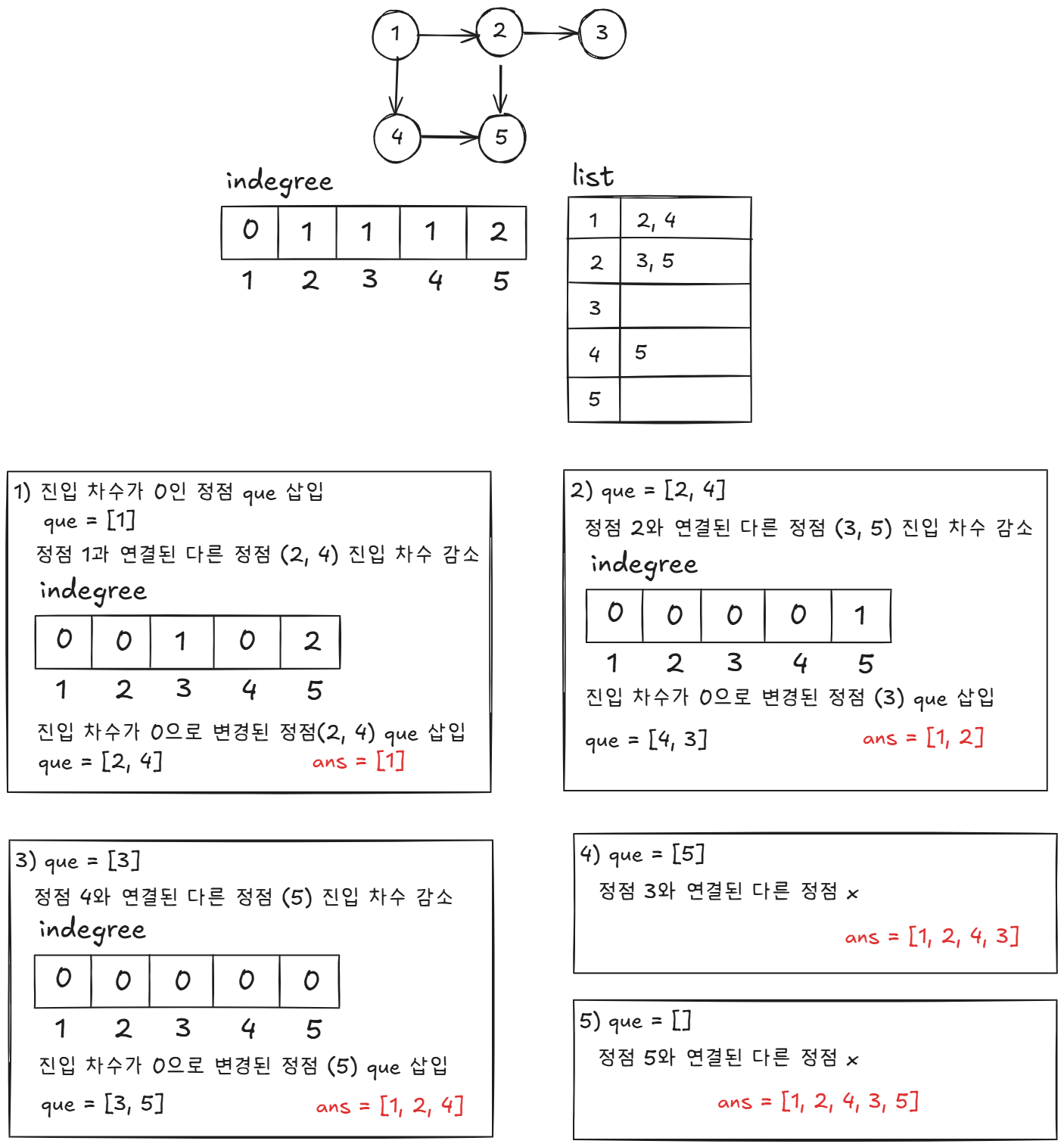
- 진입 차수가 0인 정점 que에 삽입
- 순차적으로 que에서 정점 제거 및 res에 해당 정점 삽입
- 현재 정점 (cur)의 진출 정점이 존재하는 경우, 해당 진출 정점들의 진입 차수 감소.
1 ~ 3과정을 que가 빌 때까지 반복
백문이 불여일견
2. DFS & Stack
package Arrays_Hashing;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class N_210 {
static List<List<Integer>> list;
static Stack<Integer> stack;
static boolean [] visited;
static boolean [] finish;
static boolean cycle;
public static int[]canFinish(int numCourses, int[][] prerequisites) {
list =new ArrayList<>();
stack = new Stack<>();
visited = new boolean[numCourses];
finish = new boolean[numCourses];
cycle =false;
for(int i=0;i<numCourses;i++){
list.add(new ArrayList<>());
}
for(int [] pair: prerequisites){
int after= pair[0];
int before= pair[1];
list.get(before).add(after);
}
for(int i=0;i<numCourses;i++){
if(!visited[i]){
dfs(i);
}
}
int [] res = new int[numCourses];
if(!cycle){
int idx =0;
while(!stack.isEmpty()){
res[idx++] = stack.pop();
}
}
else{
return res;
}
System.out.println(true);
return res;
}
public static void dfs(int cur){
if(cycle){
return;
}
visited[cur] = true;
for(int next : list.get(cur)){
if(!visited[next]) {
dfs(next);
}
else if(!finish[next]){
cycle = true;
return;
}
}
finish[cur]=true;
stack.push(cur);
}
public static void main(String[] args) {
int numCourses = 2;
int [][] prerequisites = new int[][]{
{1,0},
{0,1}
};
canFinish(numCourses, prerequisites);
}
}
✍ 부분 코드 설명
변수 선언 및 초기화
public class N_210 {
static List<List<Integer>> list;
static Stack<Integer> stack;
static boolean [] visited;
static boolean [] finish;
static boolean cycle;
public static int[]canFinish(int numCourses, int[][] prerequisites) {
list =new ArrayList<>();
stack = new Stack<>();
visited = new boolean[numCourses];
finish = new boolean[numCourses];
cycle =false;
for(int i=0;i<numCourses;i++){
list.add(new ArrayList<>());
}
for(int [] pair: prerequisites){
int after= pair[0];
int before= pair[1];
list.get(before).add(after);
}
...list: 정점 별 진출 정점 저장visited: 정점 별 방문 여부finish: 정점 별 방문 완료 여부cycle: cycle 존재 여부
위상 정렬
...
for(int i=0;i<numCourses;i++){
if(!visited[i]){
dfs(i);
}
}
int [] res = new int[numCourses];
if(!cycle){
int idx =0;
while(!stack.isEmpty()){
res[idx++] = stack.pop();
}
}
else{
return res;
}
System.out.println(true);
return res;
}
public static void dfs(int cur){
if(cycle){
return;
}
visited[cur] = true;
for(int next : list.get(cur)){
if(!visited[next]) {
dfs(next);
}
else if(!finish[next]){
cycle = true;
return;
}
}
finish[cur]=true;
stack.push(cur);
}
- 현재 방문하지 않은 정점 기준, dfs 호출
- 현재 정점 방문 처리 & 진출 정점 확인
2-1) 진출 정점에 방문하지 않은 경우 해당 정점 기준 재귀 호출
2-2) 진출 정점에 이미 방문 했지만, 완료된 정점이 아닌 경우, 그래프 내에 싸이클이 존재하므로 탐색 하지 않고RETURN- 더이상 진출 정점이 없는 경우, 방문 완료 처리 및 stack 삽입
이렇게 하면, 방문해야 하는 순서대로 stack에 저장되므로 순서도 파악할 수 있다.
✨ 결과
학부생때 위상 정렬 배웠는데,, 아예 안써서 기억의 저편으로 넘어가버렸다.
그래도 오늘 다시 공부했으니 다행~
내가 접근한 풀이를 보여주자면
static boolean [] visited;
static Map<Integer, List<Integer>> map;
static boolean res;
public static boolean canFinish(int numCourses, int[][] prerequisites) {
res = true;
map =new HashMap<>();
for(int [] pre: prerequisites){
List<Integer> tmp = map.getOrDefault(pre[0], new ArrayList<>());
tmp.add(pre[1]);
map.put(pre[0],tmp);
}
for(int i=0;i<numCourses;i++){
visited = new boolean[numCourses];
if(!visited[i] && map.containsKey(i)){
for(int v : map.get(i)){
dfs(v);
visited[i]=true;
}
}
if(!res){
System.out.println(res);
return false;
}
}
System.out.println(res);
return res;
}
public static void dfs(int cur){
if(map.get(cur)==null){
return;
}
if(!visited[cur]){
visited[cur]=true;
for(int v: map.get(cur)){
dfs(v);
}
if(!res){
return;
}
}else{
res = false;
}
}dfs로 접근헀는데,, 싸이클 체크를 괴상하게 구현해서 틀림 ㅎㅎ