[백준-자바] N_1629 곱셈

0woy·2024년 4월 4일

코딩테스트

목록 보기

14/40

📜 문제

2,147,483,647 이하의 자연수 a, b, c가 주어진다.
a를 b번 곱한 수를 c로 나눈 나머지를 출력한다.

재귀를 이용해 푸는 문제이다.
간단해 보이지만, 메모리 제한과 시간 제한이 심상치 않다.

문제를 읽고 넘 간단해서 엥? 하고 뚝딱뚝딱 코드를 짜고 돌렸는데, 메모리 초과 에러가 발생했다.
2,147,483,647 이하의 자연수는 오버플로우에 걸리기 딱 좋다..

결국 다른 분의 문제 풀이를 보고 수학 공식을 이용해서 풀어야 함을 알았다.

공식

1. 지수 법칙

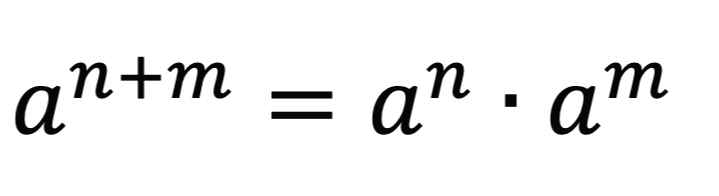
2. 모듈러 연산

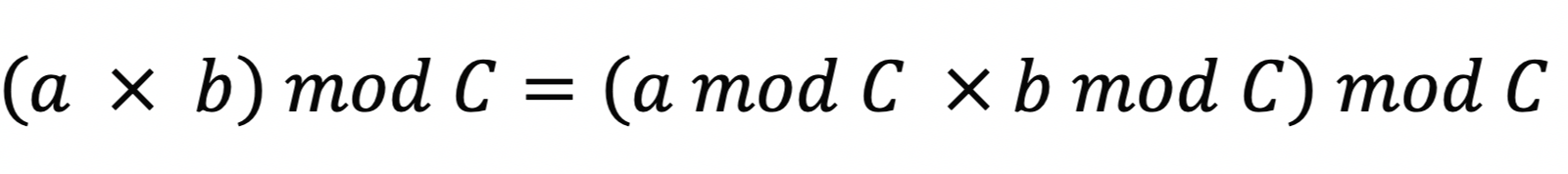
문제 예제인 a=10, b=11, c=12인 경우를 예로 들자.
우리는 10의 11승인 10¹¹을 구해야 한다.

값	지수 법칙
10¹¹	10⁵ * 10⁵ * 10¹
10⁵	10² * 10² * 10¹
10²	10¹ * 10¹

따라서 우리는 10⁵, 10² 만 구하면, 찾아야 하는 10¹¹을 구할 수 있다.

✍ 부분 코드 설명

변수 선언

public static void main(String[] args) throws IOException {
        BufferedReader br = 
		  new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        long n = Long.parseLong(st.nextToken());
        long pow = Long.parseLong(st.nextToken());
        long div = Long.parseLong(st.nextToken());
        ...

n: 곱하는 수 (a)
pow : 곱하는 횟수 (b)
div: 나누는 수

거듭 제곱 구하기

 public static long mul(long n,long pow, long div){
        if(pow==1) return n%div;
        long tmp = mul(n, pow/2, div);
  
  		// 값이 홀수인 경우
        if(pow%2==1) {
            return (tmp*tmp%div)* n%div;
        }
  
  		// 짝수인 경우
        return tmp*tmp %div;
    }

여기서 눈여겨 봐야하는 점은 return문이다.
지수 법칙을 이용한 건 인정하지만 왜 모듈러 연산을 이용해야 할까?
그것은 문제에 주어진 a, b, c는 2,147,483,647 이하의 자연수라는 조건때문이다.

int 자료형의 최대값은 문제에 제기된 2,147,483,647 (2³¹-1)이다.
long 자료형의 최대값은 9,223,372,036,854,775,807 (2⁶³-1) 이다.

tmp 값이 2,147,483,647인 경우, tmp * tmp 값은 long 자료형을 초과하지 않지만, n이 2,147,483,647이라면 말이 달라진다.

pow 값이 홀수인 경우 우리는 tmp * tmp * n 을 수행해야 하는데,
그렇게 되면 long 자료형의 최댓값을 가뿐히 초과한다.

그래서 우리는 모듈러 연산을 수행해서 오버플로우가 발생하지 않도록 하는 것이다.

위에 설명한 모듈러 연산에서 a 값을 tmp * tmp, b 값을 n이라고 칭하면

// 모듈러 연산
(a * b) % c = (a % c * b % c) % c

(tmp * tmp * n) % div 
= ((tmp * tmp % div) * (n % div)) % div

// tmp * tmp % div = (tmp * tmp % div) % div) 와 같다.
= (((tmp * tmp % div) % div) * (n % div)) % div

// 모듈러 연산: (tmp * tmp % div) % div를 한 이유
= ((tmp * tmp % div) * n ) % div

모듈러 연산을 사용하면, pow가 홀수인 경우 오버플로우가 발생하지 않는다.

🍳 전체 소스 코드

package Algorithm.Recursion;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class N_1629 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        long n = Long.parseLong(st.nextToken());
        long pow = Long.parseLong(st.nextToken());
        long div = Long.parseLong(st.nextToken());
        System.out.println(mul(n,pow,div));

    }

    public static long mul(long n,long pow, long div){
        if(pow==1) return n%div;
        long tmp = mul(n, pow/2, div);
        if(pow%2==1) {
            return (tmp*tmp%div)* n%div;
        }
        return tmp*tmp %div;
    }

}