📜 문제
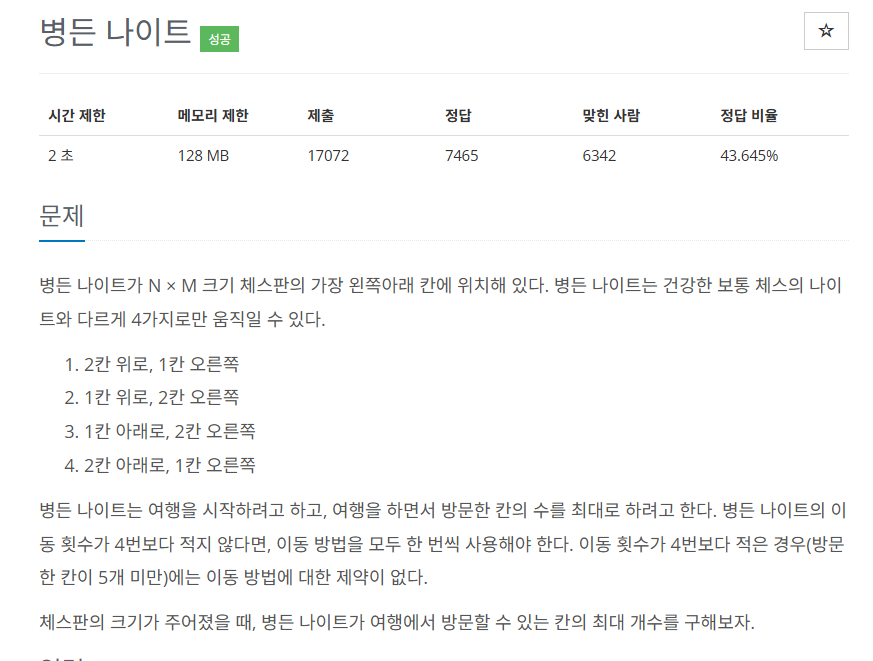
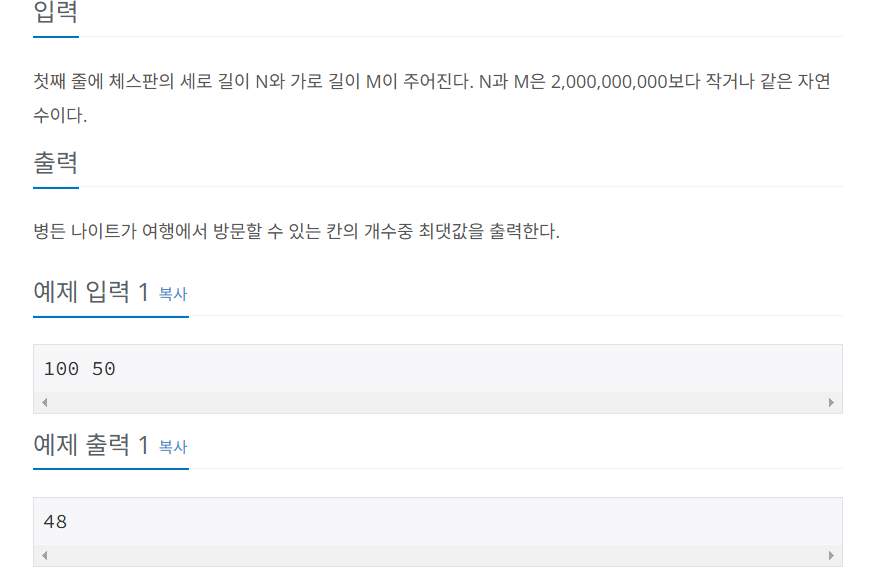
- NxM 크기의 체스 보드
- 나이트의 시작 위치: (N,1)
0이 아닌 1부터 시작한다고 가정 - 이동할 수 있는 칸의 최대 개수 구하기
이때, 최대 개수가 5이상인 경우, 모든 방법을 한 번 이상 사용해야함.
생각하기
만일, 모든 방법을 다 쓴다고 가정할 때, 최소 배열의 크기를 생각해 보자.
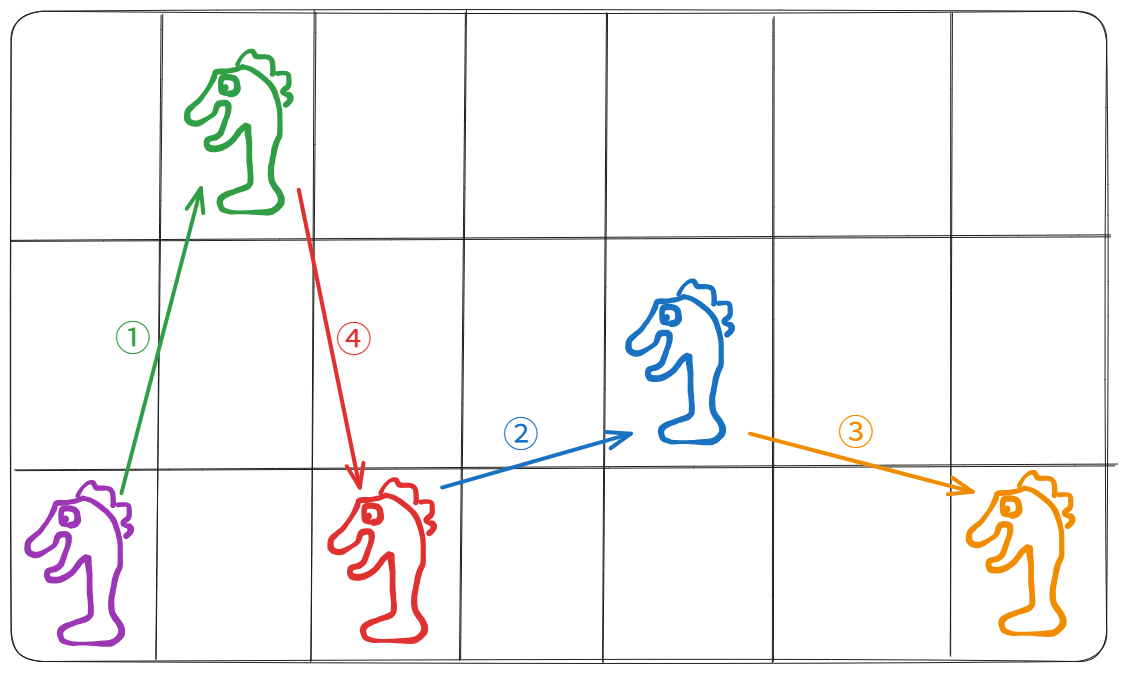
위 그림에서 보듯, 최소 세로(N)≥3, 가로(M)≥7 인 경우 4가지 방법을 모두 사용할 수 있다.
1. N =2
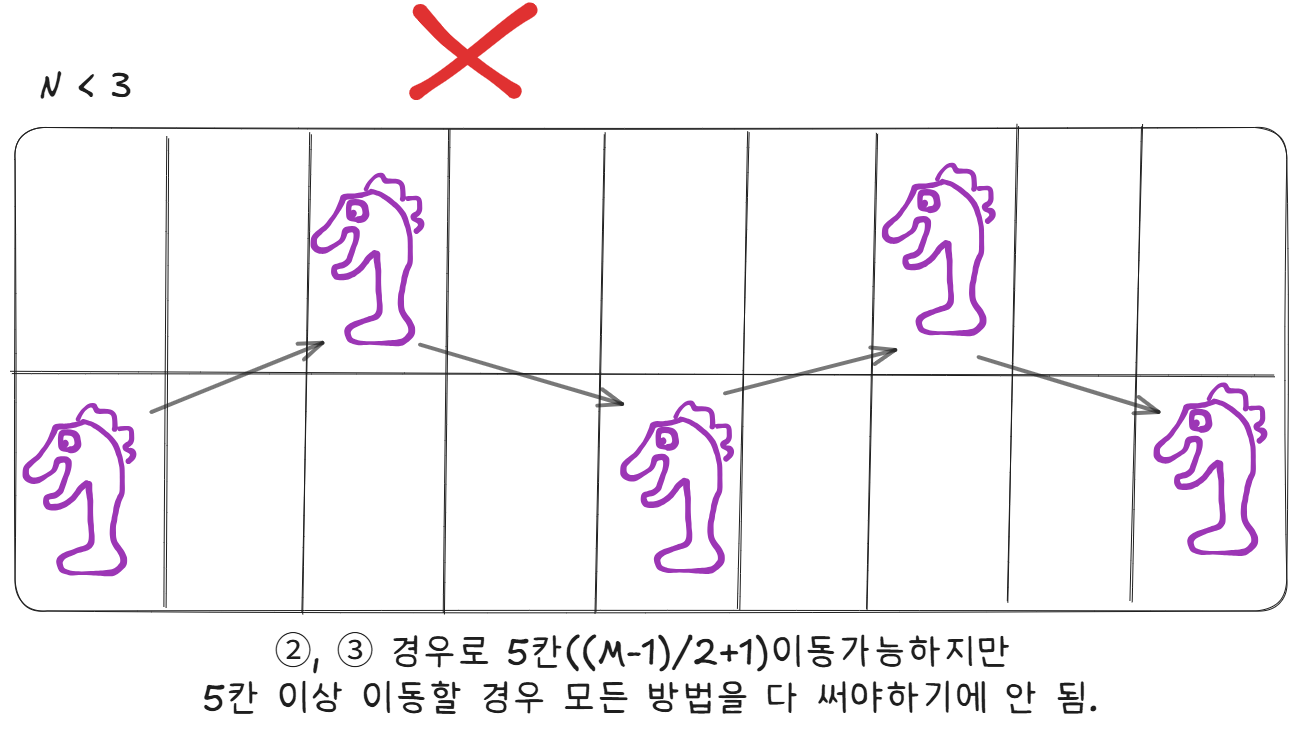
세로가 2인 경우, ①, ④ 방법은 쓸 수 없다. (왜 ??? 체스판을 벗어나니까.)
따라서 아무리 이동을 많이 할 수 있어도 문제 조건을 충족할 수 없기 때문에 이동 가능한 칸 수는 최대 4칸이다.
시작 칸을 제외하면 가로 길이는 M-1이 된다.
②, ③ 방법을 쓰면, 2칸씩 이동하므로 이동 가능한 칸 수 = (M-1)/2
시작 위치도 포함해야 하기 때문에 +1을 더한다.∴ 최대 이동 칸 = Math.min(4, (M-1)/2 + 1)
2. M < 7
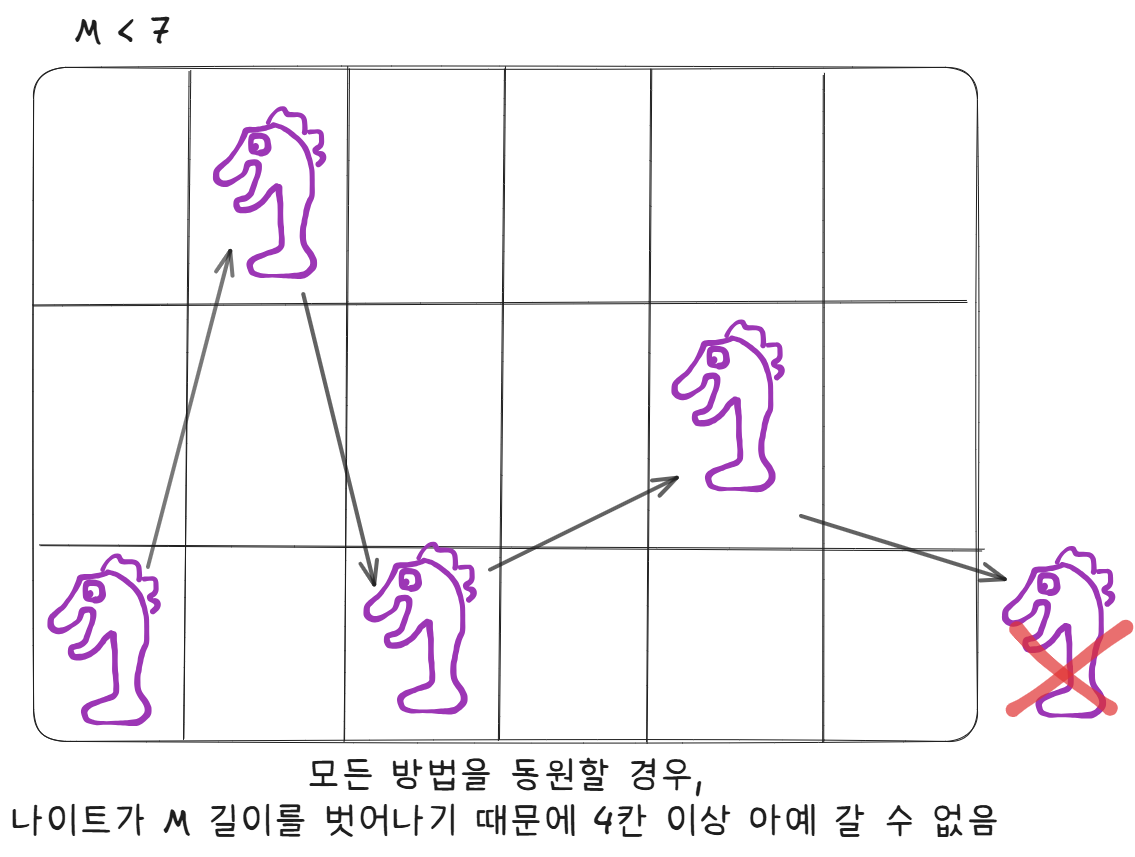
나이트가 이동할 수 있는 방법은 모두 우측으로 +1칸 혹은 +2칸씩 이동한다.
그래서 시작 위치를 제외하고 최소 1+1+2+2 = 6칸이 있어야 4가지 방법을 모두 사용할 수 있다.
4칸 이하는 특정 방법만 사용해도 되므로, ①, ④ 방법만 취하면 된다.
∴ 최대 이동 칸 = Math.min(4, M)
3. N≥3, M≥7
4가지 방법을 사용할 수 있는 체스판의 최소 크기를 충족한 경우에는 어떨까?
우측으로 +2 이동하는 방법은 1번 씩만 써서 2칸을 이동하고, 나머지를 우측으로 +1만 이동하면 된다.
- ②, ③ 방법을 사용 시 남은 가로 길이: M-4(2+2)
- ①, ④ 방법으로 나머지
M-4길이 이동∴ 최대 이동 칸 = 2+M-4 = M-2
🍳 전체 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class N_1783 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int count =0;
if(N==1){
count=1;
}else if(N==2){
count = Math.min(4, (M-1)/2+1);
}else if(M<7){
count = Math.min(4,M);
}else{
count = M-2;
}
System.out.println(count);
}
}
✨ 결과
문제도 이해 못해서 빠르게 답을 봤다.
답을 보니 머리가 똑똑해진 기분 세상엔 영리한 사람들이 참 많다!
나도 그렇게 될 거지롱

