Amdahl's law 이해하기

0xf4d3c0d3·2022년 3월 22일

개요

얼마전에 다른 글을 정리하다 Amdahl's law에 대해 정리할 필요가 있었다.

this law models system scalability, accounting for serial components of workloads that do not scale in parallel. It can be used to study the scaling of CPUs, threads, workloads, and more

원문은 이러했는데 정확히 무슨 뜻인지 이해가 잘 되지 않아 위키를 찾아봤다. 위키피디아도 그렇고 나무위키도 그렇고 정의는 간단했다. 컴퓨터 시스템의 일부를 개선할 때 전체적으로 얼마만큼의 최대 성능 향상이 있는지 계산하는 데 사용된다 라는데 여전히 원문의 "serial components", "that do not scale in parallel"이 신경 쓰여 더 자세히 알아보고자 영문판 위키피디아를 보니 자료가 꽤 많이 나왔는다. 이에 대해 정리해보면 좋을것 같다.

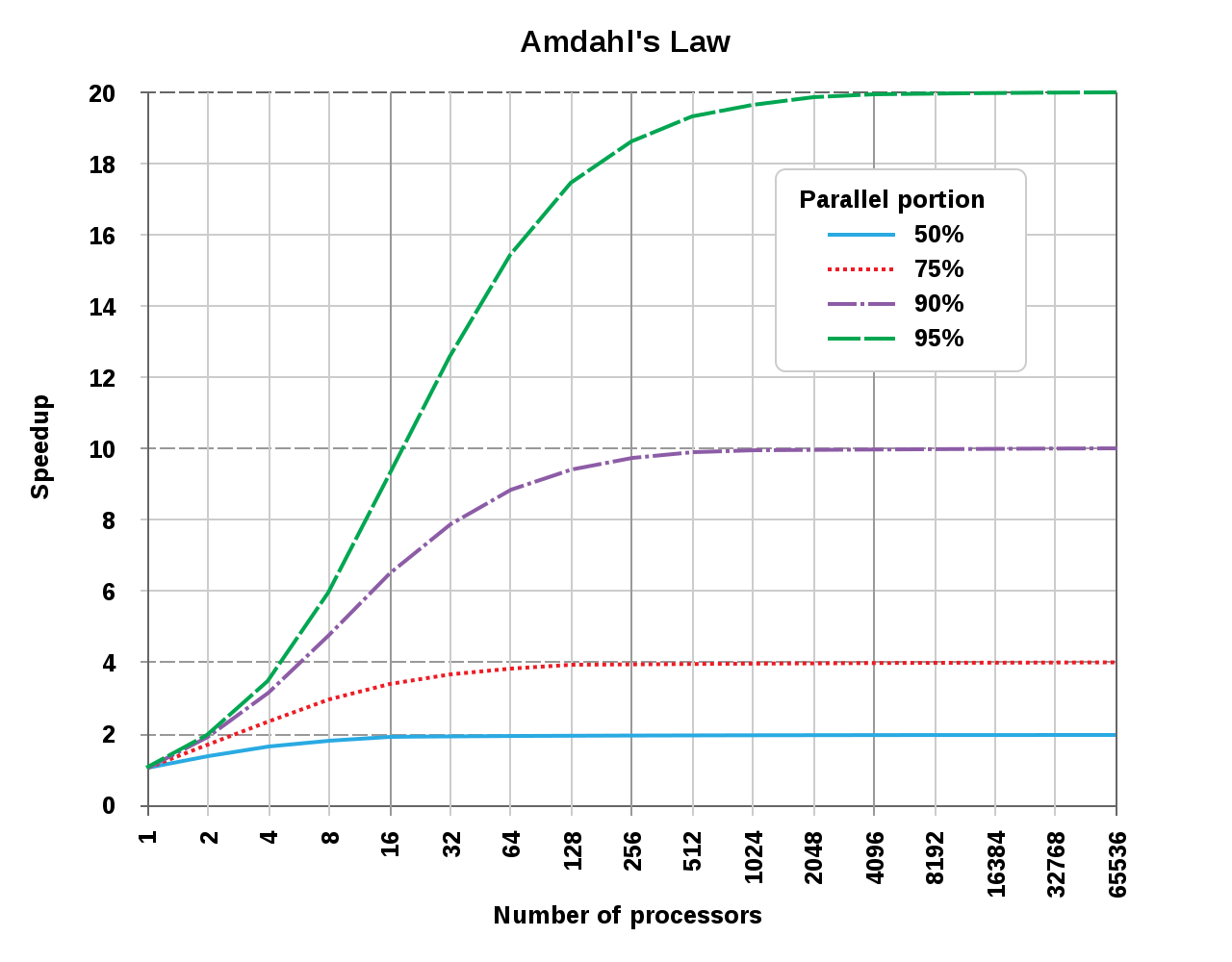
예시를 먼저 보고 가자. 싱글쓰레드에서 20시간 걸리는 작업이 있는데 이중 1시간은 병렬로 처리할 수 없는 구간이 있다고 하면, 오직 19시간(p=0.95)만 병렬 처리가 가능하다. 그럼 얼마나 많은 쓰레드를 사용해 병렬 처리를 하든, 실행 시간은 1시간 이상이 될 것이다. 따라서 이론적인 속도향상은 싱글쓰레드일때의 20배가 최대가 된다. ( $\frac{1}{1-p} = 20$ )

정의

Amdahl's law는 다음과 같이 수식으로 정리될 수 있다:

S_{latency}(s) = \frac{1}{(1-p) + \frac{p}{s}}

$S_{latency}$ : 전체 수행 속도가 이론적으로 몇배 빨라지는지
$s$ : 해당 파트가 몇배 빨라졌는지
$p$ : 해당 파트가 기존 수행시간에서 몇 퍼센트 비율을 차지하고 있었는지

나아가 다음과 같은 수식들을 도출할 수 있다:

\begin{cases} \displaystyle S_{latency}(s) \le \frac{1}{1-p} \\ \displaystyle\lim_{s\rarr\infin}{S_{latency}(s)} = \frac{1}{1-p} \end{cases}

정의만 보면 "병렬"이란 키워드는 딱히 보이지 않는다. 암달의 법칙을 찾으면 여기저기 보이는 병렬 이란 단어는 속도 개선의 예로 병렬 컴퓨팅을 들었기 때문으로 보인다.

응용

임의의 작업은, 시스템이 개선되었을 때 두 부분으로 나뉠 수 있다:

해당 개선의 효과를 받지 못하는 부분
해당 개선의 효과를 받는 부분

예로, 프로그램이 파일을 처리할때, 프로그램의 일부는 디스크에서 디렉토리를 스캔한 뒤 파일 목록을 메모리에 생성하고 다른 일부는 각 파일들을 각 쓰레드에 넘긴다. 디렉토리를 스캔하고 파일 목록을 생성하는 부분은 병렬로 처리할 수 없지만, 파일을 처리하는 부분은 그럴 수 있다.

개선전의 시스템에서 전체 작업을 수행하는데 걸린 시간을 $T$ 라 하자. 이는 개선 효과를 받지 못하는 부분에서 걸린 시간과 개선 효과를 받는 부분에서 걸린 시간을 모두 포함한다. 개선 효과를 받는 부분이 전체 수행 시간에서 차지 하는 비율을 $p$ 라 하면, 그렇지 않은 부분이 차지하는 비율은 $1-p$ 가 된다.
즉, $T = (1-p)T + pT$

개선 효과를 받는 부분이 $s$ 배 만큼 빨라졌다고 하면 $T(s) = (1-p)T + \frac{p}{s}T$ 라 할 수 있다. Amdahl's law는 부하 $W$ 가 고정되었을때를 다루므로 아래 식으로 정리할 수 있다:

S_{latency}(s) = \frac{TW}{T(s)W} = \frac{T}{T(s)} = \frac{(1-p)T + pT}{(1-p)T + \frac{p}{s}T} = \frac{1}{1-p+\frac{p}{s}}

개선 효과를 받는 부분이 여러개라 해보자. 쉽게 2개일때를 가정해 각각 $p_1$ , $s_1$ , $p_2$ , $s_2$ 라 하겠다.

T = (1-(p_1+p_2))T + p_1T + p_2T

각 부분이 $s_1$ , $s_2$ 배 만큼 속도가 개선되었을 때를 $T(s_1, s_2)$ 라 하면,

T(s_1, s_2) = (1-(p_1+p_2))T + \frac{p_1}{s_1}T + \frac{p_2}{s_2}T

S_{latency}(s) = \frac{T}{T(s_1, s_2)} = \frac{1}{(1-p_1-p_2)+\frac{p_1}{s_1}+\frac{p_2}{s_2}}

개선 효과를 받는 부분이 3개 4개가 되더라도 그 모양은 대충 감이 올것이다.

기본 예시 1

만약 전체 수행 시간의 30% 정도의 속도를 개선할 수 있다고 하면, $p$ 는 0.3이 된다. 그리고 해당 부분의 성능을 2배 개선시킨다 하면, $s$ 는 2가 된다. 따라서 이론적으로 얻을 수 있는 전체 속도 개선은 $\frac{1}{1-0.3+\frac{0.3}{2}} = 1.18$ 배
즉 $1-(\frac{1}{1.18}) = 15$ % 정도다.

이제 작업을 4개 파트로 나누어 수행한다고 해보자. 각 파트가 전체 수행시간에서 차지하는 비율은 p1=0.11, p2=0.18, p3=0.23, p4=0.48 이다. 그리고 각 파트별 속도 개선은 s1=1, s2=5, s3=20, s4=1.6 이다. 이를 위에서 정리한 식으로 계산해보면

S_{latency}(s) = \frac{T}{T(s_1, s_2)} = \frac{1}{(1-p_1-p_2-p_3-p_4)+\frac{p_1}{s_1}+\frac{p_2}{s_2}+\frac{p_3}{s_3}+\frac{p_4}{s_4}} \\

= \frac{1}{\frac{0.11}{1} + \frac{0.18}{5} + \frac{0.23}{20} + \frac{0.48}{1.6}} = 2.19

보다시피, 두번째 세번째 파트가 5배 20배 속도가 개선되었음에도 전체 수행시간의 속도 개선은 크게 영향받지 않았고 전체 수행시간의 48%를 차지하던 네번째 파트의 영향을 크게 받았다.

기본 예시 2

$T_A=3s; T_B=1s$ 인 A와 B 두 부분으로 나뉜 직렬프로그램이 있다고 하자. $p_A=0.25; p_B=0.75$ 로 A에서 속도를 2배 개선시키면 전체 시간은 1.6배 빨라지는 반면, B에선 고생고생하고 속도를 5배나 개선시켜도 전체 시간은 1.25배만 빨라지게 된다.

병렬 프로그램의 직렬 부분 개선 예시 1

병렬처리 하지 못하는 부분을 $O$ 배 만큼 개선했다면,

T(O, s) = (1-p)\frac{T}{O} + \frac{p}{s}T

Amdahl's law에 따라, $p$ 에 해당하는 부분을 $s$ 만큼 개선시켰다면,

S_{latency}(O, s) = \frac{T(O)}{T(O, s)} = \frac{(1-p)\frac{T}{O} + pT}{(1-p)\frac{T}{O} + \frac{p}{s}T}

= \frac{\frac{1-p}{O} + p}{\frac{1-p}{O} + \frac{p}{s}}

$s$ 가 $\infin$ 이면, $S_{latency}(O, s) = 1+\frac{pO}{1-p}$ 가 된다.

즉 병렬로 처리할 수 있는 비율이 $p$ 고 병렬로 처리하지 못하는 부분의 수행시간을 $O$ 배 만큼 줄였다면,
최대로 얻을 수 있는 속도 개선은

1+\frac{pO}{1-p}\quad배

또는

\frac{pO}{1-p+pO}\quad\%

예를 들면 아래와 같다.

a = 70
b = 30

p = b/(a+b)
O = 3
s = 9e9

T_O = a/O + b     # 53.33
T_Os = a/O + b/s  # 23.33

gain = 1+(p*O)/(1-p)  # 2.28
T_O / gain            # 23.33 == T_Os

병렬 프로그램의 직렬 부분 개선 예시 2

병렬 처리하지 못하던 부분을 $O'$ 배 만큼 줄이고 병렬 처리하는 부분을 그만큼 늘렸다고 하자. 그럼,

T'(O', s) = \frac{1-p}{O'}T + (1 - \frac{1-p}{O'})\frac{T}{s}

라 할 수 있다.

이를 함수 S로 정리하면,

S'_{latency}(O', s) = \frac{1}{\frac{1-p}{O'} + (1-\frac{1-p}{O'})\frac{1}{s}}

$s$ 가 $\infin$ 이면, $S'_{latency}(O', s) = \frac{O'}{1-p}$ 가 된다.

즉 병렬로 처리할 수 있는 비율이 $p$ 고 병렬로 처리하지 못하는 부분의 비율을 $O'$ 배 만큼 줄였다면,
최대로 얻을 수 있는 속도 개선은

\frac{O'}{1-p}\quad배

또는

\frac{O'-1+p}{O'}\quad\%

예를 들면 아래와 같다

a = 60
b = 40
T = a + b

p = b/(a+b)
O = 7
s = 9e9

T_O = (1-p)/O * T + (1 - (1-p)/O) * T     # 100 (a와 b의 비율만 바뀌고 개선은 된게 없으므로)
T_Os = (1-p)/O * T + (1 - (1-p)/O) * T/s  # 8.57

gain = O / (1-p)
T_O / gain  # 8.57 == T_Os

실습

CC BY-SA 3.0 AmdahlsLaw.svg

Amdahl's Law를 찾아보면 자주 나오는 그래프다. 한번 직접 그래프를 그려보자.

package main

import (
	"fmt"
	"sync"
	"time"
)

func benchmark(portion float64, proc int) (elapsedTime float64) {
	// 0. 걸린 시간을 float64로 반환
	start := time.Now()
	defer func() {
		elapsedTime = float64(time.Since(start))
	}()

	// 1. 처리해야 할 작업을 총 10000개로 잡고 {portion}%에 해당하는 만큼 병렬로 처리할 수 있게 한다.
    // 나머지는 직렬로 처리하도록 한다.
	const workloadSize = 10000
	workloadParallelSize := int(workloadSize * portion)
	workloadSerialSize := workloadSize - workloadParallelSize

	// 개당 처리 소요 시간
	processingTime := time.Microsecond * 10

	// 2. 병렬로 처리할 작업은 미리 채널에 추가
	workloads := make(chan int, workloadParallelSize)
	for i := 0; i < workloadParallelSize; i++ {
		workloads <- i
	}

	// 3. {proc} 개수만큼 goroutine을 만들어서 병렬로 workload를 처리
	var wg sync.WaitGrou
	wg.Add(proc)
	for i := 0; i < proc; i++ {
		go func() {
			defer wg.Done()

			for {
				select {
				case <-workloads:
					time.Sleep(processingTime)
				default:
					return
				}
			}
		}()
	}
	wg.Wait()

	// 4. 병렬로 처리하지 못하는 부분은 직렬로 처리
	time.Sleep(processingTime * time.Duration(workloadSerialSize))

	return
}

func main() {
	// 0. 기준이 되는 base는 싱글쓰레드에서 100% 직렬처리
	base := benchmark(0.00, 1)
       
    // 1. 각 proportion에서 1~4096개의 고루틴을 돌렸을때 각 차원별로 base 대비 몇배의 속도 개선이 있었는지 기록
	result := make(map[float64][]float64)
	for _, portion := range []float64{0.5, 0.75, 0.90, 0.95} {
		for i := 1; i <= 4096; i++ {
			result[portion] = append(result[portion], base/benchmark(portion, i))
		}
	}


	// 결과를 python dict형태로 출력
	fmt.Printf("{")
	for k, v := range result {
		fmt.Printf("\"%.2f\": [", k)
		for _, w := range v {
			fmt.Printf("%.2f, ", w)
		}
		fmt.Printf("], ")
	}
	fmt.Println("}")

}

아직 golang이 익숙치 않아 몇군데 아쉬운 부분이 있다. 특히 string manipulation 부분은 이게 최선인지 모르겠다. 뭔가 map function 같은게 있었다면 마지막 부분은 strings.Join(map(string, result), ", ") 처럼 할 수 있었을텐데.. 그건 그렇고 위 결과를 그래프로 그려보면 아래와 같다.
변동이 너무 심해 window size를 128로 잡고 이동평균을 취했다.

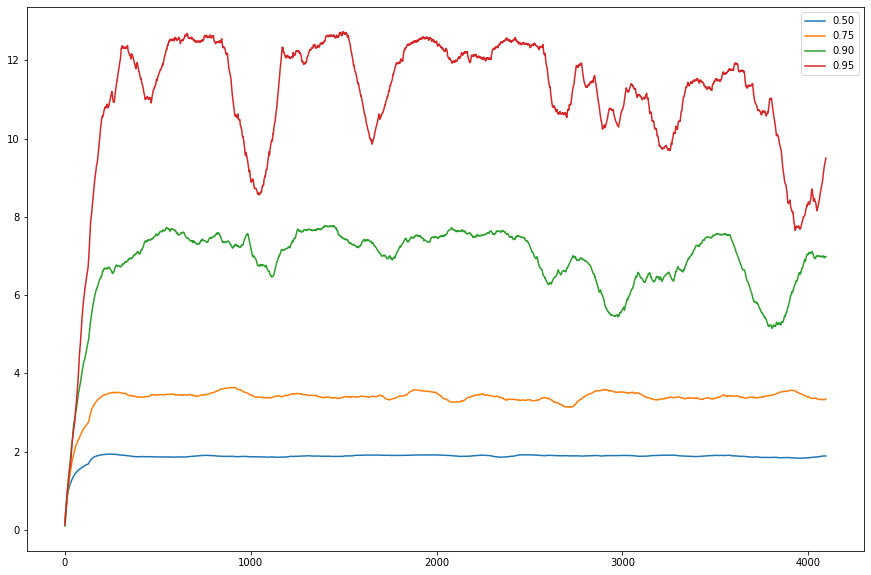
그래프가 이쁘지 않다.. 사실 몇가지 매개변수들을 조절하기 이전의 실험에서는 아래와 같았다.

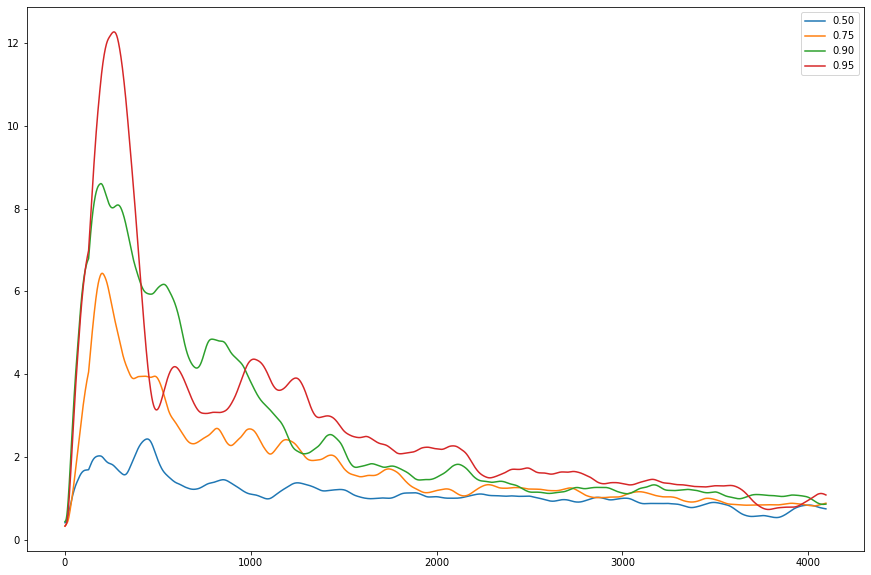
위와 같은 모양이 나오는 이유는 어쩌면

workloadSize가 너무 작으면 proc 갯수가 커져도 효과를 제대로 보지 못해서
processingTime이 너무 작으면 임계영역을 관리하는 비용이 병렬 처리로 볼 수 있는 이득보다 커져서
실제 프로세서 갯수가 느는건 아니므로, concurrency만 늘지 parallelism이 느는건 아니라서
x축이 로그스케일이 아니라서

이지 않을까 싶어 workloadSize는 1000으로 줄이는대신, proc 범위를 1~512로 낮추고, processingTime을 10μs에서 1ms로 크게 늘려 다시 테스트 해봤다. proc 갯수는 그래프처럼 실제 프로세서 갯수로 하기엔 테스트 환경이 8코어라 그러기 어려웠다. 그럼에도 불구하고 결과는 나쁘지 않았다.

변동도 크지 않아 이동평균은 따로 안했고, x축도 2를 밑으로 하는 로그 스케일로 바꿔 그려봤다.

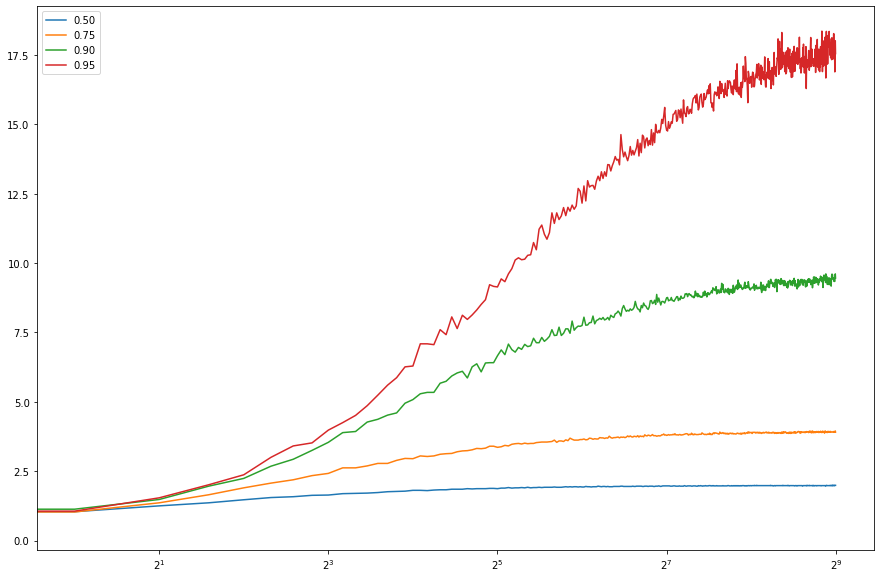
이론적으로 각 proportion에서 얻을 수 있는 속도 개선은 0.90에서 1/(0.1 + 0.9/512) = 9.8, 0.95에서 19.3 으로, 대충 예상한 대로 나와 좋다.

글을 다 쓰고 처음 질문으로 돌아와 "병렬" 이란 단어가 보였던 이유는, contention이나 coherency에 의한 비용을 고려하지 않는다면, "병렬로 처리할 수 있는 부분"을 s배 만큼 할당 하는것이 곧 해당 부분의 속도를 s배만큼 개선하는 것으로 이어지기 때문이 아닌가 싶다.

병렬 프로그램의 직렬 부분 개선 파트를 보면 병렬처리로 s배 만큼 개선할 수 있는 부분 p와 그렇지 못한 부분 1-p가 있을때 이 p와 s가 암달의 법칙에서 어떤 역할을 하는지 이해하기 좀 더 쉬울 것이다.

0xf4d3c0d3

jdh

이전 포스트

Go 1.18 Changes - Workspace

다음 포스트