문제사항
골드 5단계 문제였다.
트리 문제에서 그래프로 푸는 Tree 문제이고, DFS(깊이 우선 탐색)로 풀어야 하는 유형이다.
문제에서 원하는건 트리에서 특정 노드를 제거하였을 때 리프노드의 개수를 출력하면 된다.
문제에 대해 설명하기 전에 리프노드와 같은 트리 관련 구성요소와 트리문제는 어떻게 접근해야되는지 부터 알아보자.
트리 알아보기
트리는 노드와 에지로 연결된 그래프의 특수한 형태 = 그래프의 표현으로도 tree를 표현할 수 있다.
특징
- 순환 구조 X, 필수로 1개의 루트 노드 존재
- 루트 노드 제외한 노드는 단 1개의 부모 노드 가진다.
- 트리의 부분 트리 역시 트리의 모든 특징을 따른다.
⇒ 트리에서 임의의 두 노드를 이어주는 경로는 유일하다.
트리의 핵심 이론
- 트리의 구성 요소
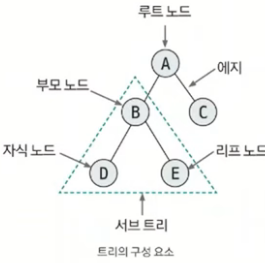

문제에서 말한 리프 노드는 표에서 말하듯 트리에서 가장 하위에 존재하는 노드이다.
Tip) 코딩테스트에서 Tree
(1) 그래프로 푸는 Tree
- Node Edge : 인접리스트로 표현 ⇒ “DFS”, “BFS”(2) Tree만을 위한 문제
- 이진 트리 (난이도 : 중)
- 세그먼트 트리 (index tree) (난이도 : 상)
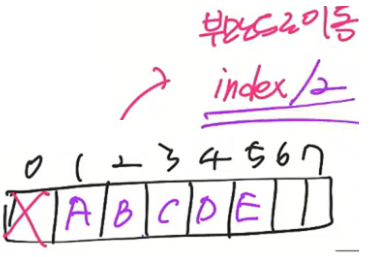
- LCA (최소공통조상) (난이도 : 상)세그먼트 트리 : 1차원 배열로 tree 표현
ex) 5/2 = 2 : E의 부모는 B
3/2 = 1 : C의 부모는 A자식으로 이동할 때는 index x 2 혹은 index x 2 +1
다시 한번 말하자면 위 문제는 트리에서 노드를 하나 제거한 후 남은 리프 노드의 개수를 구하는 문제이다. DFS(깊이 우선 탐색)를 사용하여 효율적으로 해결할 수 있다.
알고리즘 분류
트리, DFS
코드
두 가지 방법으로 푸었다.
먼저 첫 번째 풀이의 특징을 살펴보자.
-
부모에서 자식으로의 단방향 그래프를 사용하였다.
-
그래프에서 삭제할 노드를 직접 제거하였다. (루트가 삭제 대상일 경우 DFS 수행 X)
-
리프 노드 수를 자식에서 부모로 누적하여 계산하였다.
-
각 노드의 서브트리에 있는 리프 노드 수를 배열에 저장하였다.
첫 번째 방법은 트리의 구조에 초점을 맞춰 풀었기 때문에 일반적인 그래프 탐색과 거리가 멀다.
코드 1
import java.io.*;
import java.util.*;
public class Main {
static ArrayList<Integer>[] graph;
static int[] leaf;
static int N, target, root; // N: 노드 개수, target: 삭제할 노드, root: 루트 노드
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine()); //N은 50보다 작거나 같은 자연수
leaf = new int[N];
graph = new ArrayList[N + 1]; //인접리스트 초기화 (리스트의 배열(또는 리스트의 리스트))
for (int i = 0; i < N; i++) {
graph[i] = new ArrayList<>();
}
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent == -1) {
root = i;
} else {
graph[parent].add(i); // 부모 노드에 자식 노드 추가
}
}
target = Integer.parseInt(br.readLine()); //지울 노드의 번호
for (int i = 0; i < N; i++) {
graph[i].removeIf(integer -> integer == target); // 삭제할 노드를 자식으로 가진 노드에서 제거
//그래프 속 지울 노드의 번호 삭제
}
if(target != root) DFS(root, -1);// 루트가 삭제 대상이 아닐 경우에만 DFS 수행
System.out.println(leaf[root]);
}
static void DFS(int v, int parent) {
if(graph[v].isEmpty()) leaf[v] = 1; //자식이 없다면 그 노드는 리프 노드
for (int child : graph[v]) {
DFS(child,v);
leaf[v] += leaf[child];// 자식 노드의 리프 노드 개수를 현재 노드에 더함
}
}
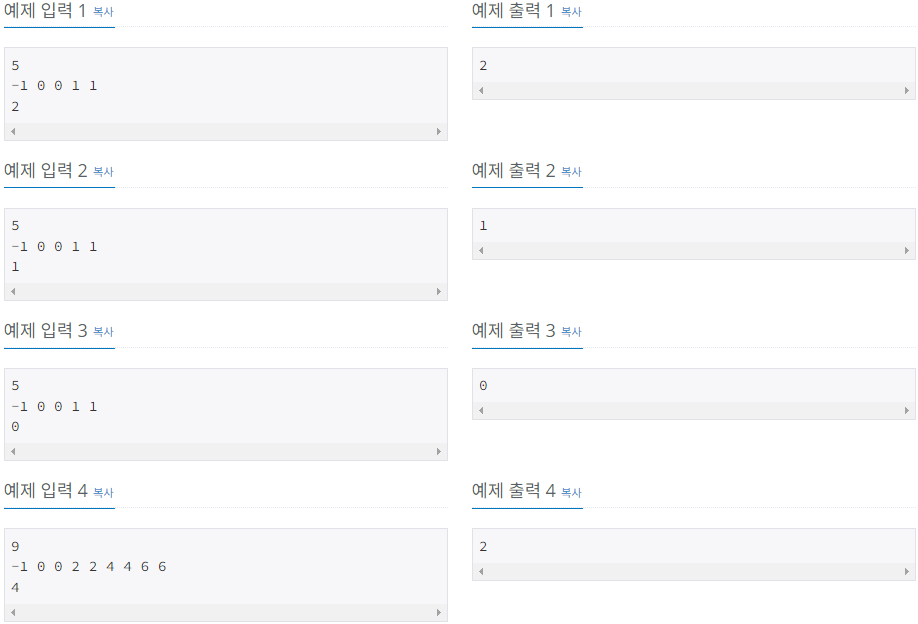
}예제 입력 1 (N=5, 부모 노드 = [-1 0 0 1 1], target=2)의 경우 출력이 어떻게 2가 나오는지 살펴보자.
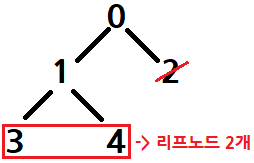
(1) 트리의 구성
- 0이 루트 노드
- 0의 자식: 1, 2
- 1의 자식: 3, 4
(2) 노드 2 삭제:
- grape[0]에서 2 제거
(3) DFS 수행:
- 0 방문: 자식 1
- 1 방문: 자식 3, 4
- 3 방문: 리프 노드 (leaf[3] = 1)
- 4 방문: 리프 노드 (leaf[4] = 1)
- 1로 돌아옴: leaf[1] = leaf[3] + leaf[4] = 2
- 0으로 돌아옴: leaf[0] = leaf[1] = 2
(4) 결과: 2 (리프 노드 개수)
다음으로 두 번째 풀이의 특징을 살펴보자.
-
부모와 자식 간의 양방향 그래프를 사용하였다.
-
삭제할 노드를 방문하지 않는 방식으로 처리하였다.
-
루트가 삭제 대상일 경우 즉시 0을 출력하고 종료한다.
-
전역 변수로 리프 노드 수를 직접 카운트한다.
두 번째 방법은 일반적인 그래프 탐색에 가깝기 때문에, 여러 유형에 쉽게 접근할 수 있다.
코드 2
import java.io.*;
import java.util.*;
public class Example1068_2 {
static ArrayList<Integer>[] graph;
static int[] parent;
static boolean[] visited;
static int N, target, answer; // N: 노드 개수, target: 삭제할 노드, root: 루트 노드
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine()); //N은 50보다 작거나 같은 자연수
graph = new ArrayList[N + 1]; //인접리스트 초기화 (리스트의 배열(또는 리스트의 리스트))
parent = new int[N + 1];
visited = new boolean[N + 1];
for (int i = 0; i < N; i++) {
graph[i] = new ArrayList<>();
}
int root = -1;
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
int parent = Integer.parseInt(st.nextToken());
if (parent == -1) {
root = i;
} else {
graph[i].add(parent);
graph[parent].add(i); // 서로 연결
}
}
target = Integer.parseInt(br.readLine()); //지울 노드의 번호
if (target == root) {
System.out.println(0);
return;
} else {
DFS(root);
}
System.out.println(answer);
}
static void DFS(int v) {
visited[v] = true;
int children = 0;
for (int current : graph[v]) {
if (current != target && !visited[current]) {
children++;
DFS(current);
}
}
if (children == 0) {
answer++; //자식노드가 없므면 리프노드
}
}
}