코딩테스트 관련 글을 포스팅할 때마다 문제와 함께 해당 알고리즘에 대해 정리했었는데, 세그먼트 트리 같은 경우에는 워낙 중요하기도 하고 어려운 개념이라 따로 포스팅하게 되었다.

세그먼트 트리

구간 합과 데이터 업데이트를 빠르게 수행하기 고안해낸 자료구조의 형태 (= 인덱스 트리)를 말한다.

세그먼트 트리 종류

• 구간 합
• 최대 최소 구하기

보통 세그먼트 트리 관련 문제가 나온다면, 구간 합 또는 최대 최소를 구하라는 문제이다.

구현 단계

1. 트리 초기화하기

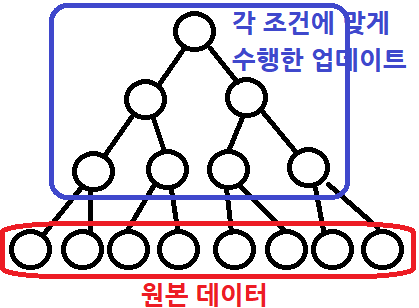
리프 노드만 원본 데이터 배열을 갖는다.

원본 데이터(=리프 노드)의 부모를 가지는 노드의 값은 앞서 말한대로 구간 합으로 도출된 값이거나 최대 최소로 도출된 값이다,

위 세그먼트 트리를 1차원 배열로 나타내는 작업이 필요하다.

순서대로 알아보자.

• 리프 노드의 개수가 데이터의 개수(N) 이상이 되도록 트리 배열을 만든다.
• 트리 배열 크기를 구하는 방법은 2^k >=N 을 만족하는 k의 최솟값을 구한 후 2^k*2 를 트리 배열의 크기로 정의하면 된다.

샘플 데이터
{5, 8, 4, 3, 7, 2, 1, 6}

• 위와 같은 샘플 데이터가 있다면 N=8이므로 2^3>=8 이므로 배열의 크기를 2^3*2=16 으로 정의한다.

• 리프노드에 원본 데이터를 입력한다. 이때 리프 노드의 시작위치를 트리 배열의 인덱스로 구해야 하는데, 구하는 방식은 2^k를 시작 인덱스로 취하면된다. 예를 들어 k가 3이면 시작 인덱스는 8이 된다.

• 8번 인덱스부터 리프노드 값들을 순서대로 기입한다.

• 리프 노드를 제외한 나머지 노드 값을 채운다 (2^k-1 부터 1번 쪽으로 채운다.)

• 채워야 하는 인덱스가 N이라고 가정하면 자신의 자식 노드를 이용해 해당 값을 채울 수 있다.

• 자식 노드의 인덱스는 이진 트리 형식이기 때문에 2N, 2N+1이 된다.

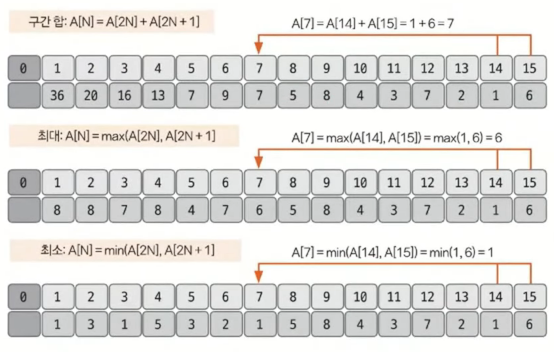
• 구간합은 뒤에서부터 탐색

  15/2=7, 7번 인덱스에 15번 인덱스 값인 6을 대입 | 14/2=7, 7번 인덱스에 14번 인덱스 값인 1을 대입 ⇒ 6+1=7 (7번 인덱스 값)

  13/2=6, 6번 인덱스에 13번 인덱스 값인 2를 대입 | 12/2=6, 6번 인덱스에 12번 인덱스 값인 7을 대입 ⇒ 2+7=9 (6번 인덱스 값)
  

• 최댓값도 뒤에서부터 탐색

  15/2=7, 7번 인덱스에 15번 인덱스 값인 6을 비교 | 14/2=7, 7번 인덱스에 14번 인덱스 값인 1을 비교⇒ max(6,1)=6 (7번 인덱스 값)

  13/2=6, 6번 인덱스에 13번 인덱스 값인 2를 비교 | 12/2=6, 6번 인덱스에 12번 인덱스 값인 7을 비교 ⇒ max(2,7)=7 (6번 인덱스 값)
  

• 최솟값도 뒤에서부터 탐색

  15/2=7, 7번 인덱스에 15번 인덱스 값인 6을 비교 | 14/2=7, 7번 인덱스에 14번 인덱스 값인 1을 비교⇒ min(6,1)=1 (7번 인덱스 값)

  13/2=6, 6번 인덱스에 13번 인덱스 값인 2를 비교 | 12/2=6, 6번 인덱스에 12번 인덱스 값인 7을 비교 ⇒ min(2,7)=2 (6번 인덱스 값)

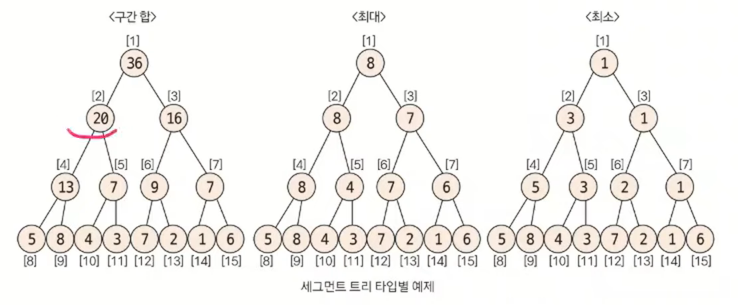
• 실제 트리 모양으로 구조화하면 위와 같이 표현된다.

• 구간합 : 특정 구간의 구간합 (2번 인덱스 값이 20인 이유: 4번 인덱스 값+5번 인덱스 값= 8번 인덱스 값+9번 인덱스 값+10번 인덱스 값+11번 인덱스 값)

• 최대: 특정 구간의 최댓값 (2번 인덱스 값이 8인 이유: Max(4번 인덱스 값, 5번 인덱스 값)= Max(8번 인덱스 값, 9번 인덱스 값, 10번 인덱스 값, 11번 인덱스 값)

• 최소: 특정 구간의 최솟값 (2번 인덱스 값이 8인 이유: Min(4번 인덱스 값, 5번 인덱스 값)= Max(8번 인덱스 값, 9번 인덱스 값, 10번 인덱스 값, 11번 인덱스 값)

2. 질의값 구하기

• 주어진 질의 인덱스를 세그먼트 트리의 리프 노드에 해당하는 인덱스로 변경

질의 인덱스를 세그먼트 트리 인덱스로 변경하는 방법

세그먼트 트리 index = 주어진 질의 index + 2^k - 1

위 샘플을 예제로 들어 k=3 이라면..

Q. 주어진 질의값이 1~3

A. 1+2^3-1=8 , 3+2^3-1=10 이므로 1에서 3인 질의값을 8에서 10의 질의값으로 변경해준다.

질의값 구하는 과정
(1) start_index % 2 == 1 일 때 해당 노드를 선택
(2) end_index % 2 == 0 일 때 해당 노드를 선택
(3) start_index depth 변경: start_indx = (start_index+1) / 2 연산 실행 //부모 노드
(4) end_index depth 변경: end_index = (end_index-1) / 2 연산 실행 //부모 노드
(5) (1)~(4)과정 반복하다 end_index < start_index가 되면 종료

• (1)~(2)에서 해당 노드를 선택했다는 것은 해당 노드의 부모가 나타내는 범위가 질의 범위를 넘어가기 때문에 해당 노드를 질의값에 영향을 미치는 독립 노드로 선택하고, 해당 노드의 부모 노드는 대상 범위에서 제외한다는 뜻.

  부모 노드를 대상 범위에서 제외하는 방법은 (3)~(4)에서 질의 범위에 해당하는 부모 노드로 이동하기 위해 인덱스 연산을 index/2가 아닌 (index+1)/2, (index-1)/2로 수행하는 것이다.

  질의에 해당하는 노드를 선택하는 방법은 구간 합, 최댓값 구하기, 최솟값 구하기 모두 동일하며 선택된 노드들에 관해 마지막에 연산하는 방식만 다르다.

샘플 데이터
{5, 8, 4, 3, 7, 2, 1, 6}

트리 초기화하기에서 나온 구간 합 샘플을 이용해 2-6번째 구간 합을 구하는 간단한 예제를 살펴보자.

먼저 리프노드의 인덱스로 변경하자.

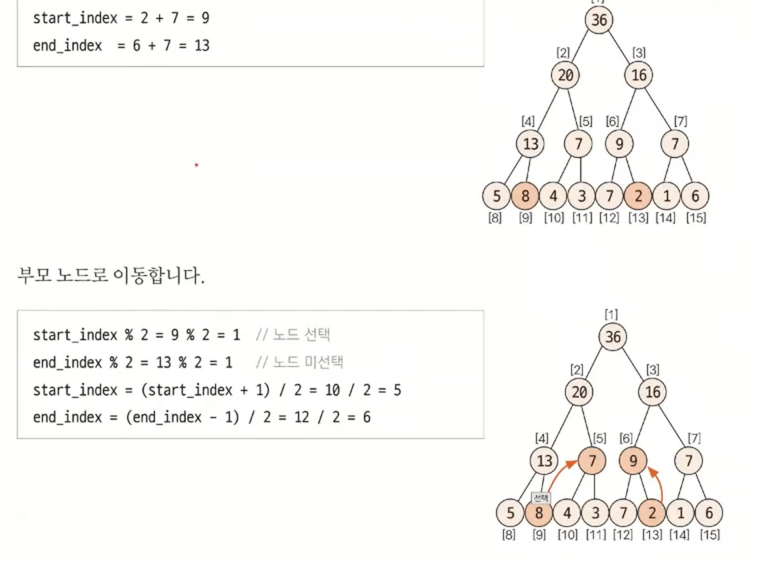
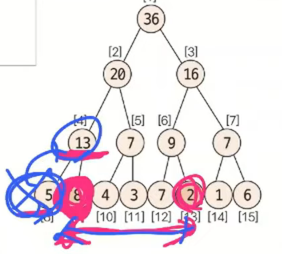
• start_index=9
  end_index=13
  인 구간을 구하려고 할때, 8번 인덱스는 구간에 포함되지 않기 때문에 8번 인덱스를 포함하고 있는 부모인 4번 인덱스는 필요하지 않다.

• 실제로 start_index % 2 = 1이기 때문에 위 그림처럼 오른쪽 노드에 위치하고 있다는 것을 알 수 있다. 이는 부모노드를 쓰면 안된다는 뜻이다.

  왜냐하면 해당 구간에 속하지 않는 노드의 값까지 부모노드가 가지고 있기 때문에 부모노드를 쓰면 안된다는 것이다.
  

• 부모 노드를 대상 범위에서 제외하는 방법은 부모노드 4번 인덱스 대신 바로 옆으로 뛰어 5번 노드로 이동한다. 여기서 도출된 식이 start_index = (start_index+1) / 2 이다.

  (start_index+1)을 하는 이유는 오른쪽에 있는 자식노드였다면 자신의 부모노드가 아닌 오른쪽에 있는 부모노드로 이동해야되기 때문이다.
  

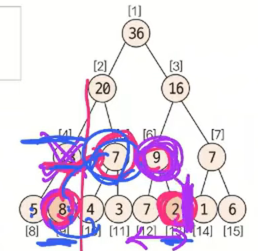
• 반대로 end_index(=13) % 2 = 1 이므로 부모노드 기준 오른쪽에 있는 자식노드이므로 그대로 자신의 부모노드로 이동한다. 이유는 end_index는 구간에서 마지막 노드이면서, 오른쪽에 위치한 자식노드이므로 부모노드가 자기 자신까지가 포함되어있는 데이터를 가지고 있기 때문이다.

  여기서 도출된 식이 end_indx = (end_index-1) / 2 이다.

end_index < start_index 이므로 종료하고 값을 구한다. 2~6번 구간 합의 값은 선택된 노드의 합인 8+9+7 =24이다.

3. 데이터 업데이트하기

다음은 5번 데이터의 값을 7에서 10으로 업데이트하는 예시이다. 5번 데이터의 인덱스를 리프 노드 인덱스로 변경하면 5+7=12 이므로 12번 노드의 값이 업데이트된다.

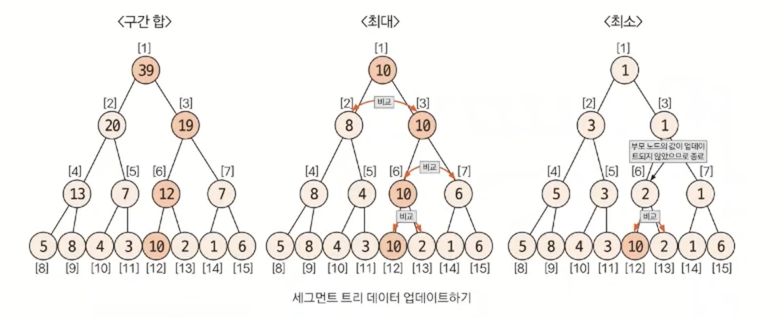
트리특성을 살려 이진트리가 부모로 갈 때 나누기 2(/2)를 하며 부모노드로 올라가면서 구간합,최대 최소 값 구하기 등을 진행한다.