신입수행 과제였던 8퍼즐 문제를 이용한 A* 알고리즘 구현과제에 대해 정리하고자 포스팅을 준비했다.
A* Algorithm
A* 알고리즘
주어진 출발 꼭짓점에서부터 목표 꼭짓점까지 가는 최단 경로를 찾아내는 그래프 탐색 알고리즘 중 하나이다.
이 알고리즘은 다익스트라 알고리즘과 유사하나 차이점은 각 꼭짓점 x에 대해 그 꼭짓점을 통과하는 최상의 경로를 추정하는 순위값인 휴리스틱 추정값 h(n)을 매기는 방법을 이용한다는 것이다.
휴리스틱 추정값
가용한 정보를 기반으로 각 분기 단계에서 어느 한 분기를 선택하기 위해 사용하는 다양한 탐색 알고리즘의 대안 함수이다.
방법은 두 가지로 나눌 수 있다.
(1) 잘못 배치된 타일의 수를 세는 것
(2) 각 블록의 현재 위치와 목표 위치 사이의 Manhattan distance(맨하탄 거리)의 합을 구하는 것
다시 한번 말하자면 A* 알고리즘은 출발 꼭짓점으로부터 목표 꼭짓점까지 최적 경로를 탐색하기 위한 것이다.
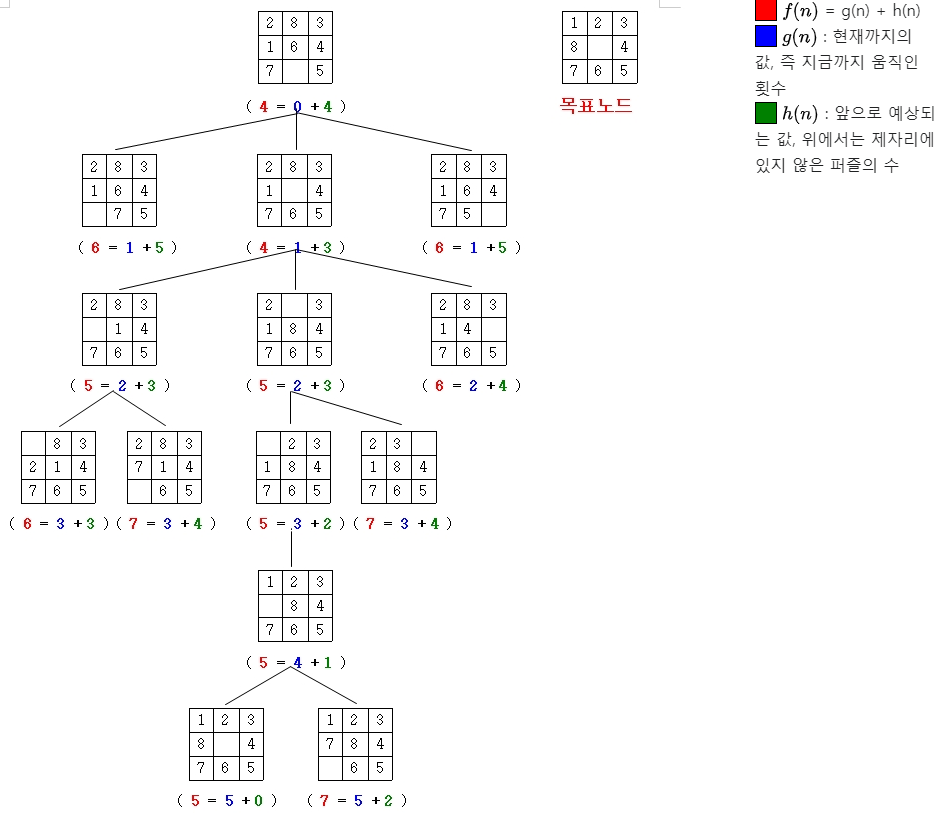
이를 위해서는 각각의 꼭짓점에 대한 평가 함수를 정의해야 한다. 평가함수 f(n)은 다음과 같다.
f(n) = g(n) + h(n)
- g(n): 출발 꼭짓점으로부터 꼭짓점 n까지의 경로 가중치
- h(n): 꼭짓점 n으로부터 목표 꼭짓점까지의 추정 경로 가중치
이 f(n)이 작은 값부터 탐색하는 특성 상 우선순위 큐가 사용된다.
동작 순서는 다음과 같다.
-
f(x)를 오름차순 우선순위 큐에 노드로 삽입한다. -
우선순위 큐에서 최우선 노드를 꺼낸다.
-
해당 노드에서 이동할 수 있는 노드를 찾는다.
-
그 노드들의
f(x)를 구한다. -
그 노드들을 우선순위 큐에 삽입한다.
-
목표 노드에 도달할 때까지 반복한다
이 부분이 다익스트라 알고리즘과 유사점이 존재한다.
다익스트라 알고리즘과의 유사점
1. 우선순위 큐 사용
다익스트라: 최소 거리를 가진 노드를 선택하기 위해 우선순위 큐를 사용한다.
A*: 우선순위 큐를 사용해 f(n) 값이 가장 작은 노드를 선택한다.2. 그리디한 접근
다익스트라: 항상 현재까지 알려진 최단 경로를 선택한다.
A*: f(n) = g(n) + h(n)이 최소인 노드를 선택하여 탐색한다.3. 방문 노드 관리
다익스트라와 A* 모두 이미 방문한 노드를 다시 방문하지 않는다.
예시: 8-Puzzle
-
3x3 숫자판에 1~8까지의 숫자와 빈칸이 주어져 있다고 가정
-
숫자를 인접한 빈칸으로 옮기는 작업을 반복함으로써 주어진 숫자 배열로부터 목표가 되는 숫자 배열로 바꾸되, 숫자의 총 이동 횟수를 최소로 한다.
-
이를
A* 알고리즘으로 풀어보자
코드
먼저 전체 코드는 다음과 같다.
import java.io.*;
import java.util.*;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static String startNode;
static String goalNode;
static int[] moveRow = {-1, 0, 1, 0};
static int[] moveCol = {0, 1, 0, -1};
static HashMap<String, Integer> visitMap = new HashMap<>(); //한 번의 테스트 시 방문 여부 체크: 순서X 중복(키X,값O)
static PriorityQueue<Puzzle> pq = new PriorityQueue<>();
public static void main(String[] args) throws IOException {
System.out.println("아래에 목표 노드를 3x3 형태로 입력해주세요. (빈 퍼즐은 숫자 대신 #을 입력해주세요)"); //목표 노드 입력
StringBuilder sbGoalBoard = new StringBuilder();
for (int i = 0; i < 3; i++) {
sbGoalBoard.append(br.readLine());
}
goalNode = sbGoalBoard.toString();
System.out.println("아래에 시작 노드를 3x3 형태로 입력해주세요. (빈 퍼즐은 숫자 대신 #을 입력해주세요)"); //시작 노드 입력
StringBuilder sbStartBoard = new StringBuilder();
for (int i = 0; i < 3; i++) {
sbStartBoard.append(br.readLine());
}
startNode = sbStartBoard.toString();
//시작 노드 우선순위_큐에 담음 (f(n)=g(n)+h(n)이지만, g(n)이 0이므로 f(n)에는 h(n)만 대입)
pq.add(new Puzzle(startNode, getHeuristic(startNode), 0, getHeuristic(startNode)));
//시작 노드 재방문_방지_map에 저장
visitMap.put(startNode, 0);
boolean reachedGoal = aStar(); //a* 알고리즘
if (reachedGoal) {
bw.write(String.valueOf("최소한의 이동 횟수: "+visitMap.get(goalNode)+ "\n"));
} else {
bw.write("해당 시작노드는 목표노드로 이동할 수 없습니다." + "\n");
}
bw.flush();
bw.close();
}
private static boolean aStar() throws IOException {
StringBuilder stepsLog = new StringBuilder(); // 성공 시 출력할 로그를 저장
stepsLog.append("\n");
while (!pq.isEmpty()) {
Puzzle currentPuzzle = pq.poll();
String currentData = currentPuzzle.node;
int currentStep = currentPuzzle.g; // 현재 노드의 깊이
if (currentData.equals(goalNode)) {
//목표 노드까지 stringbuilder에 추가
consoleLog(stepsLog, currentPuzzle, goalNode);
stepsLog.append("\n");
bw.write(stepsLog.toString());
// 목표 상태에 도달했을 때만 로그를 출력
bw.write("목표 상태에 도달했습니다!\n");
return true;
}
//시작 노드부터 목표노드 이전까지 선택된 노드를 stringbuilder에 추가
consoleLog(stepsLog, currentPuzzle, currentData);
int emptyPlaceIndex = currentData.indexOf("#");
int currentRow = emptyPlaceIndex / 3;
int currentCol = emptyPlaceIndex % 3;
for (int i = 0; i < 4; i++) {
int newRow = currentRow + moveRow[i];
int newCol = currentCol + moveCol[i];
if (newRow >= 0 && newRow < 3 && newCol >= 0 && newCol < 3) {
StringBuilder nextData = new StringBuilder(currentData);
nextData = swap(currentRow, currentCol, newRow, newCol, nextData);
String data = nextData.toString();
if(visitMap.containsKey(data)) continue; //이미 본 케이스라면 건너뛴다.
else {
int g = currentStep + 1; //경로가중치+1
int h = getHeuristic(data);
int f = g + h;
pq.add(new Puzzle(data, f, g, h));
visitMap.put(data, g);
}
}
}
}
return false;
}
private static void consoleLog(StringBuilder stringBuilder, Puzzle currentPuzzle, String data) {
stringBuilder.append("(1) f(n): " + currentPuzzle.f+", g(n): " + currentPuzzle.g+", h(n): " + currentPuzzle.h).append("\n");
stringBuilder.append("(2) 이동 횟수: " + currentPuzzle.g).append("\n");
for (int i = 0; i < 3; i++) {
stringBuilder.append(data.substring(i * 3, i * 3 + 3)).append("\n");
}
stringBuilder.append("---------").append("\n");
}
private static int getHeuristic(String data) {
// 목표노드 인덱스 위치의 숫자 값이 동일한지 확인 (h(n)은 작을 수록 좋은 것)
// 휴리스틱 방법 Manhattan Distance로 해도 상관없음
int cnt = 0;
for (int i = 0; i < data.length(); i++) {
if(data.charAt(i) == '#') continue;
else if (goalNode.charAt(i) != data.charAt(i)) cnt++; //같은 위치에 같은 숫자가 아니라면 cnt++
}
return cnt;
}
private static StringBuilder swap(int currentRow, int currentCol, int newRow, int newCol, StringBuilder nextData) {
int currentRC = currentRow * 3 + currentCol; //이차원 배열의 row, col 을 nextData에서 추출 가능하게 일차원 형태로 변환 (빈공간 위치 인덱스)
int nextRC = newRow * 3 + newCol; //이차원 배열의 row, col 을 nextData에서 추출 가능하게 일차원 형태로 변환 (변경할 값이 있는 인덱스)
char temp = nextData.charAt(currentRC);
nextData.setCharAt(currentRC, nextData.charAt(nextRC));
nextData.setCharAt(nextRC, temp);
return nextData;
}
static class Puzzle implements Comparable<Puzzle>{
String node;
int f; //f(n)
int g; //g(n)
int h; //h(n)
@Override
public int compareTo(Puzzle o) {
if(f == o.f) return Integer.compare(g, o.g); //f(n)이 동일하다면 이동 횟수가 작은 수 선택
return Integer.compare(f, o.f); //f(n)기준으로 작은 수 선택
}
public Puzzle(String node, int f, int g, int h) {
this.node = node;
this.f = f;
this.g = g;
this.h = h;
}
}
}전제
-
목표 노드와 시작 노드를 입력받는다.
- 단, 빈 퍼즐은 숫자 대신 #을 쓴다 (
1~8+#)
- 단, 빈 퍼즐은 숫자 대신 #을 쓴다 (
-
시작 노드에서 목표 노드로 도달하는데 있어 이동 횟수 및 퍼즐 이동 형태를 콘솔로 출력한다.
-
마지막엔 최소 이동 횟수를 출력한다.
-
이동이 불가능한 경우엔 이동 횟수 및 퍼즐 이동 형태를 생략하고, 이동 불가 메세지를 출력한다.
해결과정
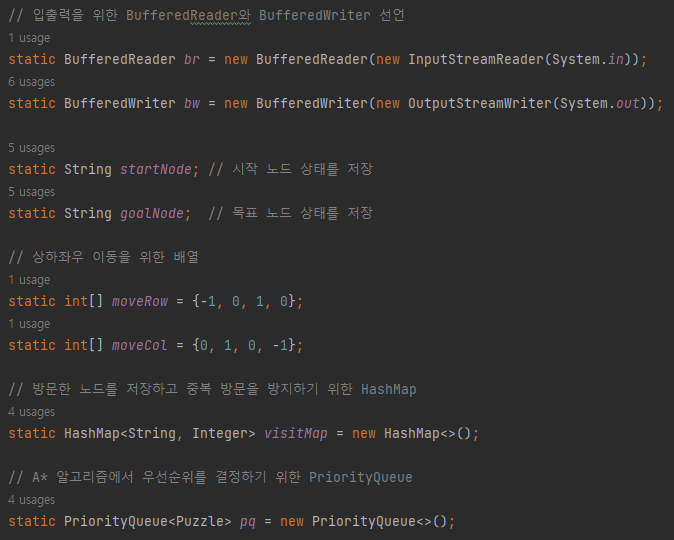
- 정적 멤버(=클래스 멤버)로 선언한 변수들
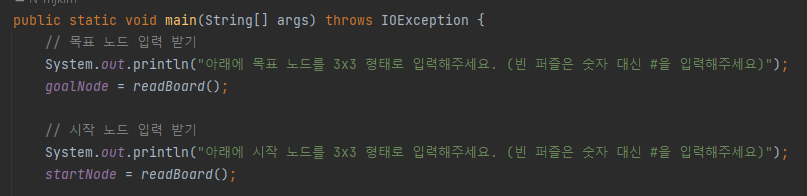
- 입력 받은 목표 노드와 시작 노드를 한 줄의 문자열로 바꾼다.

-
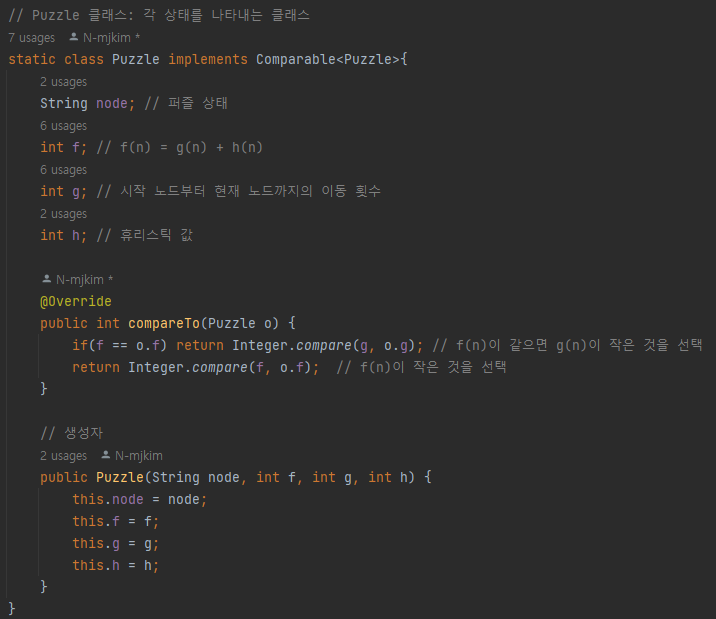
문자열 형태의 시작 노드를 우선순위 큐에 담아 주었다. (시작 노드(String), f(n), g(n), h(n))
참고로 우선 순위 큐인 PriorityQueue는 f(n) 값이 가장 작은 노드가 우선권을 가지게 한다.
f(n) 값이 동일한 노드끼리인 경우 g(n)이 더 작은 노드가 우선권을 가진다.


-
HashMap을 활용하여 재방문을 방지한다.
(key: 문자열 형태의 노드 값, value: 경로 가중치(=이동 횟수)인 g(n))
-
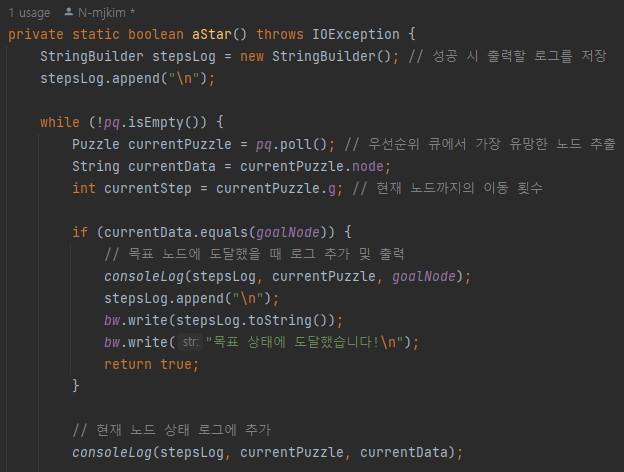
while문을 사용하여 우선순위 큐가 빌 때까지 현재 빈 퍼즐과 자리를 바꿀 수 있는 숫자의 위치를 바꿔준다.
만약 HashMap을 통해 이전 방문한 형태라면 건너 뛴다.
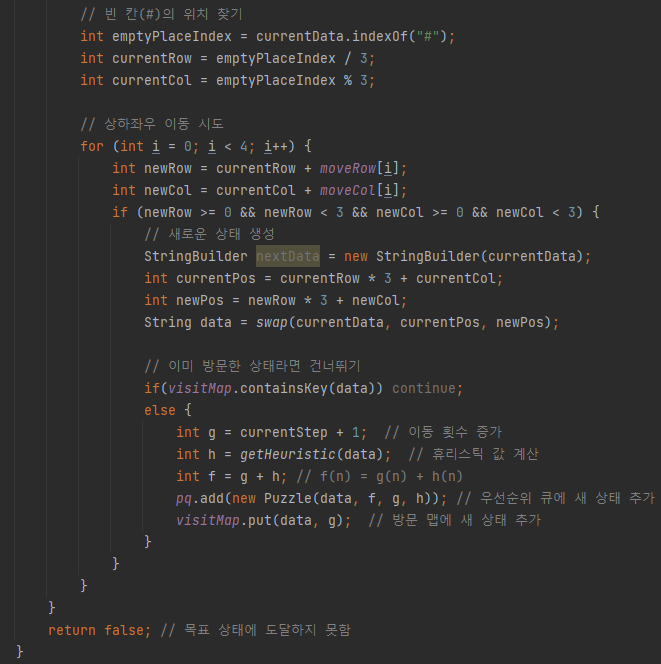
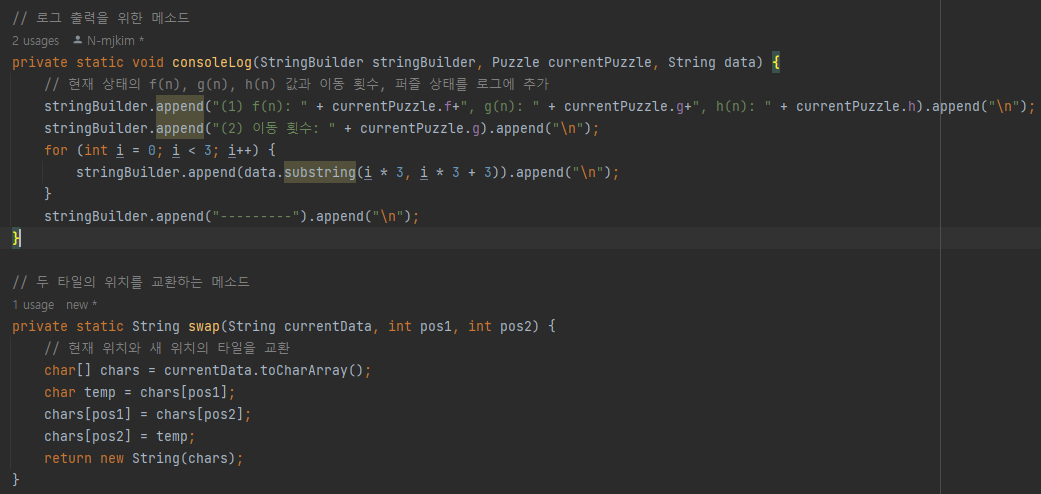
-
현재 노드의 g(n)과 h(n)을 더해서 f(n)을 구한다.
휴리스틱 값인 h(n)은 잘못 배치된 타일의 수를 세는 것과
각 블록의 현재 위치와 목표 위치 사이의 Manhattan distance(맨하탄 거리)의 합을 구하는 것 두 가지 방법이 있으나,
필자는 잘못 배치된 타일의 수를 세는 방법을 채택하였다.
참고로 빈공간은 제외하고 세야 되기 때문에 빈공간이라고 가정한 문자
#이라면 for문으로 돌아갈 수 있게 continue 키워드를 썼다.
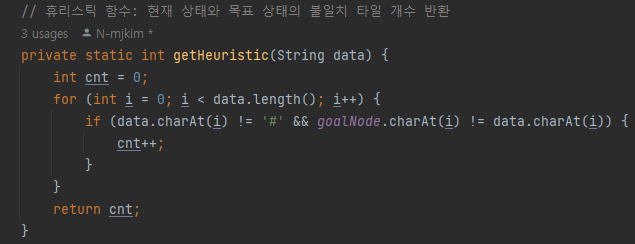
-
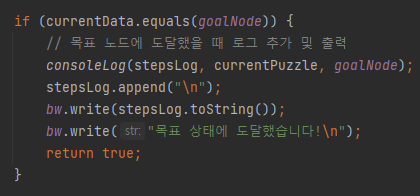
퍼즐의 자리를 바꾸기 전에 우선순위 큐에서 꺼낸 노드의 값이 목표 노드와 같다면 목표 상태에 도달했다는 문구와 함께 최소한의 이동 횟수(=g(n))을 출력한다.
만약 목표 노드로 도달할 수 없다면 이동 불가 메세지를 출력한다.

시뮬레이션
위에 예시 그림에 목표 노드
123
8#4
765그리고 시작 노드
283
164
7#5를 가지고 작성된 소스코드를 실행해보자.
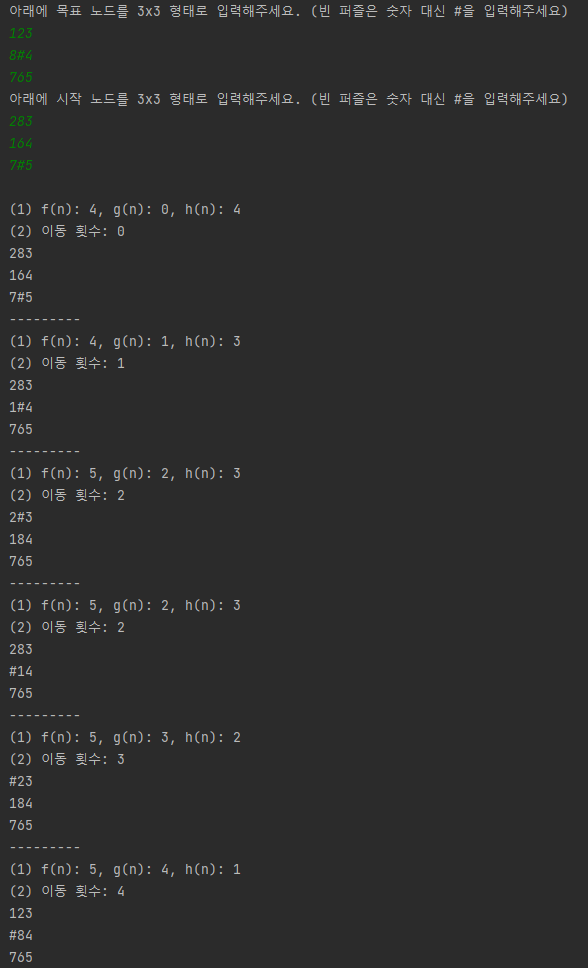
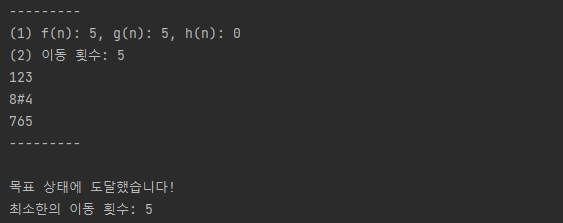
예시에서 시작 노드에서 출발해 가지치기를 시작하게 되면 f(n)이 가장 작은 값을 선택해 또 가지치기를 하며 목표노드로 도달하기 위해 최적의 경로를 도출해내고 있다.
실패 시엔 다음과 같이 콘솔에 출력된다.