00. 깊이 우선 탐색(DFS) & 너비 우선 탐색(BFS)
그래프란?
정점과 간선으로 이루어진 자료구조의 일종. G = (V, E)
V: 그래프의 정점(=그래프의 노드) 집합
E: 간선(=노드를 연결하는 선) 집합
그래프 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것 (특정 개체 A를 찾기 위한 알고리즘)
Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지
대표적인 문제 유형
- 경로탐색 유형 (최단거리, 시간)
- 네트워크 유형 (연결)
- 조합 유형 (모든 조합 만들기)
< 프로그래머스에 올라오는 DFS/BFS 문제 >
깊이 우선 탐색 (DFS, Depth-First Search)의 개념
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
-
미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함
-
즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함
-
모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
-
깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
-
검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
= 즉, 한 놈만 끝까지 패는 유형 : 재귀함수가 가장 일반적
깊이 우선 탐색(DFS)의 특징
자기 자신을 호출하는 순환 알고리즘의 형태를 지님
이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것
(이를 검사하지 않을 경우 무한루프에 빠질 위험이 있음)
깊이 우선 탐색(DFS)의 과정
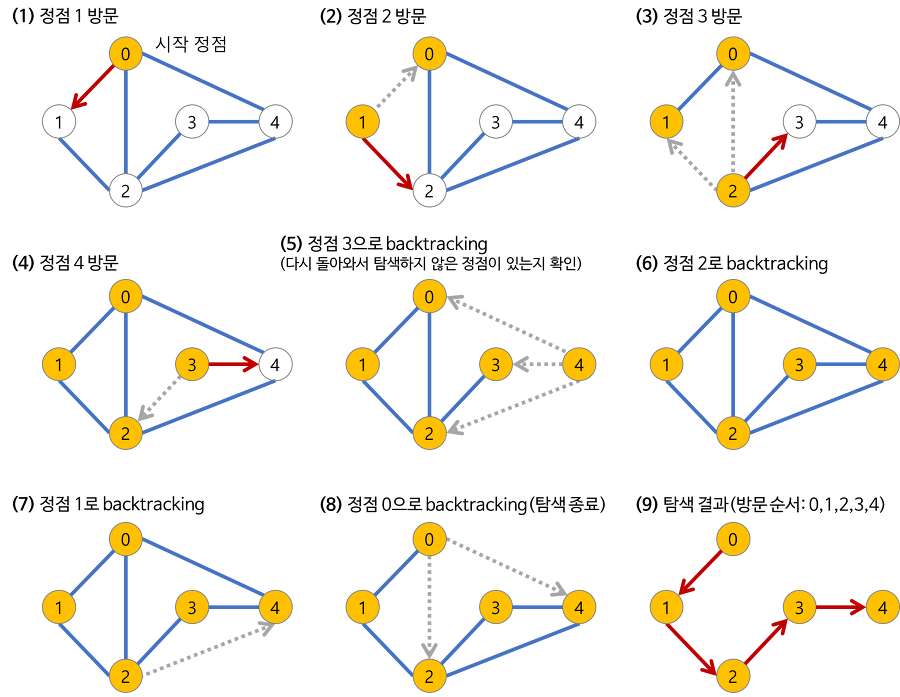
깊이 우선 탐색(DFS)의 시간 복잡도
DFS는 그래프(정점의 수 : N, 간선의 수: E)의 모든 간선을 조회함
-
인접 리스트로 표현된 그래프 : O(N+E)
-
인접 행렬로 표현된 그래프 : O(N^2)
너비 우선 탐색 (BFS, Breadth-First Search)
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
-
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
-
즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것
-
두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함
ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Ash 와 Vanessa 사이에 존재하는 경로를 찾는 경우
-
깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야할지도 모름
-
너비 우선 탐색의 경우 - Ash와 가까운 관계부터 탐색
= 여러 놈을 한대씩 때리면서 가는 유형 : Queue/LinkedList 사용하는 것이 보편적
너비 우선 탐색(BFS)의 특징
-
BFS 는 재귀적으로 동작하지 않는다.
-
이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것이다 이를 검사하지 않을 경우 무한 루프에 빠질 위험이 있다.
-
BFS 는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용함
-
즉 선입선출(FIFO) 원칙으로 탐색
예제 )
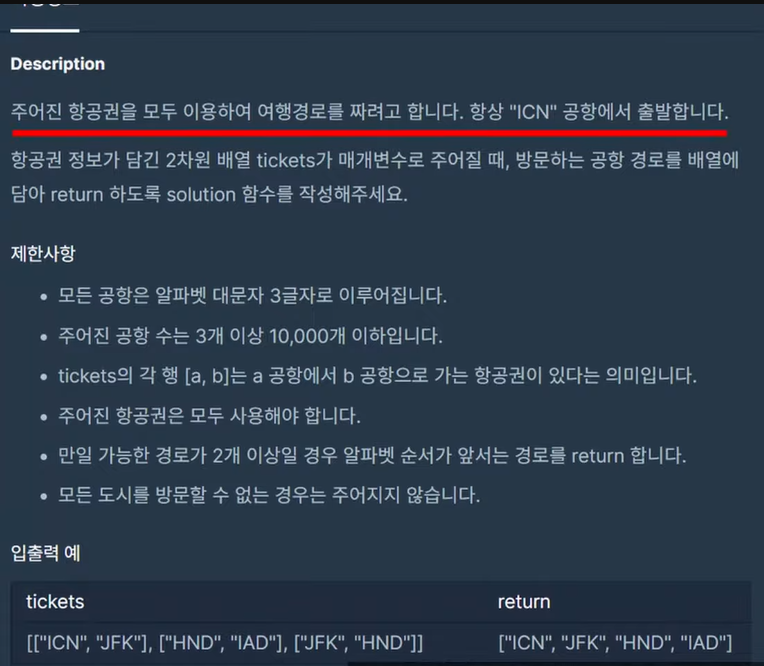
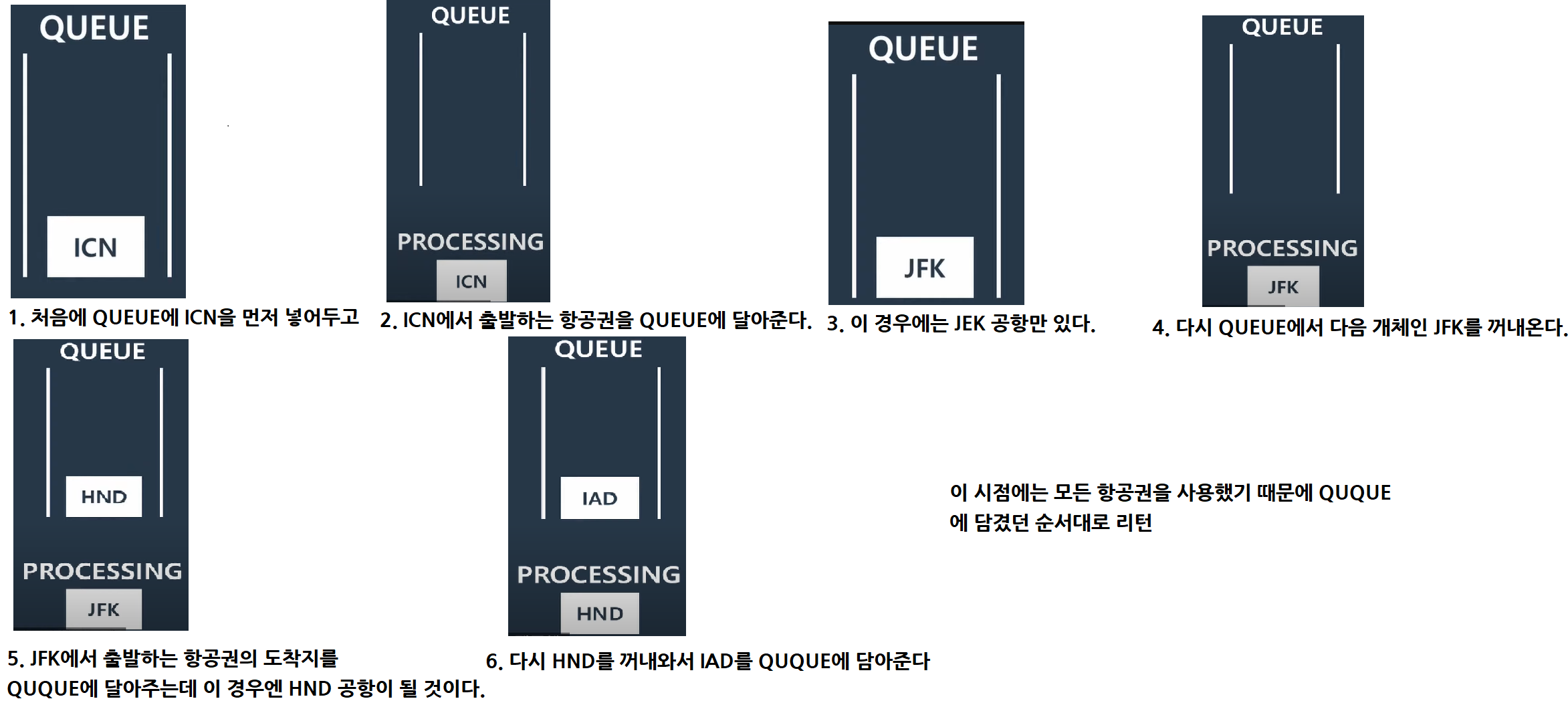
- 가장 먼저 넣었던 것을 꺼내서
- 연결된 점을 Queue에 넣기
- Queue가 빌 때까지 반복
=> 순서가 보장되어야 하기 때문에 Queue나 LinkedList를 쓰는 것이 보편적
너비 우선 탐색(BFS)이 과정
- 깊이가 1인 모든 노드를 방문하고 나서 그 다음에는 깊이가 2인 모든 노드를, 그 다음에는 깊이가 3인 모든 노드를 방문하는 식으로 계속 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마친다.
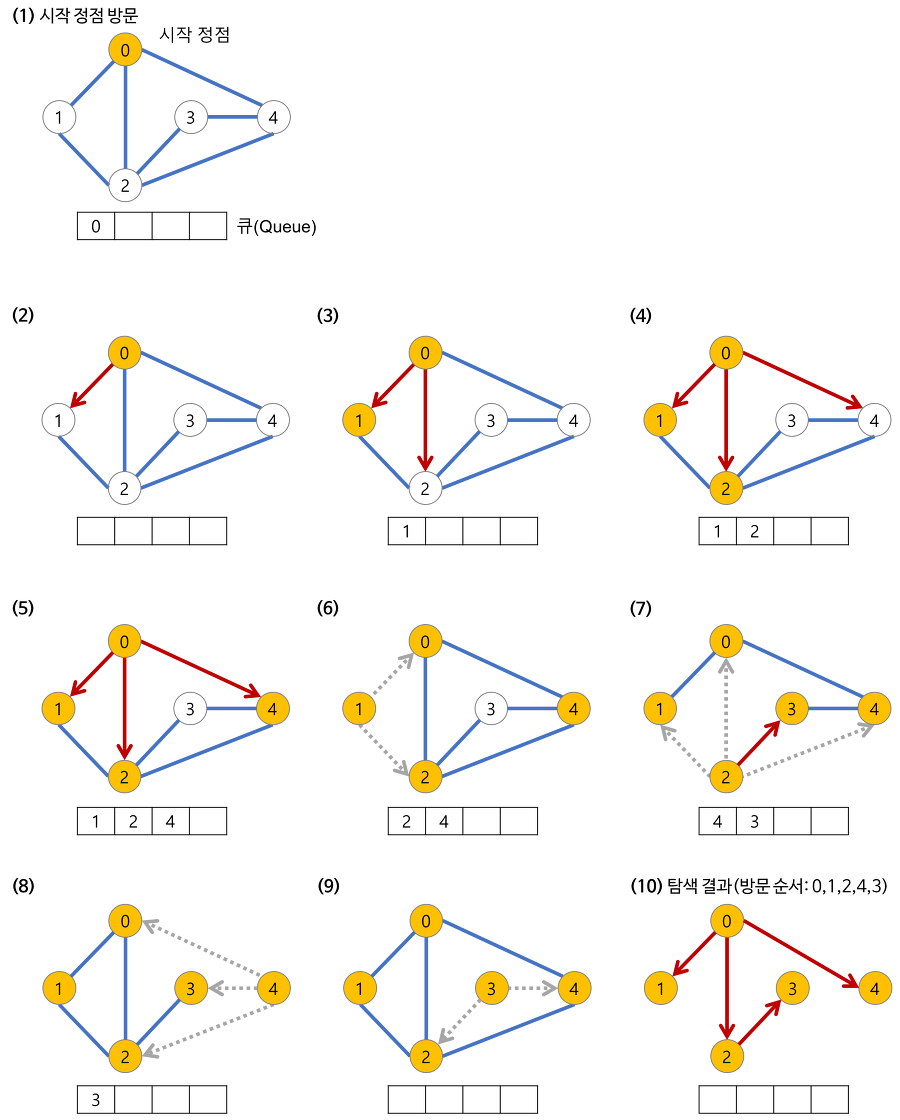
DFS 와 BFS 의 차이

DFS와 BFS를 선택하는 기준을 세워보면 다음과 같다.
앞쪽에 쉬운 문제로 나왔다면 빠르게 DFS로 푸는 것을 추천
뒤쪽에 난이도가 있는 문제거나 DFS로 풀기에는 너무 오래걸릴 것 같다면 BFS로 풀자
01. 재귀함수
설명
자연수 N이 입력되면 재귀함수를 이용하여 1부터 N까지를 출력하는 프로그램을 작성하세요.
입력
첫 번째 줄은 정수 N(3<=N<=10)이 입력된다.
출력
첫째 줄에 출력한다.
예시 입력 1
3
예시 출력 1
1 2 3
코드
import java.util.Scanner;
//재귀함수
public class Main {
public void DFS(int n) {
if(n==0) return;
else {
DFS(n - 1);
System.out.print(n + " ");
}
}
public void solution(int n) {
DFS(n);
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
T.solution(n);
}
}
02. 재귀함수를 이용한 이진수 출력
설명
10진수 N이 입력되면 2진수로 변환하여 출력하는 프로그램을 작성하세요. 단 재귀함수를 이용해서 출력해야 합니다.
입력
첫 번째 줄에 10진수 N(1<=N<=1,000)이 주어집니다.
출력
첫 번째 줄에 이진수를 출력하세요
예시 입력 1
11
예시 출력 1
1011
초기에 푼 코드
package section7;
import java.util.Scanner;
//재귀함수를 이용한 이진수 출력
public class ExampleTwo1 {
public String solution(int n, String answer) {
int a = 0, b = 0;
if (n != 1) {
a = n / 2;
}
b = n % 2;
answer += b;
if (n == 1) {
answer = new StringBuilder(answer).reverse().toString();
return answer;
}
a = n / 2;
return solution(a,answer);
}
public static void main(String[] args) {
ExampleTwo1 T = new ExampleTwo1();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
System.out.println(T.solution(n,""));
}
}
최종코드

package section7;
import java.util.Scanner;
//재귀함수를 이용한 이진수 출력
public class ExampleTwo2 {
public void solution(int n) {
if(n==0) return;
else{
solution(n/2);
System.out.println(n%2 + " ");
}
}
public static void main(String[] args) {
ExampleTwo2 T = new ExampleTwo2();
T.solution(11);
}
}
03. 팩토리얼
설명
자연수 N이 입력되면 N!를 구하는 프로그램을 작성하세요.
예를 들어 5! = 54321=120입니다.
입력
첫 번째 줄에 자연수 N(1<=N<=10)이 주어집니다.
출력
첫 번째 줄에 N팩토리얼 값을 출력합니다.
예시 입력 1
5
예시 출력 1
120
코드
import java.util.Scanner;
//팩토리얼
public class Main {
public int solution(int n) {
if(n==1) return 1;
else {
return n * solution(n-1);
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
System.out.println(T.solution(n));
}
}04. 피보나치 수열
설명
1) 피보나치 수열을 출력한다. 피보나치 수열이란 앞의 2개의 수를 합하여 다음 숫자가 되는 수열이다.
2) 입력은 피보나치 수열의 총 항의 수 이다. 만약 7이 입력되면 1 1 2 3 5 8 13을 출력하면 된다.
입력
첫 줄에 총 항수 N(3<=N<=45)이 입력된다.
출력
첫 줄에 피보나치 수열을 출력합니다
예시 입력 1
10
예시 출력 1
1 1 2 3 5 8 13 21 34 55
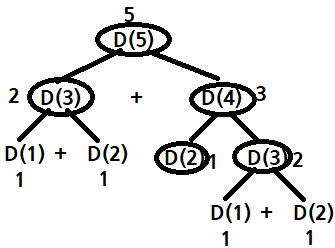
코드1
package section7;
import java.util.Scanner;
//피보나치 수열
public class ExampleFour {
public int solution(int n) {
if(n == 1) return 1;
else if (n == 2) return 1;
else return solution(n - 1) + solution(n - 2);
}
public static void main(String[] args) {
ExampleFour T = new ExampleFour();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
for(int i=1;i<=n;i++) System.out.print(T.solution(i)+" ");
}
}
입력되는 수가 커지면 수많은 가지치기로 출력하는데 너무 많은 시간이 소요된다.
이를 더 빨리하기 위해 배열에 저장해놓고 다시 호출될때 사용하자
메모이제이션(memoization) 이란
값비싼 함수 호출의 결과를 캐싱하고 동일한 입력이 다시 발생할 때 불필요하게 다시 계산하는 대신 캐싱된 결과를 반환하는 프로그래밍 기술
동일한 입력으로 여러 번 호출되는 함수나 컴포넌트가 있을 때 유리
코드2
import java.util.Scanner;
//피보나치 수열
public class Main {
static int[] fibo;
public int solution(int n) {
//fibo의 인덱스 n의 값이 0보다 크다면 저장했음을 나타냄으로 해당 값을 리턴 -> 속도개선
if(fibo[n]>0) return fibo[n];
if(n == 1) return fibo[n]=1;
else if (n == 2) return fibo[n]=1;
else return fibo[n] = solution(n - 1) + solution(n - 2);
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n = kb.nextInt();
fibo = new int[n + 1];
T.solution(n);
for(int i=1;i<=n;i++) System.out.print(fibo[i]+" ");
}
}
05. 이진트리 순회(깊이우선탐색)
설명
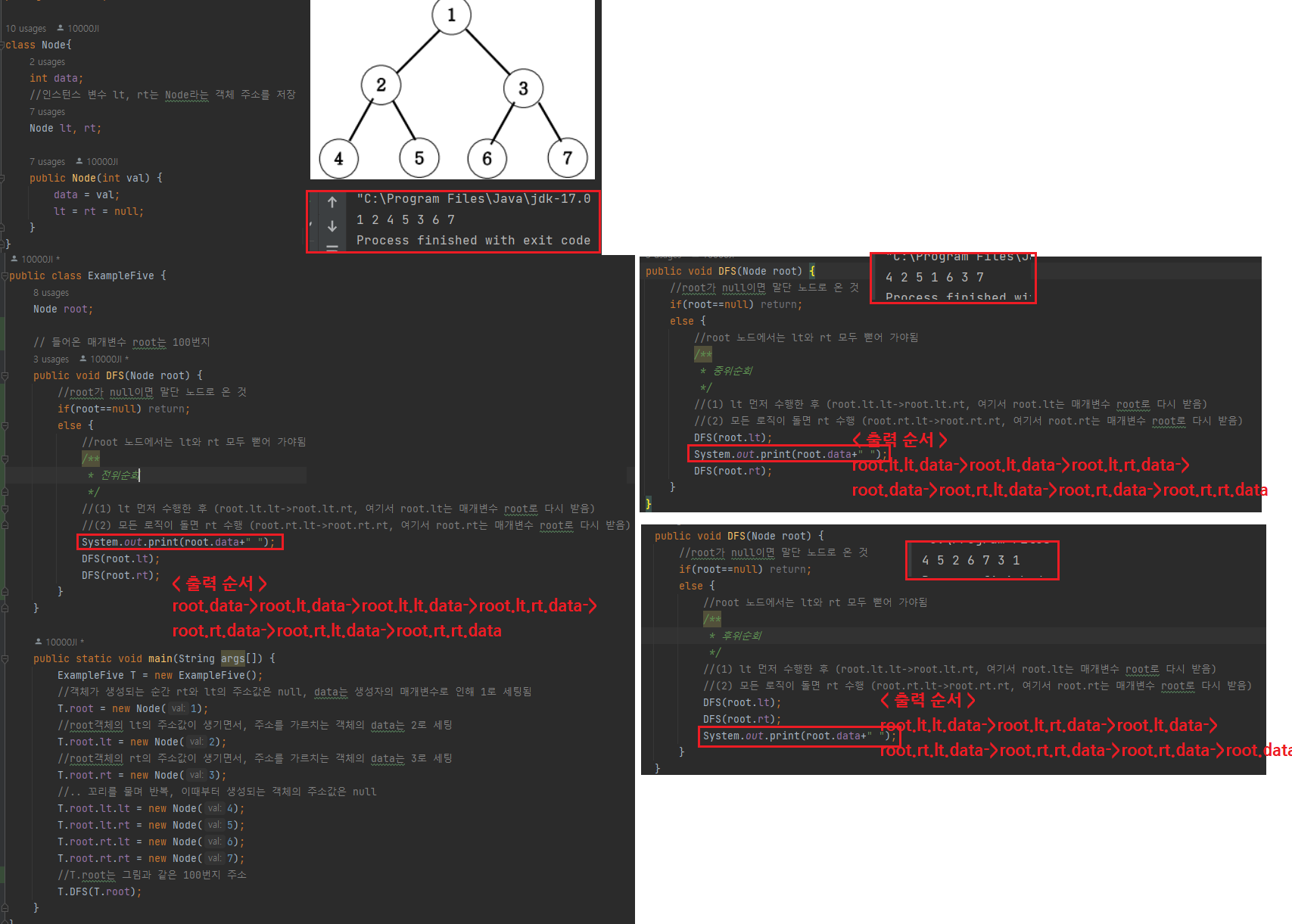
아래 그림과 같은 이진트리를 전위순회와 후위순회를 연습해보세요.
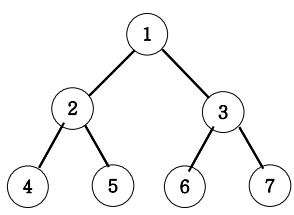
전위순회 출력 : 1 2 4 5 3 6 7
중위순회 출력 : 4 2 5 1 6 3 7
후위순회 출력 : 4 5 2 6 7 3 1
추가설명
전위순회는 부모 -> 왼쪽 자식-> 오른쪽 자식 으로 순회
중위순회는 왼쪽 자식 -> 부모-> 오른쪽 자식 으로 순회
후위순회는 왼쪽 자식 -> 오른쪽 자식 -> 부모 로 순회
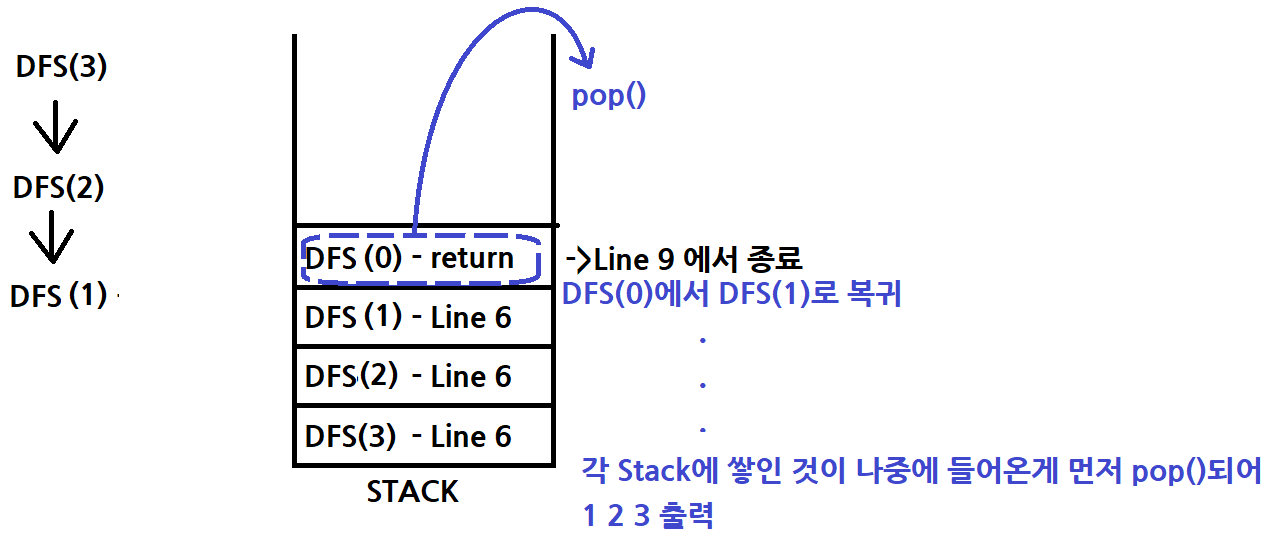
< main 부분 >
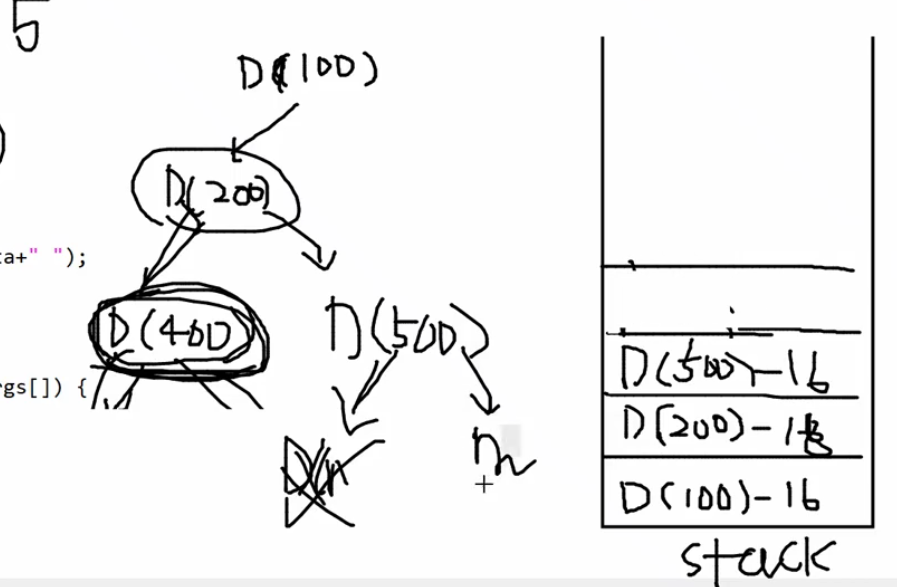
<직접 그림을 그려 stack을 쌓아보는 것을 추천 >
코드
전위순회 코드
package section7;
class Node{
int data;
//인스턴스 변수 lt, rt는 Node라는 객체 주소를 저장
Node lt, rt;
public Node(int val) {
data = val;
lt = rt = null;
}
}
//이진트리 순회(깊이우선탐색)
public class ExampleFive {
Node root;
// 들어온 매개변수 root는 100번지
public void DFS(Node root) {
//root가 null이면 말단 노드로 온 것
if(root==null) return;
else {
//root 노드에서는 lt와 rt 모두 뻗어 가야됨
/**
* 전위순회
*/
//(1) lt 먼저 수행한 후 (root.lt.lt->root.lt.rt, 여기서 root.lt는 매개변수 root로 다시 받음)
//(2) 모든 로직이 돌면 rt 수행 (root.rt.lt->root.rt.rt, 여기서 root.rt는 매개변수 root로 다시 받음)
System.out.print(root.data+" ");
DFS(root.lt);
DFS(root.rt);
}
}
public static void main(String args[]) {
ExampleFive T = new ExampleFive();
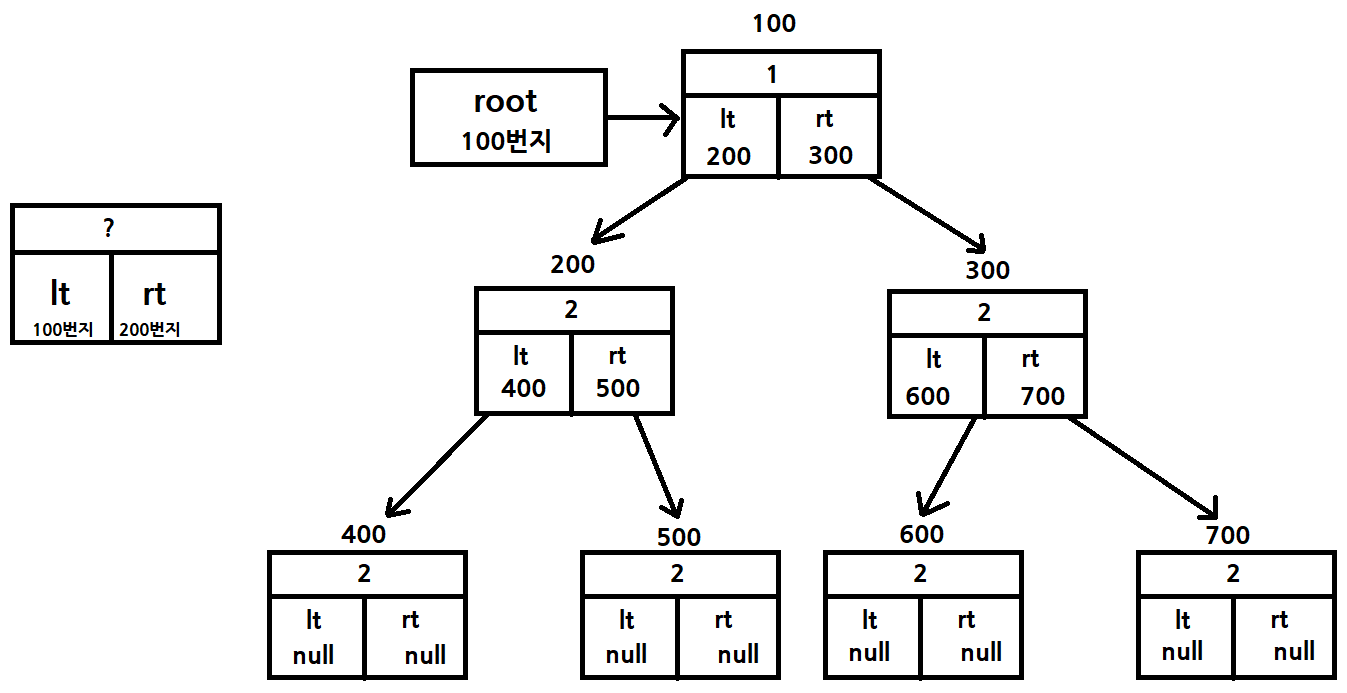
//객체가 생성되는 순간 rt와 lt의 주소값은 null, data는 생성자의 매개변수로 인해 1로 세팅됨
T.root = new Node(1);
//root객체의 lt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 2로 세팅
T.root.lt = new Node(2);
//root객체의 rt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 3로 세팅
T.root.rt = new Node(3);
//.. 꼬리를 물며 반복, 이때부터 생성되는 객체의 주소값은 null
T.root.lt.lt = new Node(4);
T.root.lt.rt = new Node(5);
T.root.rt.lt = new Node(6);
T.root.rt.rt = new Node(7);
//T.root는 그림과 같은 100번지 주소
T.DFS(T.root);
}
}
중위순회 코드
package section7;
class Node{
int data;
//인스턴스 변수 lt, rt는 Node라는 객체 주소를 저장
Node lt, rt;
public Node(int val) {
data = val;
lt = rt = null;
}
}
//이진트리 순회(깊이우선탐색)
public class ExampleFive {
Node root;
// 들어온 매개변수 root는 100번지
public void DFS(Node root) {
//root가 null이면 말단 노드로 온 것
if(root==null) return;
else {
//root 노드에서는 lt와 rt 모두 뻗어 가야됨
/**
* 중위순회
*/
//(1) lt 먼저 수행한 후 (root.lt.lt->root.lt.rt, 여기서 root.lt는 매개변수 root로 다시 받음)
//(2) 모든 로직이 돌면 rt 수행 (root.rt.lt->root.rt.rt, 여기서 root.rt는 매개변수 root로 다시 받음)
DFS(root.lt);
System.out.print(root.data+" ");
DFS(root.rt);
}
}
public static void main(String args[]) {
ExampleFive T = new ExampleFive();
//객체가 생성되는 순간 rt와 lt의 주소값은 null, data는 생성자의 매개변수로 인해 1로 세팅됨
T.root = new Node(1);
//root객체의 lt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 2로 세팅
T.root.lt = new Node(2);
//root객체의 rt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 3로 세팅
T.root.rt = new Node(3);
//.. 꼬리를 물며 반복, 이때부터 생성되는 객체의 주소값은 null
T.root.lt.lt = new Node(4);
T.root.lt.rt = new Node(5);
T.root.rt.lt = new Node(6);
T.root.rt.rt = new Node(7);
//T.root는 그림과 같은 100번지 주소
T.DFS(T.root);
}
}
후위순회 코드
package section7;
class Node{
int data;
//인스턴스 변수 lt, rt는 Node라는 객체 주소를 저장
Node lt, rt;
public Node(int val) {
data = val;
lt = rt = null;
}
}
//이진트리 순회(깊이우선탐색)
public class ExampleFive {
Node root;
// 들어온 매개변수 root는 100번지
public void DFS(Node root) {
//root가 null이면 말단 노드로 온 것
if(root==null) return;
else {
//root 노드에서는 lt와 rt 모두 뻗어 가야됨
/**
* 후위순회
*/
//(1) lt 먼저 수행한 후 (root.lt.lt->root.lt.rt, 여기서 root.lt는 매개변수 root로 다시 받음)
//(2) 모든 로직이 돌면 rt 수행 (root.rt.lt->root.rt.rt, 여기서 root.rt는 매개변수 root로 다시 받음)
DFS(root.lt);
DFS(root.rt);
System.out.print(root.data+" ");
}
}
public static void main(String args[]) {
ExampleFive T = new ExampleFive();
//객체가 생성되는 순간 rt와 lt의 주소값은 null, data는 생성자의 매개변수로 인해 1로 세팅됨
T.root = new Node(1);
//root객체의 lt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 2로 세팅
T.root.lt = new Node(2);
//root객체의 rt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 3로 세팅
T.root.rt = new Node(3);
//.. 꼬리를 물며 반복, 이때부터 생성되는 객체의 주소값은 null
T.root.lt.lt = new Node(4);
T.root.lt.rt = new Node(5);
T.root.rt.lt = new Node(6);
T.root.rt.rt = new Node(7);
//T.root는 그림과 같은 100번지 주소
T.DFS(T.root);
}
}
06. 부분집합 구하기(DFS)
설명
자연수 N이 주어지면 1부터 N까지의 원소를 갖는 집합의 부분집합을 모두 출력하는 프로그램을 작성하세요.
입력
첫 번째 줄에 자연수 N(1<=N<=10)이 주어집니다.
출력
첫 번째 줄부터 각 줄에 하나씩 부분집합을 아래와 출력예제와 같은 순서로 출력한다.
단 공집합은 출력하지 않습니다.
예시 입력 1
3
예시 출력 1
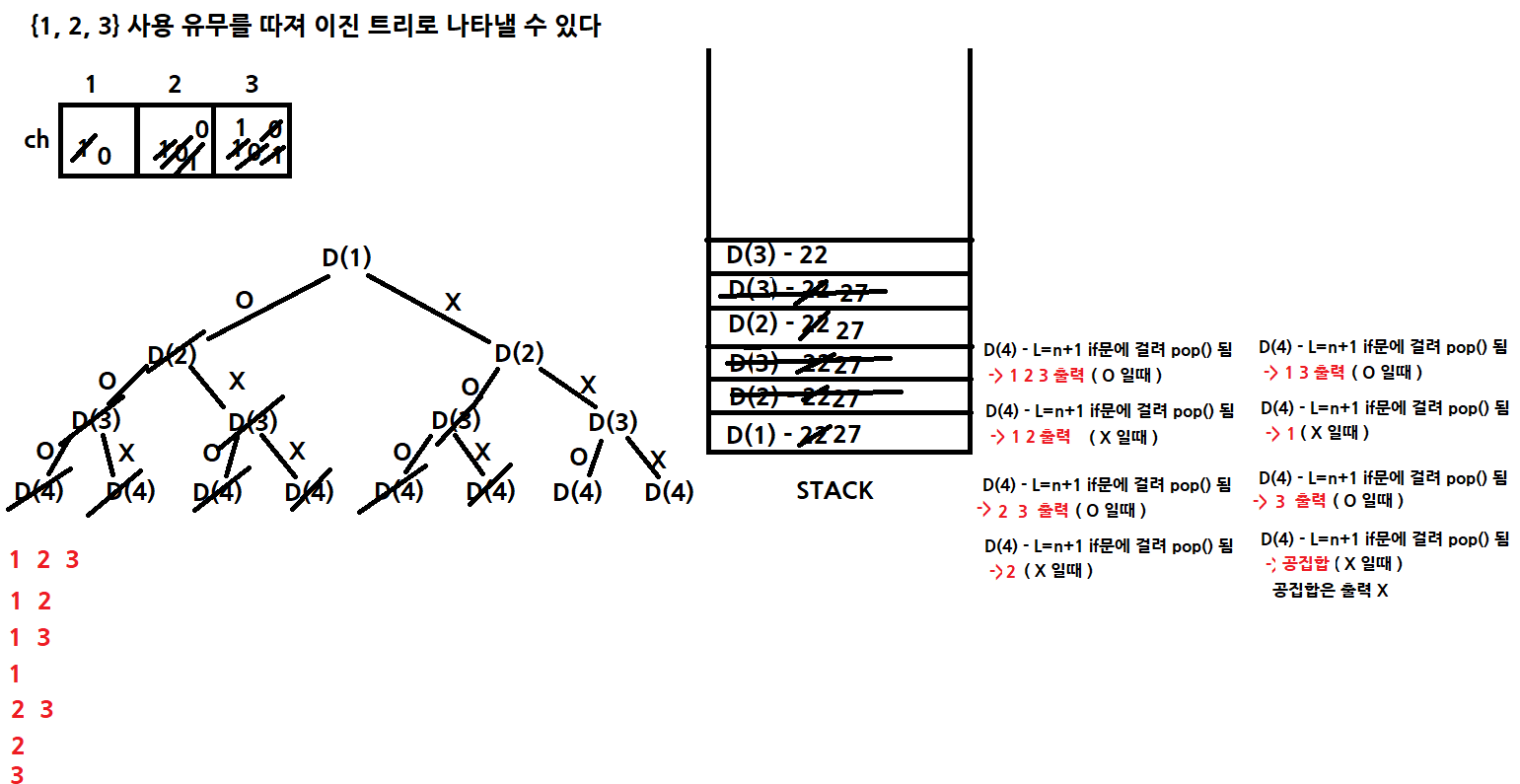
1 2 3
1 2
1 3
1
2 3
2
3
코드
package section7;
//부분집합 구하기(DFS)
public class ExampleSix {
//집합의 원소의 개수
static int n;
//체크배열: 부분집합 사용 여부 체크
static int[] ch;
public void DFS(int L) {
//if는 종착점
if (L == n + 1) {
String tmp = "";
for (int i = 1; i <= n; i++) {
if(ch[i] == 1) tmp += (i + " ");
}
if (tmp.length() > 0) System.out.println(tmp);
} else {
//사용 = 1
ch[L] = 1;
//왼쪽으로 뻗기
DFS(L + 1);
//사용 X = 0
ch[L] = 0;
//오른쪽으로 뻗기
DFS(L + 1);
}
}
public static void main(String[] args) {
ExampleSix T = new ExampleSix();
n = 3;
ch = new int[n + 1];
T.DFS(1);
}
}
07. 이진트리 순회(넓이우선탐색 : 레벨탐색)
설명
아래 그림과 같은 이진트리를 레벨탐색 연습하세요.
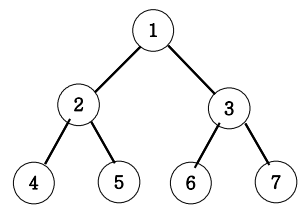
레벨 탐색 순회 출력 : 1 2 3 4 5 6 7
추가설명
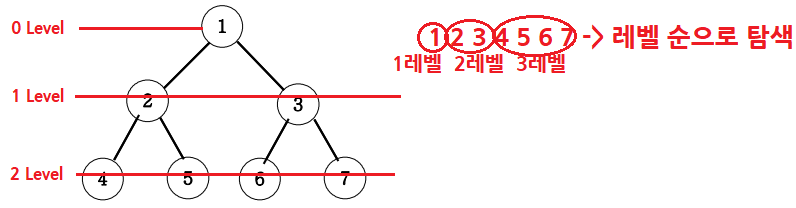

< main 부분 >
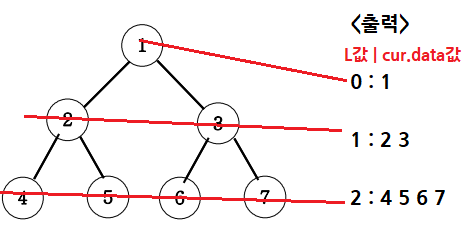
코드
//이진트리 순회(깊이우선탐색)
import java.util.LinkedList;
import java.util.Queue;
class Node2{
int data;
//인스턴스 변수 lt, rt는 Node라는 객체 주소를 저장
Node2 lt, rt;
public Node2(int val) {
data = val;
lt = rt = null;
}
}
public class Main {
Node2 root;
// 들어온 매개변수 root는 100번지
public void BFS(Node2 root) {
Queue<Node2> Q = new LinkedList<>();
Q.offer(root);
//L : 레벨
int L = 0;
while (!Q.isEmpty()) {
//해당 레벨의 Q의 사이즈
int len = Q.size();
System.out.print(L+ " : " );
for (int i = 0; i < len; i++) {
//Q에 가장 먼저 추가된 Node2부터 cur이라는 변수에 대입 후 삭제
Node2 cur = Q.poll();
System.out.print(cur.data + " ");
//상위노드의 lt가 존재하면 Q에 추가
if(cur.lt!=null) Q.offer(cur.lt);
//상위노드의 rt가 존재하면 Q에 추가
if(cur.rt!=null) Q.offer(cur.rt);
}
//다음 레벨 +1
L++;
System.out.println();
}
}
public static void main(String args[]) {
Main T = new Main();
//객체가 생성되는 순간 rt와 lt의 주소값은 null, data는 생성자의 매개변수로 인해 1로 세팅됨
T.root = new Node2(1);
//root객체의 lt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 2로 세팅
T.root.lt = new Node2(2);
//root객체의 rt의 주소값이 생기면서, 주소를 가르치는 객체의 data는 3로 세팅
T.root.rt = new Node2(3);
//.. 꼬리를 물며 반복, 이때부터 생성되는 객체의 주소값은 null
T.root.lt.lt = new Node2(4);
T.root.lt.rt = new Node2(5);
T.root.rt.lt = new Node2(6);
T.root.rt.rt = new Node2(7);
//T.root는 그림과 같은 100번지 주소
T.BFS(T.root);
}
}
08. 송아지 찾기 1(BFS : 상태트리탐색)
설명
현수는 송아지를 잃어버렸다. 다행히 송아지에는 위치추적기가 달려 있다.
현수의 위치와 송아지의 위치가 수직선상의 좌표 점으로 주어지면 현수는 현재 위치에서 송아지의 위치까지 다음과 같은 방법으로 이동한다.
송아지는 움직이지 않고 제자리에 있다.
현수는 스카이 콩콩을 타고 가는데 한 번의 점프로 앞으로 1, 뒤로 1, 앞으로 5를 이동할 수 있다.
최소 몇 번의 점프로 현수가 송아지의 위치까지 갈 수 있는지 구하는 프로그램을 작성하세요.
입력
첫 번째 줄에 현수의 위치 S와 송아지의 위치 E가 주어진다. 직선의 좌표 점은 1부터 10,000까지이다.
출력
점프의 최소횟수를 구한다. 답은 1이상이며 반드시 존재합니다.
예시 입력 1
5 14
예시 출력
3
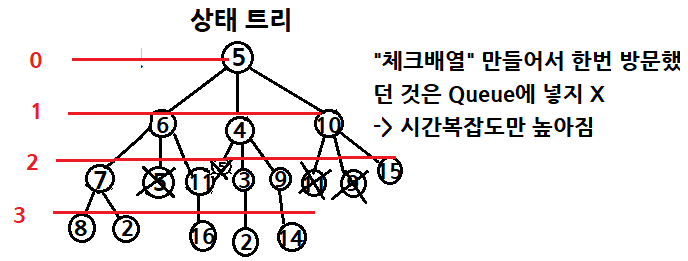
코드
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
//송아지 찾기 1(BFS : 상태트리탐색)
public class Main {
//점프의 최소횟수
int answer = 0;
//한번 점프할 때 갈 수 있는 거리
int[] dis = {1, -1, 5};
//체크배열 생성
int[] check;
Queue<Integer> Q = new LinkedList<>();
public int DFS(int s, int e) {
//직선의 좌표 점은 1~10,000까지
check = new int[10001];
//출발지점 설정
check[s] = 1;
//출발지점 Q에 대입
Q.offer(s);
//L : level
int L = 0;
while (!Q.isEmpty()) {
//각 레벨에 있는 원소의 개수
int len = Q.size();
for (int i = 0; i < len; i++) {
//해당 레벨에 Queue에서 꺼내 반환(삭제)
int x = Q.poll();
//원소 1개 당 dis인 1, -1, 5 이동하여 각 상황 비교
for (int j = 0; j < 3; j++) {
//1, -1, 5씩 이동하여 nx 변수에 대입
int nx = x + dis[j];
//x(=송아지 위치)와 nx(=x에서 이동한 값)가 동일하면 L+1(=level+1) 리턴 -> Queue에 넣고 비교하는 것보다, 넣기 전에 비교하는게 훨씬 효율적
if(nx == e) return L+1;
//nx가 방문하지 않은 노드라면 (1~10,000 사이 좌표, check 배열에 해당 인덱스가 0인 숫자)
if (nx >= 1 && nx <= 10000 && check[nx] == 0) {
check[nx] = 1;
Q.offer(nx);
}
}
}
//level +1
L++;
}
return answer;
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
int s = kb.nextInt();
int e = kb.nextInt();
System.out.println(T.DFS(s, e));
}
}09. Tree 말단 노드까지의 가장 짧은 경로 - DFS 풀이(사실 최단거리일 때는 BFS로 풀어야 함)
설명
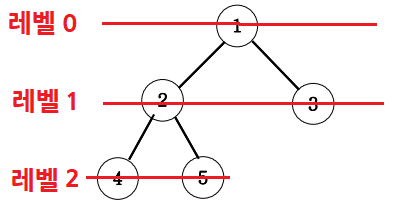
아래 그림과 같은 이진트리에서 루트 노드 1에서 말단노드까지의 길이 중 가장 짧은 길이를 구하는 프로그램을 작성하세요.
각 경로의 길이는 루트노드에서 말단노드까지 가는데 이동하는 횟수를 즉 간선(에지)의 개수를 길이로 하겠습니다.

가장 짧은 길이는 3번 노느까지의 길이인 1이다.
추가설명
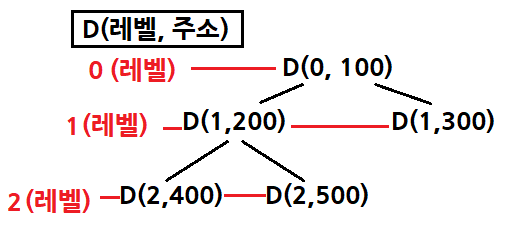
코드
//Tree 말단 노드까지의 가장 짧은 경로
class Node3 {
int data;
Node3 lt, rt;
Node3(int val) {
data = val;
lt = rt = null;
}
}
public class Main {
Node3 root;
public int DFS(int L, Node3 root) {
//상위노드의 lt rt 값이 null이라면(Node3 객체가 없다면 = 주소가 null이라면) 매개변수로 받은 레벨값 리턴
if(root.lt == null && root.rt == null) return L;
//상위노드에서 lt rt 값 중 작은 값을 리턴, 그냥 리턴이 아니라 DFS에 넣어 리턴하여 "재귀함수" 구현
else return Math.min(DFS(L + 1, root.lt), DFS(L + 1, root.rt));
}
public static void main(String[] args) {
Main T = new Main();
T.root = new Node3(1);
T.root.lt = new Node3(2);
T.root.rt = new Node3(3);
T.root.lt.lt = new Node3(4);
T.root.lt.rt = new Node3(5);
//0번 레벨과, 이진트리의 맨 위에 있는 root(Node3 객체 통째로 넣기 때문에 주소값)를 매개변수로 넣음
System.out.println(T.DFS(0, T.root));
}
}
10. Tree 말단 노드까지의 가장 짧은 경로 - BFS 풀이
설명
아래 그림과 같은 이진트리에서 루트 노드 1에서 말단노드까지의 길이 중 가장 짧은 길이를 구하는 프로그램을 작성하세요.
각 경로의 길이는 루트노드에서 말단노드까지 가는데 이동하는 횟수를 즉 간선(에지)의 개수를 길이로 하겠습니다.

가장 짧은 길이는 3번 노느까지의 길이인 1이다.
코드
import java.util.LinkedList;
import java.util.Queue;
//Tree 말단 노드까지의 가장 짧은 경로 - BFS
class Node4 {
int data;
Node4 lt, rt;
Node4(int val) {
data = val;
lt = rt = null;
}
}
public class Main {
Node4 root;
public int BFS(Node4 root) {
Queue<Node4> Q = new LinkedList<>();
//이진트리의 상위 노드 값 Queue에 저장
Q.offer(root);
//레벨 0 설정
int L = 0;
//Queue가 비어있지 않다면
while (!Q.isEmpty()) {
//Queue의 size를 len에 대입 후
int len = Q.size();
//len 길이만큼 for문이 돌아감
for (int i = 0; i < len; i++) {
//Queue에 넣었던 노드 값을 cur에 대입하면서 Queue에서 삭제
Node4 cur = Q.poll();
//cur의 lt(왼쪽)에 위치한 노드가 null, cur의 lt(오른쪽)에 위치한 노드가 null 이라면 레벨 리턴 후 출력
if (cur.lt == null && cur.rt == null) return L;
// cur의 lt(왼쪽)에 위치한 노드가 null이 아니라면 Queue에 해당 노드 저장
if (cur.lt != null) Q.offer(cur.lt);
// cur의 lt(오른쪽)에 위치한 노드가 null이 아니라면 Queue에 해당 노드 저장
if (cur.rt != null) Q.offer(cur.rt);
}
//레벨+1
L++;
}
//실제로 여기까진 오지 않지만 에러가 발생하므로, while문이 돌지 않았을 때를 가정하여 0으로 리턴
return 0;
}
public static void main(String[] args) {
Main T = new Main();
T.root = new Node4(1);
T.root.lt = new Node4(2);
T.root.rt = new Node4(4);
T.root.lt.lt = new Node4(4);
T.root.lt.rt = new Node4(5);
//0번 레벨과, 이진트리의 맨 위에 있는 root(Node4 객체 통째로 넣기 때문에 주소값)를 매개변수로 넣음
System.out.println(T.BFS(T.root));
}
}
11. 그래프와 인정행렬
그래프를 기호로 G(V,E) 라고 한다
- V: 노드(=정점)
- E: 노드와 노드를 연결하는 간선
-> 그래프는 vertex(V)와 edge(E)로 이루어진 집합
1. 무방향 그래프
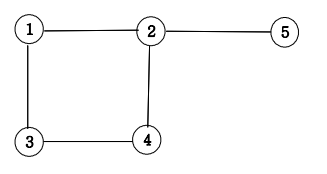
무방향 그래프가 입력으로 들어오면 어떻게 되는가?
1 2
1 3
2 4
3 4
2 5
-> 정점의 개수: 5, 간선의 개수: 5그렇다면 그래프는 어떻게 표현하는가?
이러한 인접행렬은2차원 배열로 표현한다.
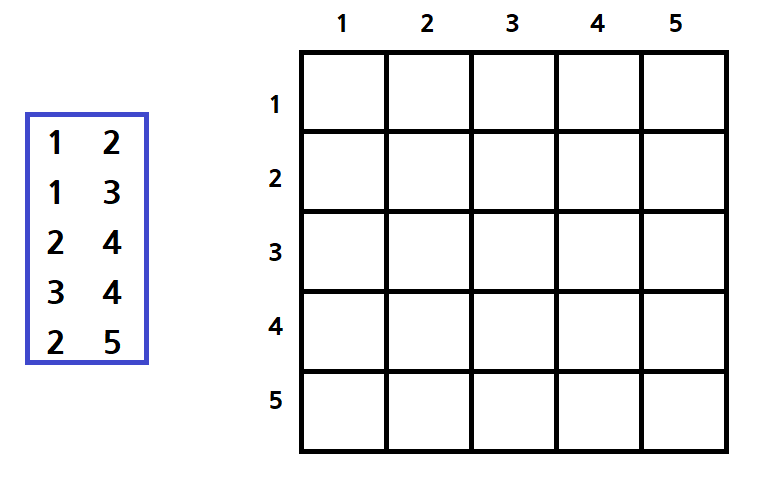
2차원 배열과 입력 데이터가 있다.
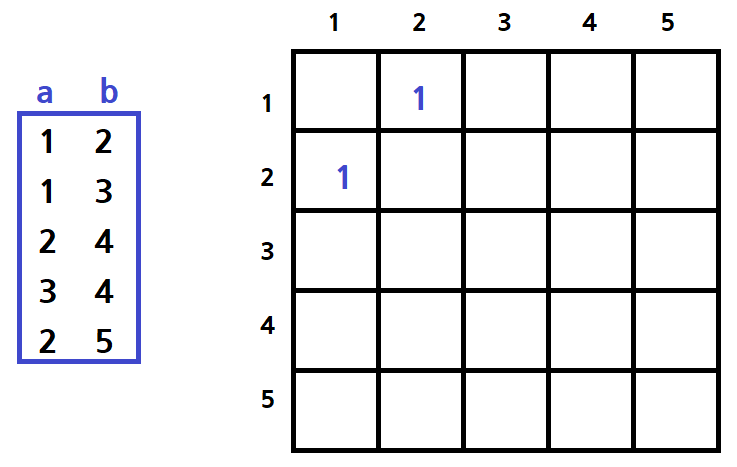
2차원 배열에 첫 번째 줄에 있는 1, 2 간선정보가 들어오면 1번 노드와 2번 노드가 연결된 간선이 있구나 라고 생각하며 1행 2열, 2행 1열을 체크한다.
만약 node인 왼쪽 데이터를 a로 읽고, 오른쪽 데이터를 b로 읽었다면
graph[a][b]=1;
graph[b][a]=1;라고 표현할 수 있다.
나머지 데이터로 그래프에 표시해보자. 빈칸은 0으로 채운다.
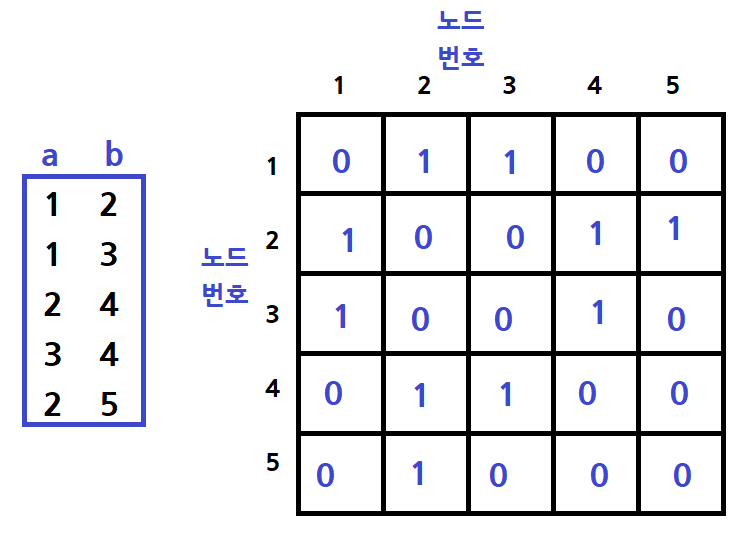
이것을 가지고 행번호를 탐색할 수 있다.
행에 오는 값을 기준으로 생각해보면 다음과 같다.
1행 즉, 1번 정점과 연결된 정점이 누구인가 했을 때 1행 N열에 값이 1인 N열이 1번 정점과 연결된 정점이다.
따라서 1행 2열, 1행 3열에 값이 1이므로 2번 정점과 3번 정점이 1번 정점과 연결된 정점이다.
2번 정점과 연결된 정점 또한 2행 4열, 2행 5열에 값이 1이 있으므로 4번 정점 5번 정점과 연결되어 있음을 알 수 있다.
2. 방향 그래프
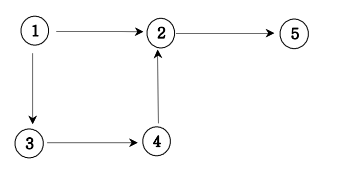
방향 그래프 = 이동하는 방향이 정해져 있는 그래프
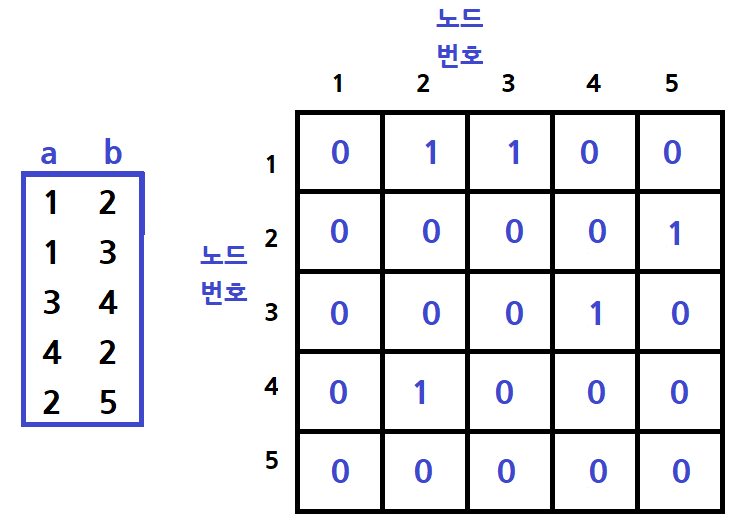
만약 node인 왼쪽 데이터를 a로 읽고, 오른쪽 데이터를 b로 읽었다면
graph[a][b]=1;라고 표현할 수 있다. 방향그래프는 바꿔치기 하지 않고 한 번만 표현한다.
"행번호에서 열번호로 이동한다" 고 해석한다.
행에 오는 값을 기준으로 생각해보면 다음과 같다.
만약 3번 노드에서 갈 수 있는 노드가 무엇인지 볼 때 3행에 고정을 해놓고 3행 N열에 값이 1인 N열이 3번 노드와 연결된 노드이다.
따라서 3행 4열이 값이 1이므로 4번 노드가 연결된 노드이다.
3. 가중치 방향 그래프
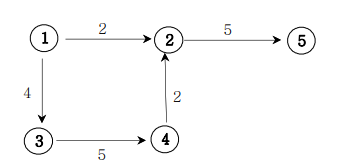
방향 그래프와 간선에 가중치 값 까지 있는 그래프를 가중치 방향 그래프라고 한다.
1번 노드에서 2번 노드로 이동하는데 비용이 2이다.
(ex > 1번 도시에서 2번 도시로 물류를 이동할 때 비용이 2)
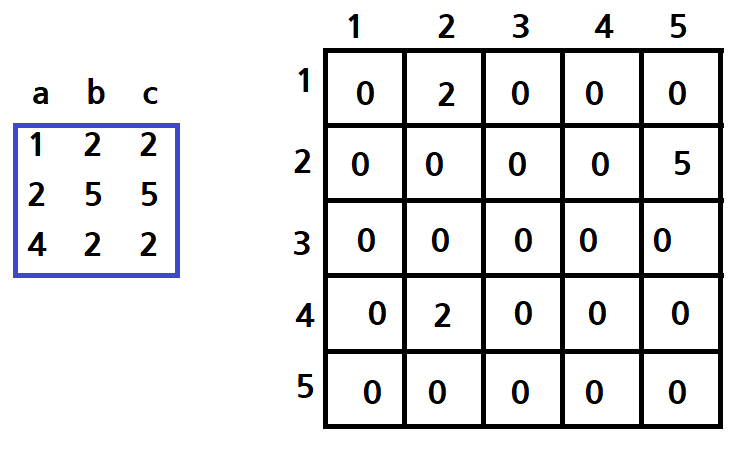
만약 node인 왼쪽 데이터를 a로 읽고, 오른쪽 데이터를 b로 읽었다면
graph[a][b]=c;라고 표현할 수 있다. 가중치 값 c는 결과 값이다.
12. 경로 탐색(인접행렬)
설명
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요.
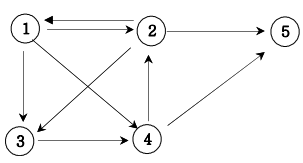
위 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는
1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 6가지 이다.
입력
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다.
출력
총 가지수를 출력한다.
예시 입력 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
예시 출력 1
6
코드
import java.util.Scanner;
//경로 탐색(인접행렬)
public class Main {
static int n,m, answer = 0;
static int[][] graph;
static int[] ch;
public void DFS(int v) {
//5번 노드에 도달했을때 answer를 1 증가
if(v==n) answer++;
else{
// 행은 v로 고정하고, 열은 1~5가 돌아가며 for문
for (int i = 1; i <= n; i++) {
// 해당 노드가 1이고, ch(=check)배열 값이 0이라면
if (graph[v][i] == 1 && ch[i] == 0) {
//ch[i] 값을 1로 변경
ch[i] = 1;
//재귀함수 동작, graph 배열의 행을 i로 하여 반복
DFS(i);
//DFS가 Stack 형태에서 하나씩 꺼내질 때 (되돌아갈 때 = 5번 노드에 도달했을 때) ch(=check)는 1에서 0으로 바꿔줘야 함
//그래야 다른 경우의 수도 셀 수 있음
ch[i] = 0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
n = kb.nextInt();
m = kb.nextInt();
//이차원 배열, 인접행렬
graph = new int[n+1][n+1];
ch = new int[n + 1];
for (int i = 0; i < m; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
//입력한 노드의 값은 1
graph[a][b] = 1;
}
//1에서 출발 시 ch[1]을 1로 세팅 (1행1열에서 출발해서)
ch[1] = 1;
//DFS 시작
T.DFS(1);
//5번 노드에 도달한 경우의 수
System.out.println(answer);
}
}
13. 경로 탐색(인접리스트)
13번 문제는 12번 문제와 동일하나 인접리스트로 풀어보려고 한다.
설명
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요.

위 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는
1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 6가지 이다.
입력
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다.
출력
총 가지수를 출력한다.
예시 입력 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
예시 출력 1
6
인접리스트는 언제 사용?
만약 정점이 1000개, 10,000개 이런 식으로 들어오게 되면 인접행렬 은 너무 비효율적이다.
인접행렬은 정점이 5개라고 하면 5행 5열로 배열을 만들면 된다.
하지만 1000개라고 하면 1000행 1000열로 만들어 행마다 열을 탐색하며 for문이 돌게되면 시간복잡도로도 비효율적이고 엄청나게 메모리를 크게 잡게 된다.이럴 때 인접리스트가 필요하다.
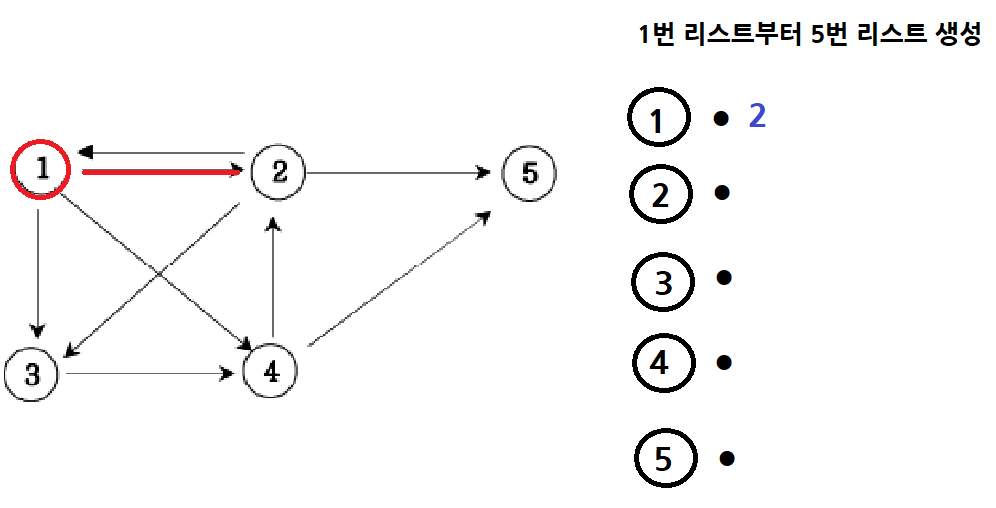
ArrayList 객체가 1번 객체부터 5번 객체까지 있다.
간선 정보가 1, 2가 들어오면 1번 ArrayList에 2를 추가한다.
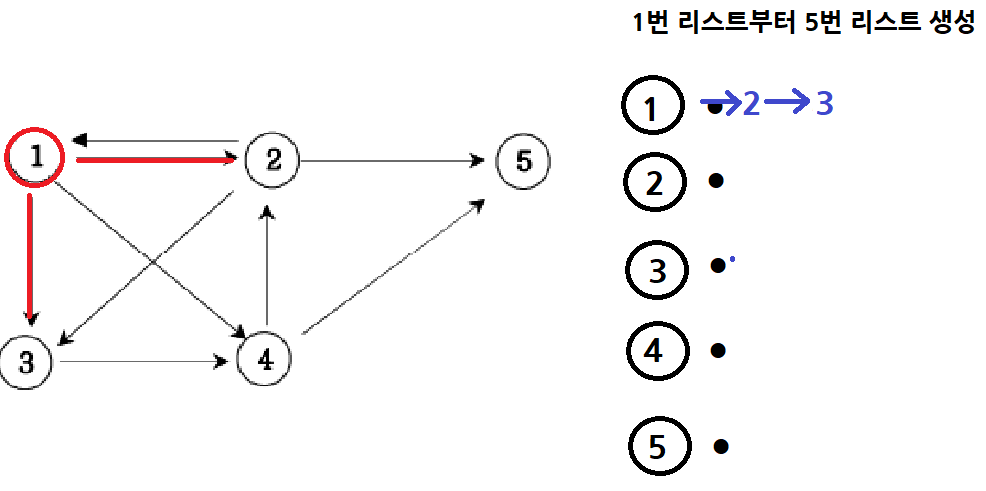
그 다음에 간선 정보가 1, 3이 들어오면 1번 ArrayList에 3를 추가한다.
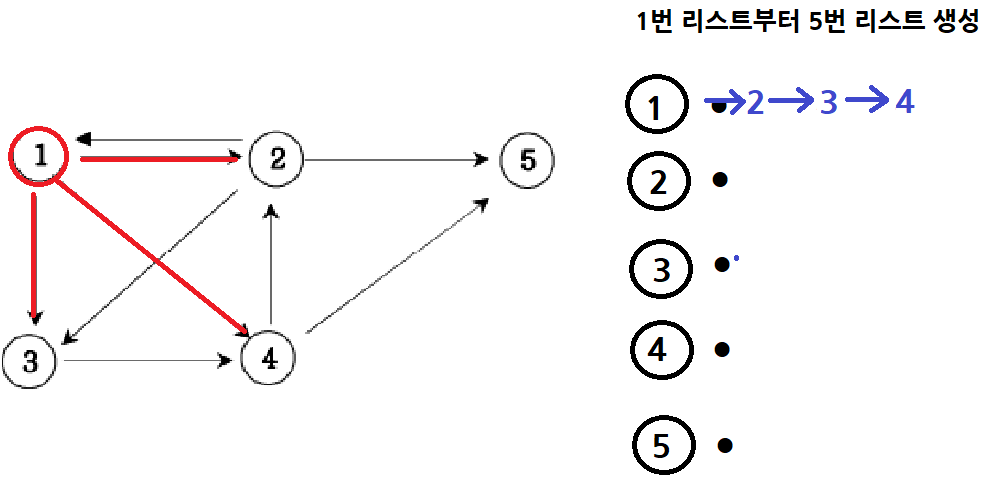
그 다음에 간선 정보가 1, 4이 들어오면 1번 ArrayList에 4를 추가한다.

그 다음에 간선 정보가 1, 5이 들어오면 1번 ArrayList에 5를 추가한다.
그 다음에 간선 정보가 2, 1이 들어오면 2번 ArrayList에 1를 추가한다.
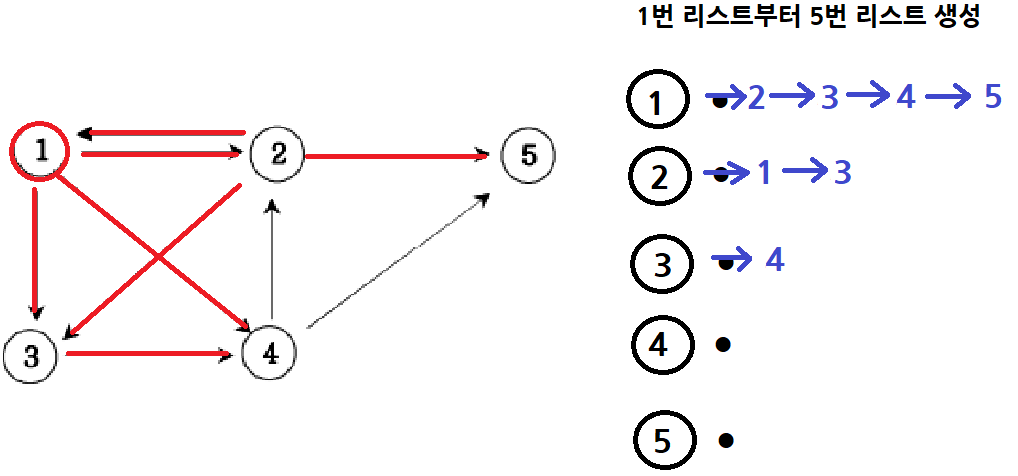
그 다음에 간선 정보가 2, 3이 들어오면 2번 ArrayList에 3를 추가한다.
그 다음에 간선 정보가 3, 4이 들어오면 3번 ArrayList에 4를 추가한다.
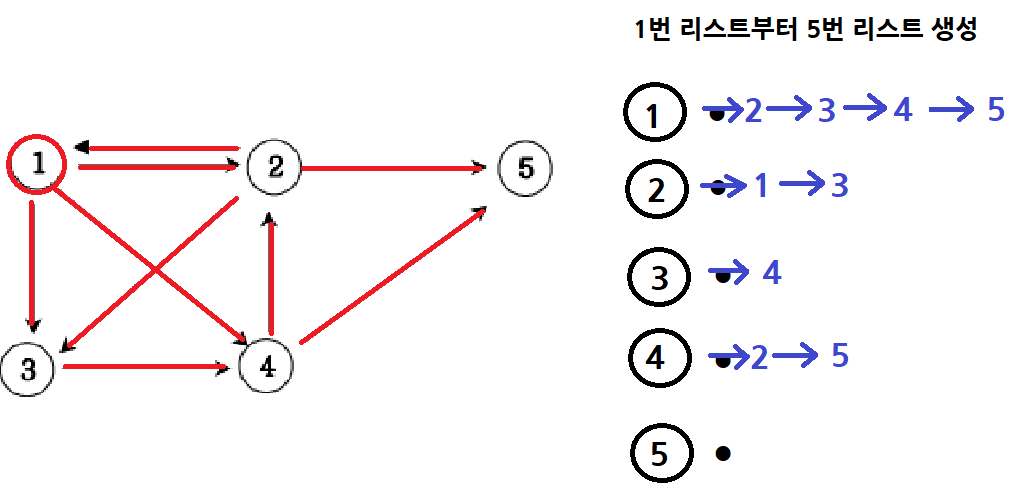
그 다음에 간선 정보가 4, 2이 들어오면 4번 ArrayList에 2를 추가한다.그 다음에 간선 정보가 4, 5이 들어오면 4번 ArrayList에 5를 추가한다.
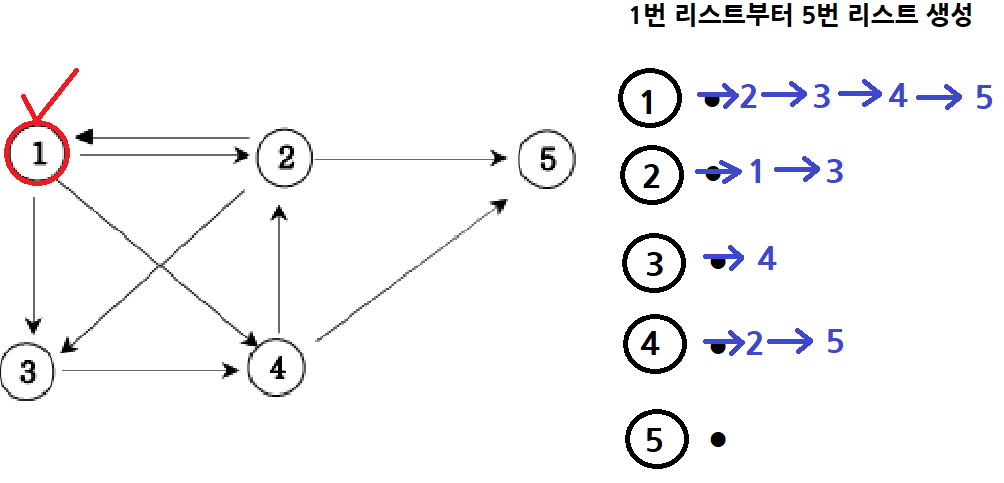
이런식으로 각 노드의 ArrayList를 간선 정보를 토대로 추가한 뒤, 1번 정점에서 출발하여 탐색을 시작한다.
이는 인접행렬 때처럼 정점이 10,000개여도 1부터 10,000개까지 돌 필요 없이 ArrayList만 탐색해도 된다.
코드
import java.util.ArrayList;
import java.util.Scanner;
//경로 탐색(인접리스트)
public class Main {
static int n,m, answer = 0;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch;
public void DFS(int v) {
if(v==n) answer++;
else{
//v 정점에 갈 수 있는 것은 v번 ArrayList에 추가되어 있음
for (int nv : graph.get(v)) {
// v번 ArrayList에 저장되어 있는 것(nv)들 중 체크배열(ch[nv])이 0 이라면
if (ch[nv] == 0) {
//체크배열(ch[nv])를 1로 만들고
ch[nv] = 1;
//nv번 ArrayList를 찾아 재귀함수 출동
DFS(nv);
//되돌아갈 때 (= 5번 노드에 도달했을 때) ch[nv]는 1에서 0으로 바꿔줘야 함
ch[nv] = 0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
n = kb.nextInt();
m = kb.nextInt();
//ArrayList Integer를 저장할 수 있는 ArrayList 객체를 저장하는 ArrayList
graph = new ArrayList<ArrayList<Integer>>();
//정수를 저장할 수 있는 1번부터 n번까지 ArrayList 객체가 있어야 된다. (0번은 무의미함, 버리는 숫자)
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<Integer>());
}
ch = new int[n + 1];
for (int i = 0; i < m; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
//a번 ArrayList에 접근, a번 ArrayList에 b를 추가
//ex> 3번 노드 ArrayList에 5번 노드 추가 (3->5)
graph.get(a).add(b);
}
ch[1] = 1;
//DFS 시작
T.DFS(1);
//5번 노드에 도달한 경우의 수
System.out.println(answer);
}
}
14. 그래프 최단거리(BFS)
설명
다음 그래프에서 1번 정점에서 각 정점으로 가는 최소 이동 간선수를 출력하세요.
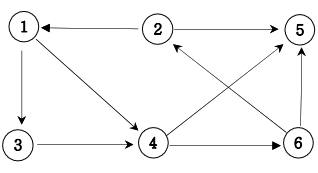
입력
첫째 줄에는 정점의 수 N(1<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연결정보가 주어진다.
출력
1번 정점에서 각 정점으로 가는 최소 간선수를 2번 정점부터 차례대로 출력하세요.
예시 입력 1
6 9
1 3
1 4
2 1
2 5
3 4
4 5
4 6
6 2
6 5
예시 출력 1
2 : 3
3 : 1
4 : 1
5 : 2
6 : 2
2가지 방법이 있다
1) BFS를 레벨로 탐색 2) BFS를 거리로 탐색
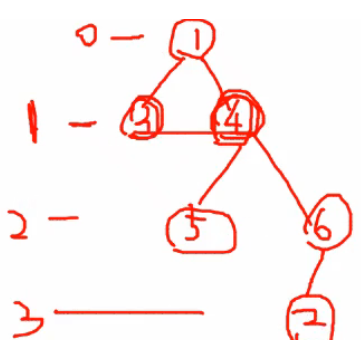
< BFS를 레벨로 탐색 >
1번 방법도 있지만 2번 방법으로 풀어 보았다.
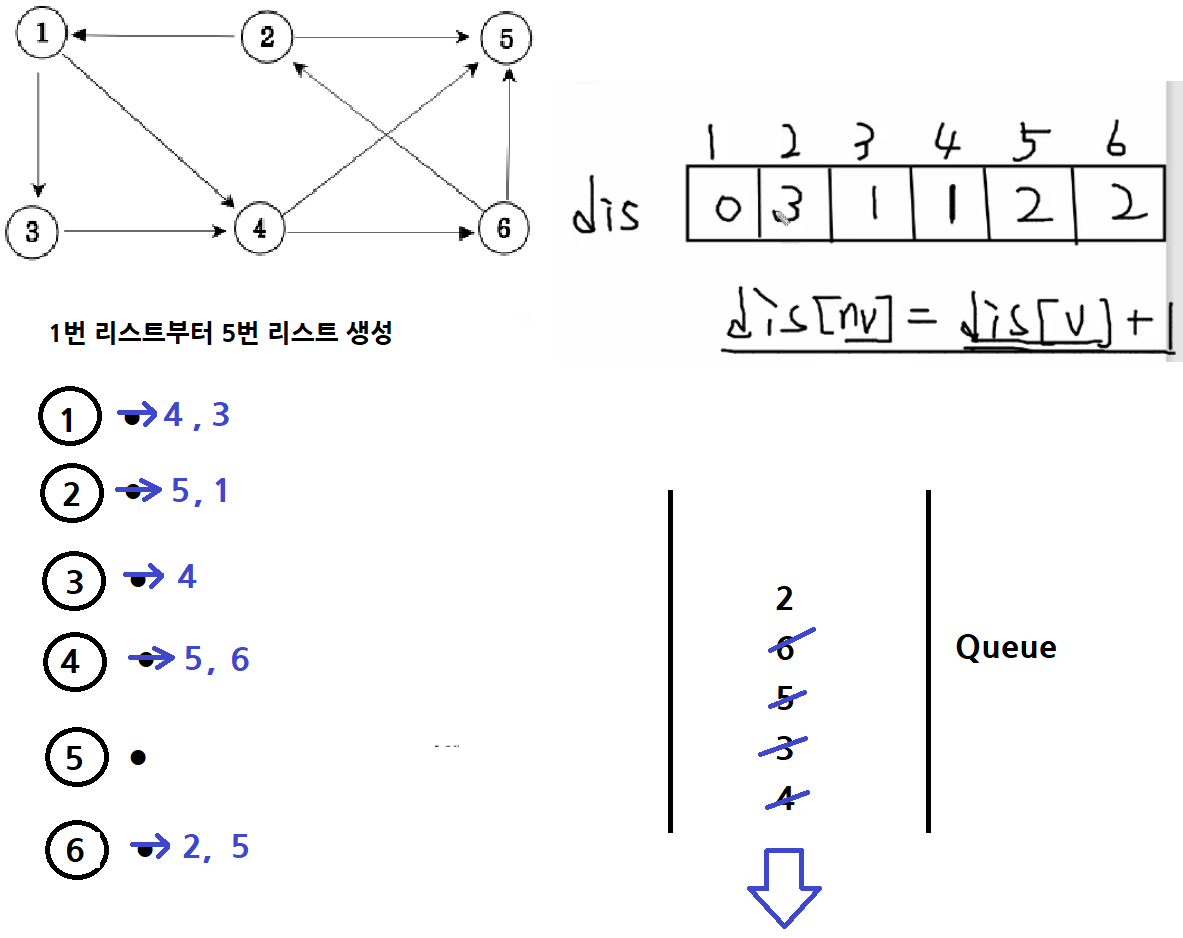
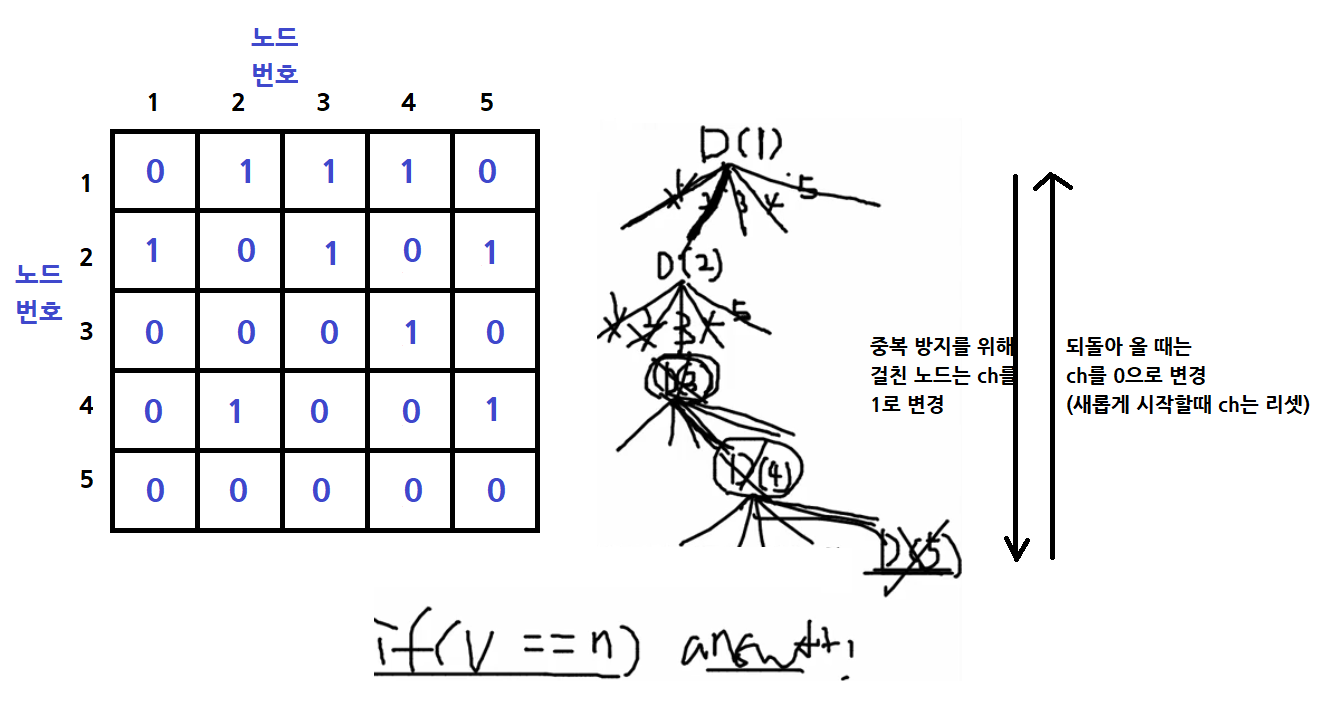
노드 1과의 최소 거리를 Queue와 check 배열을 통해 계산할 수 있다.
처음 만난 노드라면 check[노드]를 0에서 1로 변경해주고, Queue에 넣어준 뒤 이전 노드에서 현재 노드까지의 거리+1 하여 최소 간선수를 구한다.
현재 노드에서 다른 노드로 출발할 때 check[다른 노드]가 1이면 현재 노드에서 구했던 간선수가 최소 간선수 이고, check[다른 노드]가 0이면 위 로직을 반복한다.
코드
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
//그래프 최단거리(BFS)
public class Main {
static int n, m;
static ArrayList<ArrayList<Integer>> graph;
static int[] ch, dis;
static void BFS(int v) {
Queue<Integer> Q = new LinkedList<>();
//Queue에 1 추가
Q.offer(v);
while (!Q.isEmpty()) {
//Queue에 있는 요소를 꺼내면서 (삭제하면서) cv에 대입
int cv = Q.poll();
for (int nv : graph.get(cv)) {
//check 배열이 0이라면 (최초방문)
if (ch[nv] == 0) {
//방문했으니 check 배열은 1로 변경
ch[nv] = 1;
//Queue에 nv 추가
Q.offer(nv);
//노드 nv는 노드 cv에서 + 1 만큼의 거리
dis[nv] = dis[cv] + 1;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner kb = new Scanner(System.in);
//정점의 개수
n = kb.nextInt();
//간선의 개수
m = kb.nextInt();
//인접리스트 공간 확보
graph = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<Integer>());
}
//체크배열
ch = new int[n + 1];
//거리배열
dis = new int[n + 1];
//인접리스트 값 대입
for (int i = 0; i < m; i++) {
int a = kb.nextInt();
int b = kb.nextInt();
graph.get(a).add(b);
}
ch[1] = 1;
dis[1] = 0;
//BFS 시작 (너비우선탐색)
T.BFS(1);
for (int i = 2; i <= n; i++) {
System.out.println(i + " : " + dis[i]);
}
}
}
