
DB의 인덱스에 대한 개념을 찾다가 정리한 글이다.
결론을 말하자면 인덱스는 B+TREE 방식이 사용된다.
B-TREE와 B+TREE는 어떤 차이가 있고, 왜 DB 인덱스는 B+TREE가 쓰이는지 알아보자.
이진 트리
B-TREE를 설명하자고 해놓고, 왜 이진 트리부터 설명하는가.
B-TREE는 결국 이진 트리에서 파생된 자료구조이기 때문에 이진 트리에 대해 정확히 짚고 넘어가려고 한다.
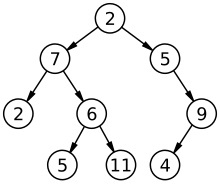
이진 트리는 모든 노드가 최대 2개(0~2)의 하위 노드를 갖는 트리 자료구조이다.
트리의 구성 요소는 다음과 같다.

부모보다 작은 값은 왼쪽, 큰 값은 오른쪽에 저장한다.
데이터가 많아질 수록 비교 횟수가 증가하여 추가, 삭제에 시간이 더 걸린다.
이런 이진 트리에는 몇 가지 종류가 존재한다.
정 이진 트리 (full binary tree)
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
- 중간에 1개의 자식만 가진 노드가 없다.
포화 이진 트리 (perfect binary tree)
- 모든 내부 노드가 정확히 2개의 자식을 가지며, 모든 리프 노드가 같은 레벨에 있다.
- 가장 이상적인 형태이지만, 실제 데이터로 이런 구졸르 만들기 어렵다.
완전 이진 트리 (complete binary tree)
- 마지막 레벨을 제외한 모든 레벨이 채워져 있다.
- 마지막 레벨은 왼쪽부터 차례로 채워진다.
- 힙 자료구조 등에서 사용되며, 효율적인 메모리 사용이 가능하다.
균형 이진 트리 (balanced binary tree)
- 왼쪽과 오른쪽 서브트리의 높이 차이가 최대 1이다.
- 이 구조는 트리의 균형을 유지하여 효율적인 연산을 가능하게 한다.
등등.. 종류가 더 있지만 주요 이진 트리만 가져와봤다.
이 중에 균형 이진 트리가 실제 응용 분야(데이터베이스 인덱싱, 파일 시스템, 네트워크 라우팅 테이블 등)에서 많이 사용된다.
이미 눈치 챈 사람도 있겠지만, 균형 이진 트리의 Balanced의 B를 따서 B-TREE, B+TREE라고 칭하는 것이다.
B-TREE
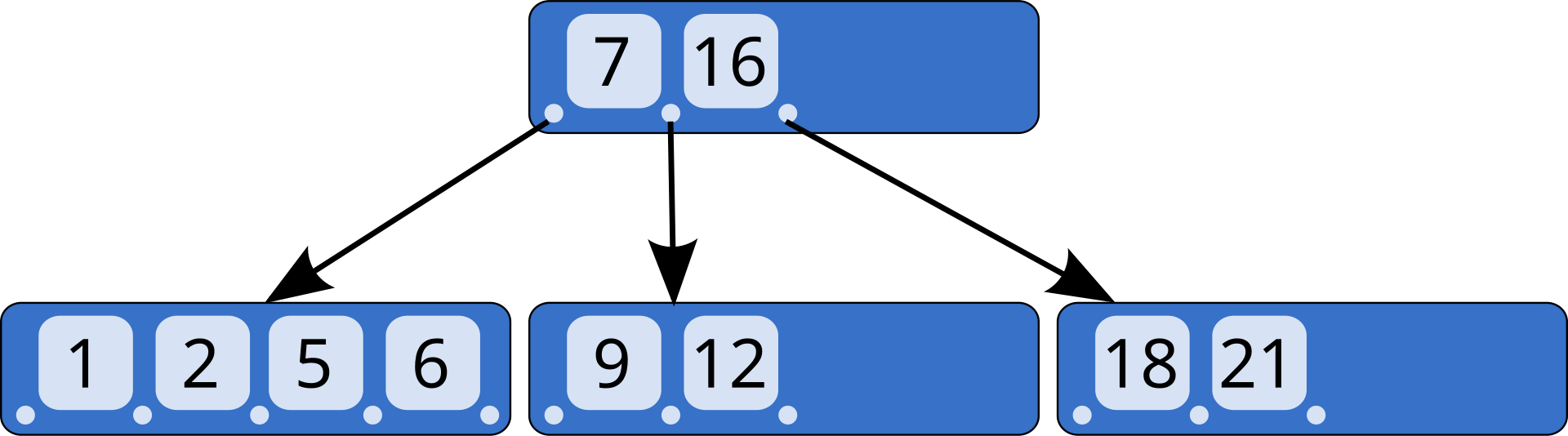
B-TREE는 이진 트리와 다르게 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다.
하나의 노드 최대 자식수가 3개이면 3차 B-TREE, 4개면 4차 B-TREE 라고 한다.
최대 자식수의 개수에 따라서 1,2,3..M차 B-TREE가 있다.
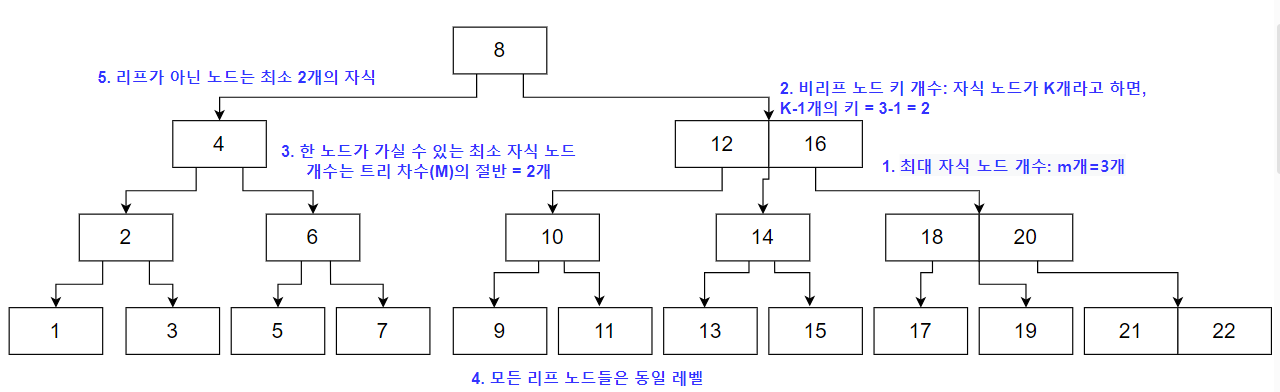
- 최대 자식 노드 개수: B-TREE의 각 노드는 최대 M개의 자식을 가질 수 있다.
- 비리프 노드의 키 개수: 자식 노드가 K개인 비리프 노드는 항상 K-1개의 키를 가지고 있다. 이 키들은 자식 노드들이 저장한 값들을 구간으로 나눠주는 역할을 한다.
- 최소 자식 노드 개수: 모든 내부 노드는 최소 ⌈M/2⌉개의 자식을 가져야 한다. 즉, 한 노드가 가질 수 있는 자식 노드의 개수는 적어도 트리의 차수(M)의 절반이다. (B-트리에서 최소 자식 노드 개수를 결정할 때는
항상 올림을 사용)
- 리프 노드의 동일 레벨: 모든 리프 노드들은 동일한 레벨에 존재해야 한다. 이는 트리가 항상 균형을 유지하도록 보장하여, 트리의 높이가 일정하게 유지되게 한다.
- 리프가 아닌 노드의 최소 자식 수: 리프가 아닌 모든 노드는 최소 2개의 자식을 가져야 한다. 즉, 루트가 아니면서 자식이 없는 노드는 존재할 수 없다.
아래는 3차 트리의 예시를 보여준다.
각 특징을 반영하여 가정할 수 있는 예시이다.
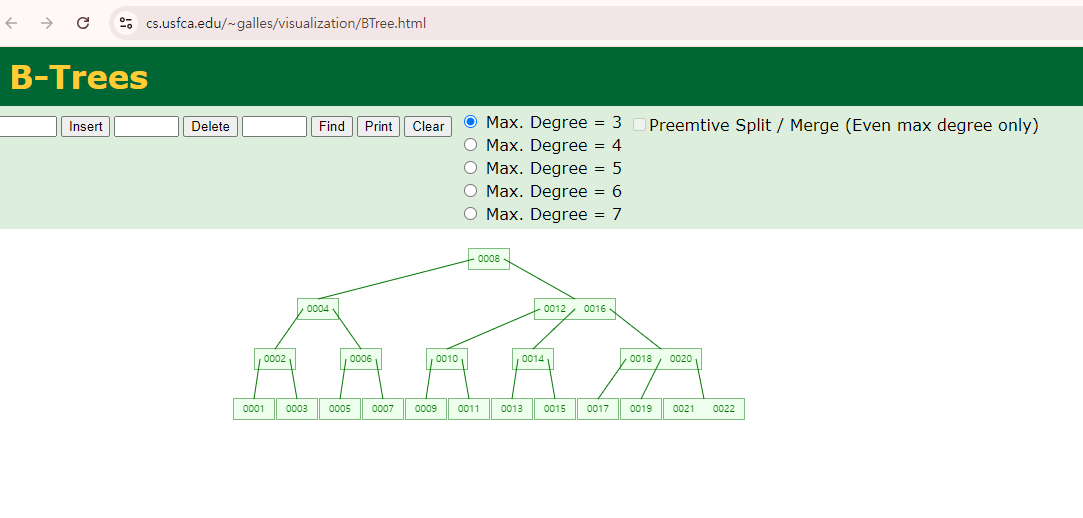
위 링크로 들어가면 B-TREE가 어떻게 구성되는지를 시뮬레이션으로 시각화하여 이해를 돕고 있다.
B+TREE
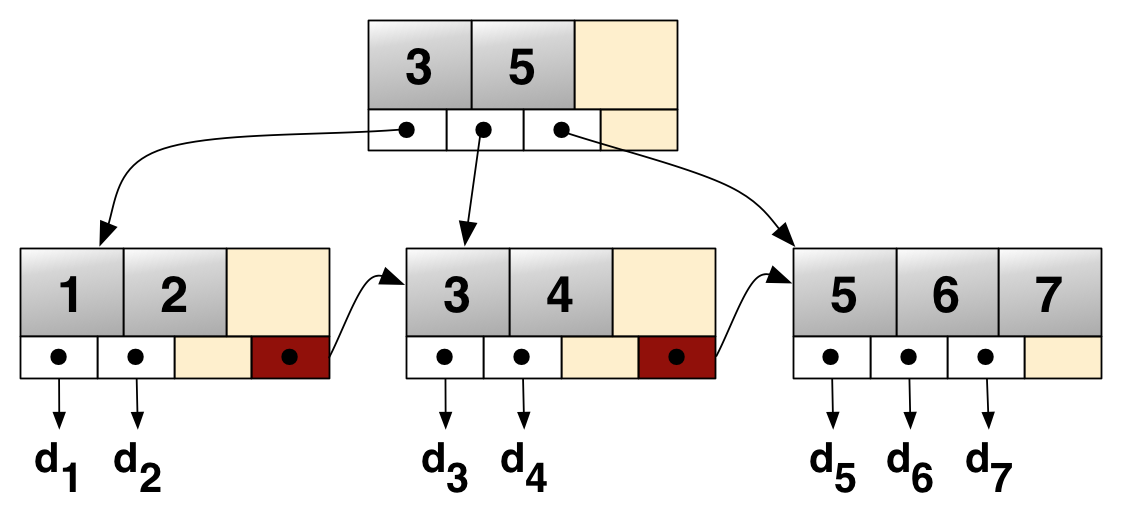
B-TREE는 내부 노드와 리프 노드에 모두 데이터를 저장하는 반면에 B+TREE는 데이터를 리프 노드에만 저장하고, 내부 노드는 오직 키 값만 저장한다.
B+ 트리는 리프 노드가 연결 리스트로 연결되어 있어 순차 검색이 빠르다.
B+ 트리는 리프 노드를 순차적으로 연결하는 포인터 집합을 가지고 있다. 이를 통해 인덱스된 순차 파일을 처리할 때, 포인터를 사용해 키와 값을 일일이 비교하지 않고도 다음 데이터에 빠르게 접근할 수 있어 효율적인 처리가 가능하다.
동일하게 위 링크로 들어가면 B+TREE가 어떻게 구성되는지를 시뮬레이션으로 시각화하여 이해를 돕고 있다.
B-TREE vs B+TREE
시뮬레이션을 통해 B-TREE와 B+TREE가 어떻게 다른지 비교해보자.
1~10까지 숫자를 예제로 비교해보았다.
먼저 B-TREE이다.
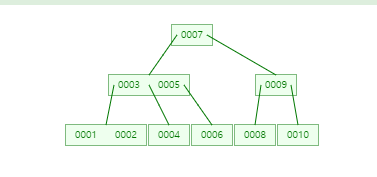
루트 노드 : 7
내부 노드 : 3, 5, 9
리프 노드 : 1, 2, 4, 6, 8, 10
다음은 B+TREE이다.
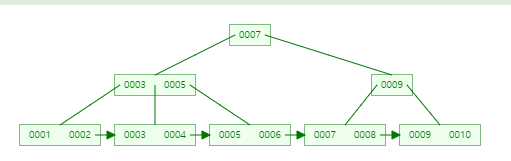
루트 노드와 내부 노드는 동일한 형태를 띄지만, 리프 노드 형태가 조금 다른 것을 확인할 수 있다.
B+TREE는 리프 노드에 루트 노드와 내부 노드가 포함되며, 연결 리스트로 연결되어 있다.
B-TREE는 탐색을 위해 노드를 찾아 이동해야하지만, B+TREE는 리프 노드에 모든 키값들이 정렬되어 있기 때문에 탐색에 있어 더 유리하다.
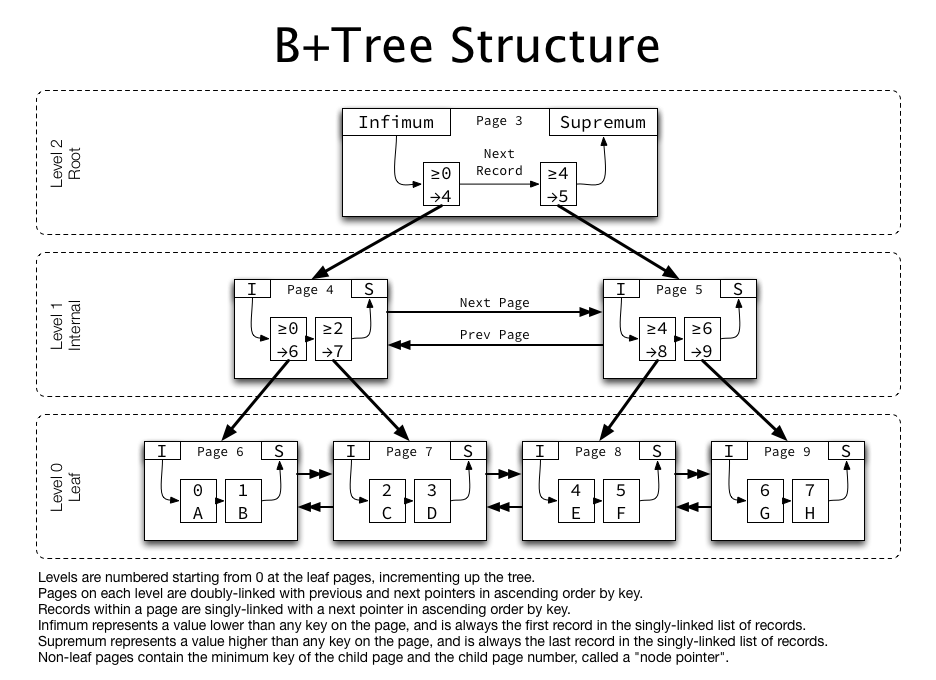
위 그림은 InnoDB에서 사용되는 B+TREE 구조이다.
InnoDB는 B+TREE 보다 더 복잡하다.
InnoDB에서는 같은 레벨의 노드들끼리는 Linked List가 아닌 Double Linked List로 연결되었으며, 자식 노드들은 Single Linked List로 연결되어 있다.
B+Tree 구조에서는 각 키의 범위에 따라 다음에 가야 할 페이지 넘버를 가리키는 포인터가 있다. 이 포인터를 통해 빠르게 다음 노드로 넘어갈 수 있다.
리프 노드에 도착하면, 여기서 디스크에 저장된 데이터의 주소를 확인할 수 있다. 또한, 리프 노드는 Linked List로 연결되어 있어, 이 리스트를 통해 데이터를 순차적으로 탐색할 수 있는 것이다.
데이터베이스 인덱스 [mysql]
데이터베이스에서 인덱스는 데이터를 조회할 때 모든 레코드에서 찾는게 아니라 검색 대상 레코드 범위를 줄일 수 있게 해준다.
CREATE TABLE employee (
emp_no INT NOT NULL AUTO_INCREMENT,
name VARCHAR(64) NOT NULL,
department VARCHAR(64),
hire_date DATE,
PRIMARY KEY (emp_no),
INDEX idx_name (name),
INDEX idx_department (department)
);예시로 employee라는 테이블을 만들어 보았다.
이 CREATE TABLE 문은 idx_name과 idx_department라는 두 개의 인덱스를 포함하고 있다.
이 테이블에 대해 인덱스를 활용한 SELECT 문의 예를 몇 가지 들어보면 다음과 같다.
- 이름으로 검색 (idx_name 인덱스 사용):
SELECT * FROM employee WHERE name = '홍길동';- 부서로 검색 (idx_department 인덱스 사용):
SELECT * FROM employee WHERE department = '개발팀';- 부서별 직원 수 조회 (idx_department 인덱스 사용):
SELECT department, COUNT(*) as employee_count
FROM employee
GROUP BY department;- 이름과 부서로 동시에 검색 (복합 조건에서 두 인덱스 모두 활용 가능):
SELECT * FROM employee
WHERE name LIKE '김%' AND department = '인사팀';이러한 쿼리들은 idx_name과 idx_department 인덱스를 활용하여 검색 속도를 향상시킬 수 있다. 대량의 데이터에서 특정 이름이나 부서를 검색할 때 효과적이다.
인덱스의 효과를 확인하려면 EXPLAIN 명령어를 쿼리 앞에 붙이면 확인할 수 있다.
EXPLAIN SELECT * FROM employee WHERE name = '홍길동';
실제로 사용된 인덱스가 idx_name 이고, extra를 보면 Using index condition라고 출력한다. 이는 인덱스를 효과적으로 활용하고 있다는 것을 의미한다.

테이블의 인덱스를 보면 Index_type이 BTREE인 것을 확인할 수 있다.
이런 인덱스 사용은 기본 원칙을 따르면, SQL 문을 더욱 효율적으로 작성할 수 있을 것이다.
인덱스 사용의 기본 원칙
1. INSERT, UPDATE, DELETE 작업이 많은 경우 인덱스 사용 자제
쓰기 작업이 빈번한 테이블에는 인덱스를 최소한으로 사용하는 것이 좋다.
인덱스는 데이터를 삽입하거나 수정, 삭제할 때마다 인덱스 구조를 업데이트해야 하기 때문에 쓰기 성능을 저하시킬 수 있다.
2. 조건절을 사용한 SELECT(읽기) 작업이 많은 경우 인덱스 사용
데이터 검색, 조회, 정렬, JOIN, 집계 등에서 성능을 높이기 위해 인덱스를 사용하는 것이 좋다.
특히 다음과 같은 상황에서 인덱스를 사용하면 효율적이다.
검색 쿼리가 자주 발생할 때: WHERE 조건에 자주 사용되는 열에 인덱스를 추가하면 검색 속도가 빨라진다.
정렬이 자주 필요할 때: ORDER BY가 자주 사용되는 열에 인덱스를 추가하면 성능이 향상된다.
JOIN을 자주 사용할 때: 테이블 간의 JOIN에 사용되는 열(기본 키 또는 외래 키)에 인덱스를 추가하면 JOIN 성능이 크게 개선된다.
집계 함수(GROUP BY, COUNT, SUM, MAX, MIN)를 사용할 때: 인덱스가 집계 작업의 속도를 높여준다.



👍👍👍👍👍