관계형 데이터베이스(Relational Database)의 핵심 개념인 관계 대수(Relational Algebra)와 그 전제 개념들을 정리합니다.
📌 관계(Relation)의 개념
✅ 구성 요소
- 스키마(Schema): 테이블 구조 정의.
예) 도서(도서번호, 도서이름, 출판사, 가격) - 인스턴스(Instance): 실제 데이터.
- 튜플(Tuple): 한 행(Row)
- 속성(Attribute): 열(Column)
- 도메인(Domain): 속성이 가질 수 있는 값의 집합.
✅ 특징
- 각 속성은 단일 값(atomic value).
- 속성 이름은 중복되지 않음.
- 튜플은 중복되지 않음, 순서와 무관.
- 속성도 순서와 무관.
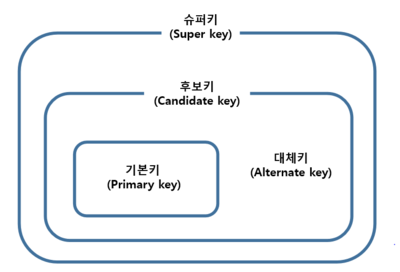
🔑 Key 개념
이미지 출처: https://wiki1.kr/index.php/%EC%88%98%ED%8D%BC%ED%82%A4
1. 슈퍼 키(Super Key)
- 튜플을 유일하게 식별할 수 있는 속성들의 집합.
- 유일성은 만족하지만 최소성은 만족하지 않을 수 있음.
2. 후보 키(Candidate Key)
- 슈퍼 키 중 최소성을 만족하는 키.
- 여러 개가 있을 수 있음.
- 두개 이상의 attribute로 이루어진 key를 composite key
- candidate key는 primary key와 alternate key로 구성
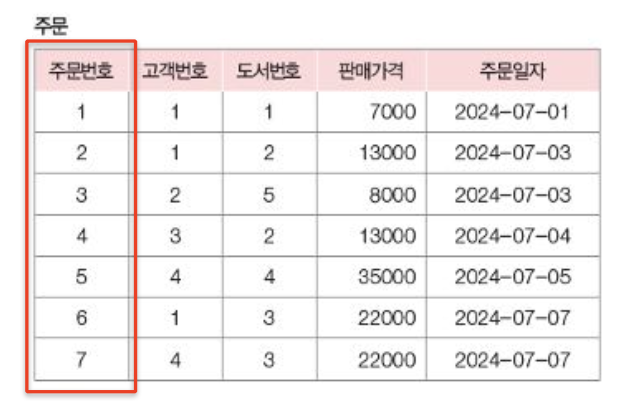
3. 기본 키(Primary Key)
- 후보 키 중 하나를 선정한 대표 키.
- relation내 tuple을 식별할 수 있는 고유한 값을 가져야 함
- NULL 불가, 유일해야 하며 변경 불가.
- 최대한 적은 수의 attribute를 가질 것
- primary key는 relation schema를 표현할때 밑줄을 그어 표시

4. 대체 키(Alternate Key)
- 기본 키로 선택되지 않은 나머지 후보 키.
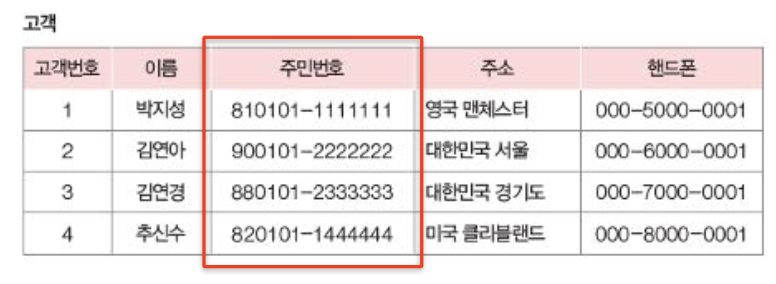
5. 대리 키(Surrogate Key)
- artificial key
- 의미 없는 인공 키. 예: 일련번호
- 복합 키가 너무 복잡하거나 적절한 키가 없을 때 사용.
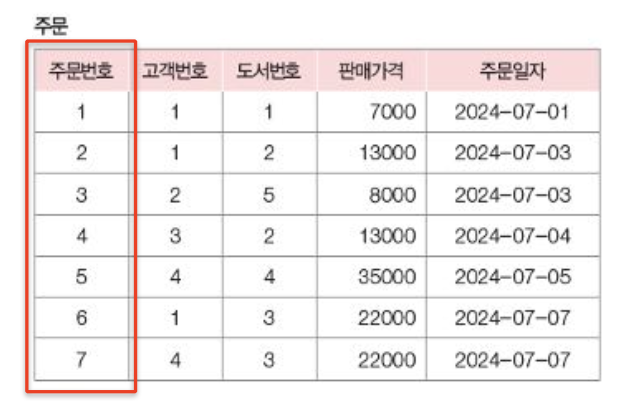
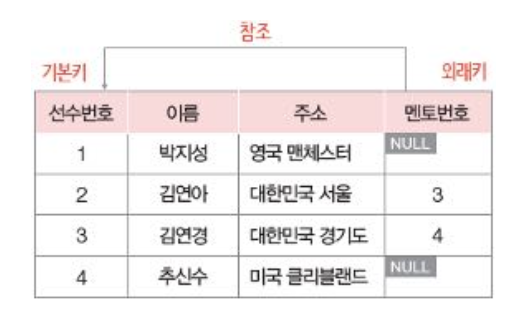
6. 외래 키(Foreign Key)
- 다른 테이블의 기본 키를 참조.
- 테이블 간 관계를 형성 (참조 무결성 유지).
- 참조하는 relation과 참조되는 relation이 같을 수 있음 (자신의 PK를 참조)
🧱 무결성 제약조건 (Integrity Constraints)
데이터베이스에서 "무결성 제약조건"이란 데이터의 일관성과 정확성을 보장하기 위한 규칙임.
이 제약조건은 데이터 삽입/수정/삭제 시 잘못된 값이 들어오는 것을 막아주는 장치이기도 함.
1. 도메인 무결성 제약조건 (Domain Integrity Constraint)
| 항목 | 설명 |
|---|---|
| 제약 대상 | 속성 (컬럼 하나하나) |
| 다른 이름 | 도메인 제약 (domain constraint) |
| NULL 허용 여부 | ✅ 허용 |
| 제약조건의 개수 | 속성의 수와 동일 |
| 기타 | 튜플 삽입/수정 시 해당 속성 값이 도메인 범위 내에 있어야 함 |
🧠 예시:
나이 속성은 반드시 20~100 사이의 숫자만 들어올 수 있게 설정할 수 있음.
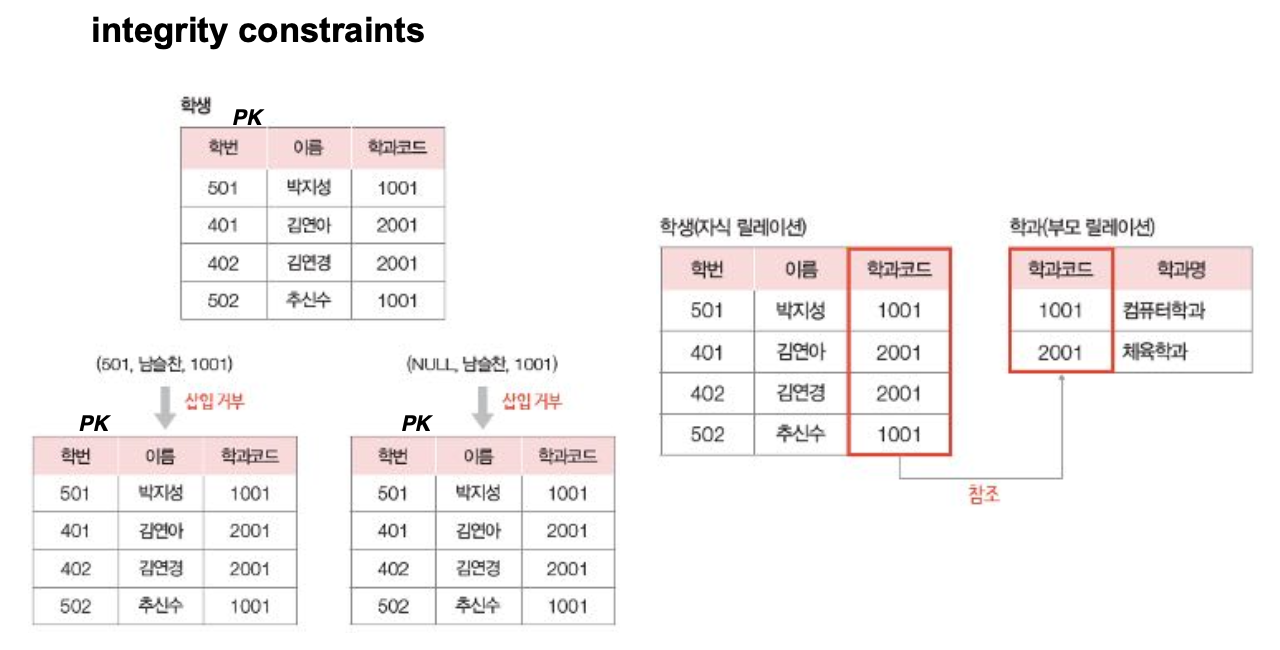
2. 개체 무결성 제약조건 (Entity Integrity Constraint)
| 항목 | 설명 |
|---|---|
| 제약 대상 | 튜플 (테이블의 행) |
| 다른 이름 | 기본키 제약 (primary key constraint) |
| 해당 키 | 기본키(Primary Key) |
| NULL 허용 여부 | ❌ 불가 |
| 제약조건의 개수 | 1개 |
| 기타 | 기본키는 반드시 고유하고 존재해야 함. 삽입 시 중복되거나 NULL이면 삽입 거부됨 |
🧠 예시:
학번이 기본키인 학생 테이블에서 학번=501이 이미 존재하거나, 학번=NULL이면 삽입 불가.
3. 참조 무결성 제약조건 (Referential Integrity Constraint)
| 항목 | 설명 |
|---|---|
| 제약 대상 | 속성과 튜플 |
| 다른 이름 | 외래키 제약 (foreign key constraint) |
| 해당 키 | 외래키(Foreign Key) |
| NULL 허용 여부 | ✅ 허용 (설정 가능) |
| 제약조건의 개수 | 0~여러 개 |
| 기타 | - 자식 테이블에서 외래키가 부모 테이블의 값과 일치해야 함 - 부모에 없는 값을 참조하려 하면 오류 발생 |
🧠 예시:
학생 테이블의 학과코드는 학과 테이블의 학과코드를 참조함.
→ 존재하지 않는 학과코드(3001 등)는 삽입 ❌
🔄 참조 무결성 삭제 정책 (부모 튜플 삭제 시 대처 방식)
부모 테이블에서 튜플 삭제 시, 자식 테이블이 참조하고 있으면 문제가 발생할 수 있습니다.
이를 방지하기 위해 삭제 옵션을 설정할 수 있습니다:
| 명령어 | 의미 | 예시 |
|---|---|---|
| RESTRICTED | 부모 릴레이션 삭제 거부 | 학과 테이블의 학과코드=1001 삭제 시 학생 테이블이 참조 중이면 삭제 ❌ |
| CASCADE | 자식 튜플도 같이 삭제 | 학과 삭제 시 학생도 같이 삭제 |
| DEFAULT | 자식의 외래키를 기본값으로 변경 | 학과코드가 미리 지정된 값으로 자동 설정 |
| NULL | 자식의 외래키를 NULL로 변경 | 학과 삭제 시 해당 학생의 학과코드가 NULL (허용 설정 필요) |
✅ 무결성 제약조건 핵심 요약 비교표
| 구분 | 도메인 제약 | 개체 무결성 | 참조 무결성 |
|---|---|---|---|
| 제약 대상 | 속성 | 튜플 | 속성과 튜플 |
| 다른 용어 | domain constraint | primary key constraint | foreign key constraint |
| 키 적용 | – | 기본키 | 외래키 |
| NULL 허용 여부 | 허용 | ❌ 불가 | 설정 가능 |
| 개수 | 속성 수와 동일 | 1개 | 0 ~ 여러 개 |
| 삽입/수정 시 유의사항 | 도메인 범위 확인 | 중복/NULL ❌ | 참조 무결성 유지 확인 |
📘 관계 대수(Relational Algebra)
관계 대수는 절차적 질의 언어로서, 관계(테이블)를 입력으로 받아 또 다른 관계를 출력으로 생성하는 연산 집합.
🔸 관계 대수의 특징
- 절차적 언어: 어떤 데이터를 어떻게 연산할지 순서를 명확히 지시
- 입력과 출력 모두 릴레이션(테이블)
🔹 집합 연산의 개념
관계 대수는 집합 이론에 기반한 연산으로 구성됩니다.
예를 들어, 다음과 같은 두 집합이 있다고 할 때:
A = {2, 4}
B = {1, 3, 5}
Cartesian Product (카티션 곱)
• 두 집합 A, B의 가능한 모든 조합
• 릴레이션 간 곱 연산이며, 조인(join)의 기초가 됨.
• A × B 결과: {(2,1), (2,3), (2,5), (4,1), (4,3), (4,5)} → 총 6개
📌 단항 연산자 (Unary Operator)
| 연산자 기호 | 이름 (한글) | 설명 | 예시 |
|---|---|---|---|
| σ (시그마) | 선택 (Selection) | 조건을 만족하는 튜플(행) 만 선택 | σ가격 ≤ 8000(도서) |
| π (파이) | 투영 (Projection) | 특정 속성(열) 만 추출. 중복 제거 | π이름, 주소(고객) |
📌 이항 연산자 (Binary Operators)
이항 연산자는 두 개의 릴레이션에 대해 연산을 수행하는 관계 대수 연산자임.
크게 집합 기반 연산자와 조인 연산자로 나눌 수 있음.
🔹 1. 집합 연산자 (Set Operators)
| 연산자 기호 | 이름 (한글) | 설명 | 예시 |
|---|---|---|---|
| ∪ | 합집합 (Union) | 두 릴레이션의 튜플을 합침 (중복 제거) | 도서A ∪ 도서B |
| ∩ | 교집합 (Intersection) | 두 릴레이션에 공통으로 존재하는 튜플만 선택 | 도서A ∩ 도서B |
| − | 차집합 (Difference) | 첫 릴레이션에만 존재하고 두 번째에는 없는 튜플 선택 | 도서A − 도서B |
| × | 카티션 곱 (Cartesian Product) | 두 릴레이션의 모든 가능한 튜플 조합 생성 | 고객 × 주문 |
🔹 2. 조인 연산자 (Join Operators)
조인은 두 릴레이션을 공통된 속성이나 조건을 기준으로 결합하는 연산.
조인 연산자는 가장 많이 쓰이며, 여러 가지 유형이 존재함.
| 조인 종류 | 설명 | 조건/기준 | 특징 | 예시 |
|---|---|---|---|---|
| Theta Join | 두 릴레이션의 튜플을 일반 조건에 따라 조인 | 비교 연산자 사용 (=, >, <, 등) | 가장 범용적, 다양한 조건으로 조인 가능 | 고객 ⨝고객.나이 > 주문.수량 주문 |
| Equi Join | Theta Join 중에서 속성 값이 같은 경우만 조인 | = 연산자만 사용 | 중복 속성이 그대로 남음 | 고객 ⨝고객번호 = 고객번호 주문 |
| Natural Join | Equi Join에서 중복 속성을 제거한 형태 | 공통 속성 자동 매칭 (= 조건 암묵적) | 중복된 속성 1개만 남기고 자동 결합, 가장 직관적이고 많이 사용 | 고객 ⨝ 주문 |
| Left Outer Join | 왼쪽 릴레이션 기준 조인, 실패한 튜플도 포함 | 왼쪽 기준, 실패 시 NULL | 왼쪽 데이터는 모두 유지됨 | 고객 ⟕ 주문 |
| Right Outer Join | 오른쪽 릴레이션 기준 조인, 실패한 튜플도 포함 | 오른쪽 기준, 실패 시 NULL | 오른쪽 데이터는 모두 유지됨 | 고객 ⟖ 주문 |
| Full Outer Join | 양쪽 릴레이션 기준, 실패한 튜플도 모두 포함 | 둘 다 실패 시 NULL | 왼쪽/오른쪽 모두 유지, 누락 없는 전체 결합 | 고객 ⟗ 주문 |
🧠 예제 연산 표현
-
도서 테이블에서 가격이 8000원 이하인 도서이름과 출판사 조회:
π도서이름, 출판사(σ가격≤8000(도서)) -
고객과 주문 테이블을 고객번호로 조인하고 이름이 '박지성'인 튜플에서 주문번호, 이름, 판매가격 출력:
π주문번호, 이름, 판매가격(σ이름='박지성'(고객 ⨝ 주문))
✅ 마무리
관계 대수는 단순한 데이터 필터링을 넘어서 관계형 데이터의 연산 논리를 표현하는 강력한 도구임.
📚 공부 팁
- Selection/Projection 등 기본 연산은 SQL과 매칭해보며 연습
- 조인 연산은 Natural Join vs Outer Join 차이를 명확히!
- 키 개념(Primary, Foreign, Candidate 등)은 ERD 설계에서 필수

