why) 소개하는가? DNN에 앞서 shallow NN을 먼저 설명

1. What is NN?

인간의 뇌의 구조와 기능에서 영감을 받은 Machine learning 모델의 유형
Neuron(Regressor) 으로 이루어짐.

❓ For) Data 내부의 패턴을 학습 || 그러한 패턴에 기반한 예측
❕ How) Learn in each Neuron
→ log. R과 forward prop., back prop.을 이용해 Cost function을 최소화하는 방향으로 w, b를 업데이트함.
1. forward propagation (추정값 $\hat y$ 도출)
2. loss 함수 정의: $L(\hat y, y)$ where y=ground truth
3. back propagation (뒤로 가며 미분)
➰ Ex) Feedforward NN, CNN, RNN, etc

• noation:
  • [i]: i-th layer
  • (i): i-th example

2. 2 Layer NN (Shallow NN)

Neural Net. Representation

• [0] Input layer
• [1] hidden layer
• [2] output layer

why) Transpose 사용?
→ Matrix Multiplication의 편의성

❕ how) Computing NN’s Output

• notation
  • Transpose 기호 생략. 그러나 Transpose되어 있는 거임.

각 Neuron에서는 다음과 같은 연산이 이루어짐
Given input $x$ :

👍🏻 gd) Vectorizing across multiple examples (Mat. Mult.)

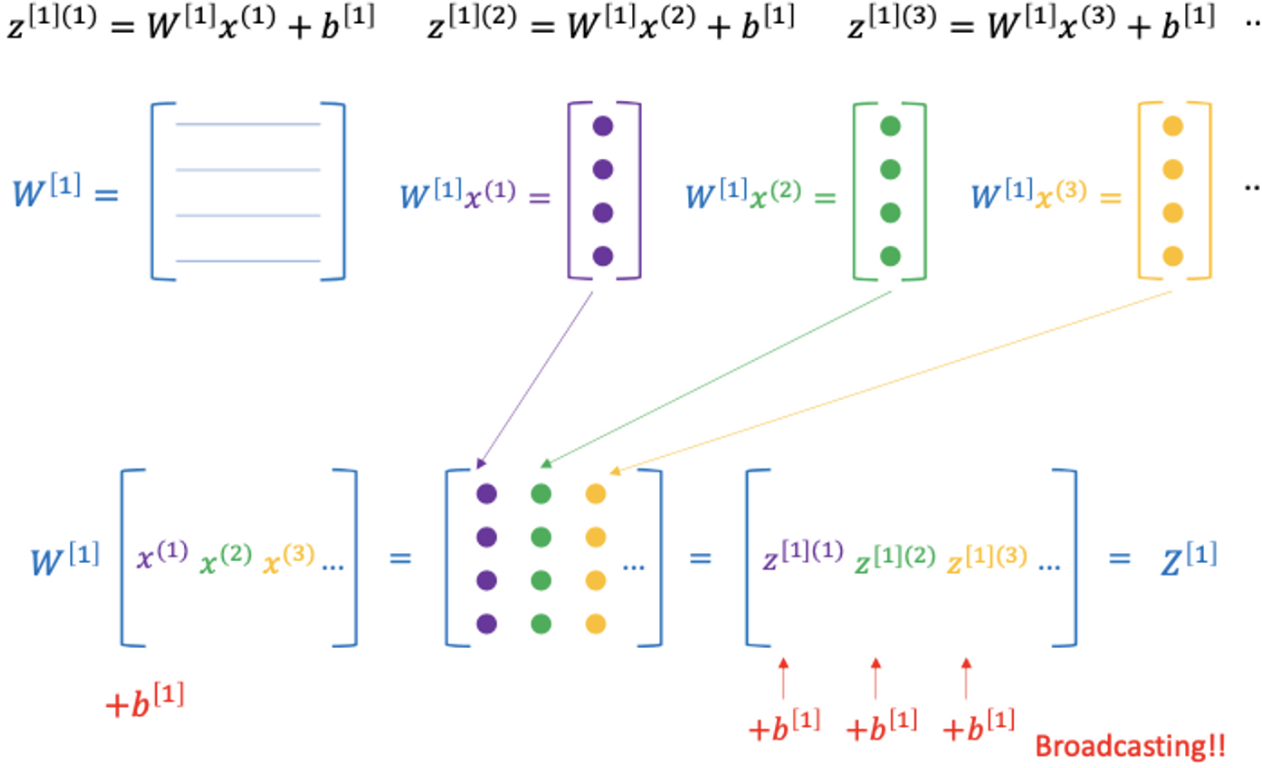🥲 Pb) m개의 data에 대하여 Log. R 따로 계산하면 (for-loop 사용하면) inefficient → Sol) x→ vector, W → matrix로 만들어주면, GPU로 병렬 연산이 가능해서 효율성 gd

➰ ex) 2NN, Deep-NN

1) 2 Layered NN by Gradient Descent
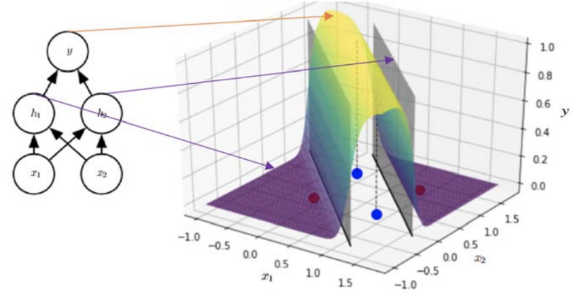
하나의 hyperplane는 linearly seperable한 함수에 대해서만 표현할 수 있다.
NN은 위와 같은 한 평면에 있는 (위와 같은) red, blue를 분류할 수 있는 모델을 만들 수 있다.

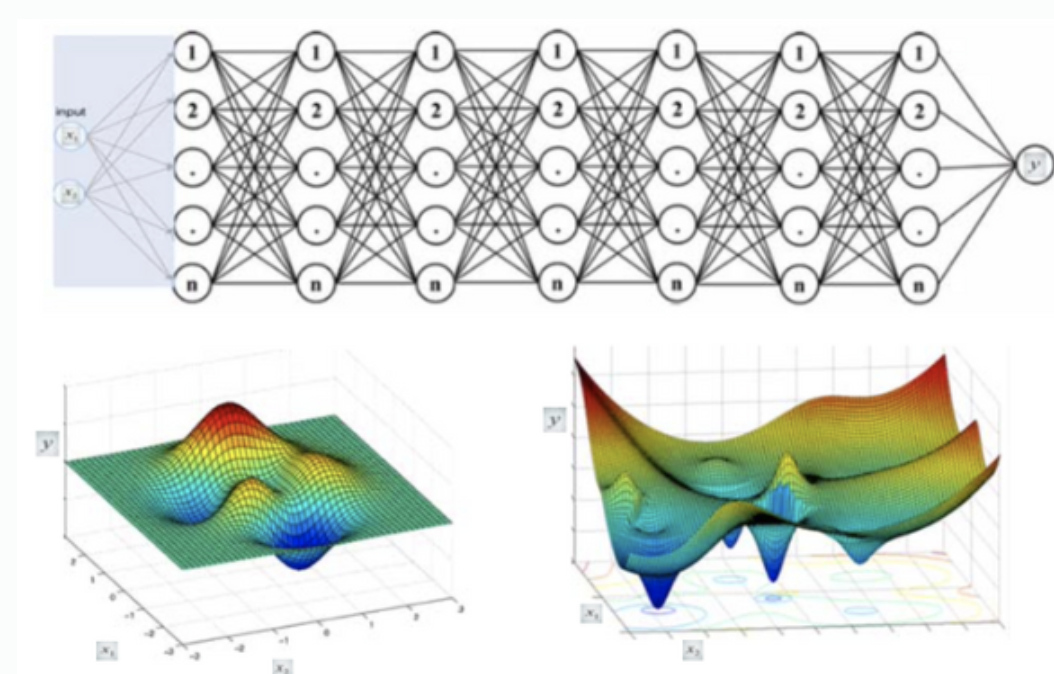
2) Another Ex.; Deep NN by GD
다음과 같은 복잡한 형태도 가능

3. Activation Function

• 여러 가지가 있으므로 모델링 시마다의 option

• Sigmoid -> 이진 분류

• tanh -> 다중 분류

  sigmoid function을 늘린 버전

  • 일반적으로! works better than sigmoid
  • 🥲 pb) vanishing gradient: z값이 커지거나, 작아지면 gradient는 거의0
    → sol) ReLU

• ReLu :

  gradient가 0 | 1

  • 👍🏻 계산량이 많지 않음에도 학습이 더 잘 되더라~

• Leaky ReLU

▶️ Binary Classification → output layer에서는 sigmoid가 일반적. ReLU는 무한히 커지므로 확률값을 표현하기가 어렵.

why) Act. Func. 으로 non-linear를 쓰는가?

• simple linear func.으로 학습하면 결국 linear combination이 되므로 경계 부분에서 급격하게 변하는 모델 → 실제 data와 다르다.
• linear가 적용되면, 그 layer가 없는 경우와 표현력이 크게 다르지 않음.

gd) Derivatives of act. func.

미분값이 적당하고 직관적임.

• sigmoid →
  • $dy = y(1-y)$
• tanh →
  • $dy = (1+y)(1-y)$
• ReLu →
  • $0 \ \ if\ z<0\\ 1\ \ if\ z>=0$
• Leaky ReLu →
  • $0.01 \ \ if\ z<0\\ 1\ \ if\ z>=0$