[JAVA] 순열과 조합

순열과 조합은 고등학교 2학년때인가 경우의 수를 배우면서 나오는 개념인데, 프로그래밍 문제에도 출제가 되니 개념부터 다시 떠올려보자

* 순열

순서가 있는 경우의 수

ex) a,b,c 3명의 학생을 한줄로 세울 수 있는 경우의 수를 구하여라.
-> 6가지 (abc, acb, bac, bca, cab, cba)

수학적 표기는 Permutation,
3개중 3개 순열 선택 : 3P3 이고 3P3 = 6 이다.

* 조합

순서가 없는 경우의 수

ex) a,b,c라는 구슬이 들어있는 주머니에서 2개를 꺼낼 수 있는 경우의 수를 구하여라.
-> 3가지 (ab, ac, bc)

수학적 표기는 Combination,
3개중 2개 조합 선택: 3C2 = 3 이다.

🍩 순열

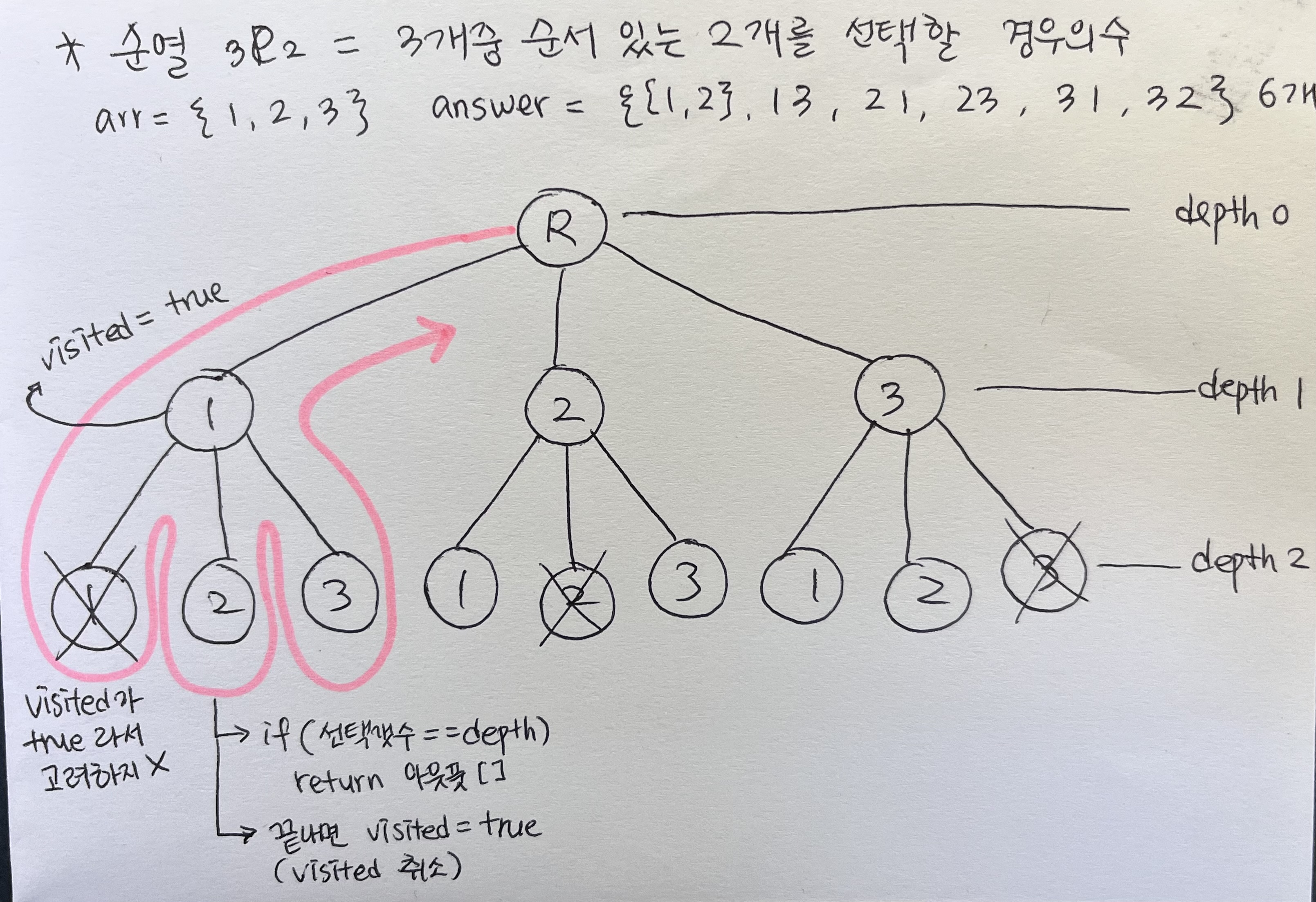
1. 알고리즘

2. 자바코드

Class Solution{
    boolean[] visited;
	public int main(int[] array, int select){
    	visited = new boolean[array.length];
        int[] result = new int[select];
        
    	combination(array, visited, result, select, 0);
        
    }
	
    public void combination(int[] array, int[] visited, int[] result, int select, int depth){
    	if(depth == select){
            System.out.println(Arrays.toString(result));
            return;
        }
        
    	for(int i = 0; i < array.length; i++){
        	if(!visited[i]){	// 처음 방문하는 숫자
                visited[i] = true;
            	result[depth] = array[i];
                combination(array, visited, result, select, depth+1);
                visited[i] = false;
            }
        }
    }

}

🍩 조합

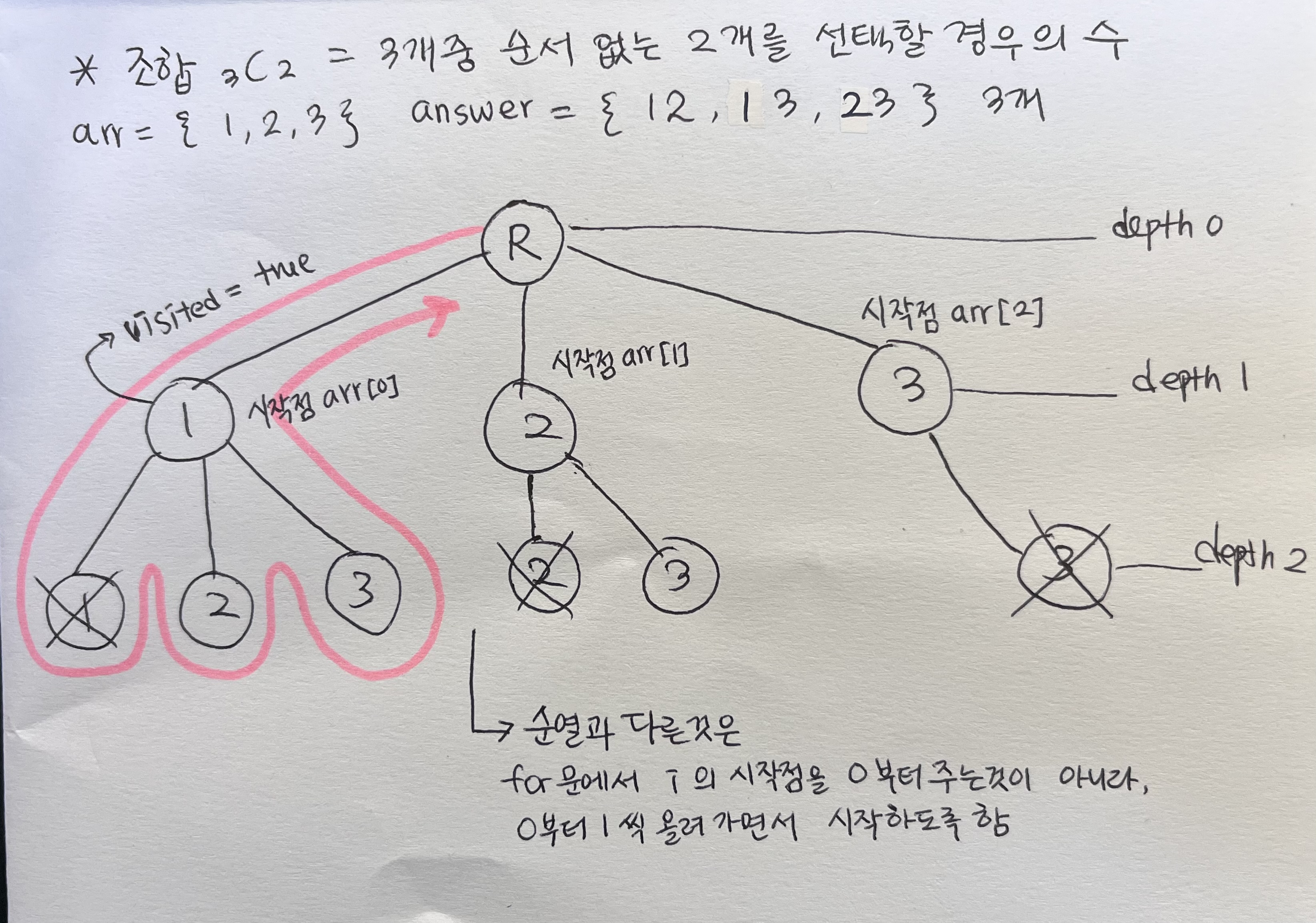
-> 시작점을 arr[0], ... 으로 적었는데, 중복은 어짜피 허용되지 않으므로 시작점을 a[1] 부터 순회하는 것이 더 효율적이겠다.

1. 알고리즘

2. 자바코드

Class Solution{
    boolean[] visited;
	public int main(int[] array, int select){
    	visited = new boolean[array.length];
        int[] result = new int[select];
        
    	combination(array, visited, result, select, 0);
        
    }
	
    public void combination(int[] array, int[] visited, int[] result, int select, int depth){
    	if(depth == select){
            System.out.println(Arrays.toString(result));
            return;
        }
        
    	for(int i = depth; i < array.length; i++){
        	if(!visited[i]){	// 처음 방문하는 숫자
                visited[i] = true;
            	result[depth] = array[i];
                combination(array, visited, result, select, depth+1);
                visited[i] = false;
            }
        }
    }

}