💡 비지도 학습 : 타겟이 없을때 데이터 패턴을 찾거나 구조를 파악하는 머신러닝
- 군집 : 비슷한 샘플끼리 그룹으로 모으는 작업
- 클러스터 : 군집 알고리즘에서 만든 그룹
☞ 문제 : 타깃이 없을때 과일 이미지를 종류별로 분류하는 방법?

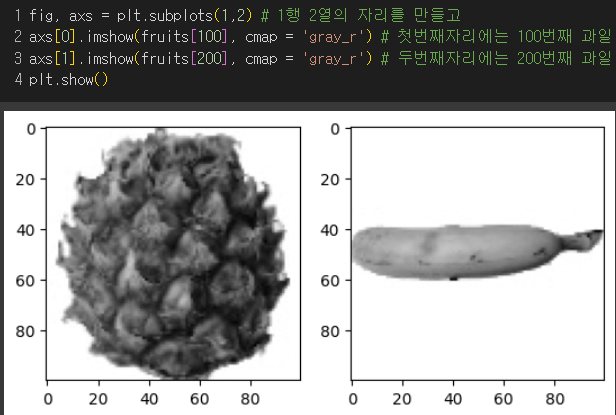
과일사진데이터의 처음 100개는 사과, 그 다음 100개는 파인애플, 나머지 100개는 바나나로 이루어져있다.
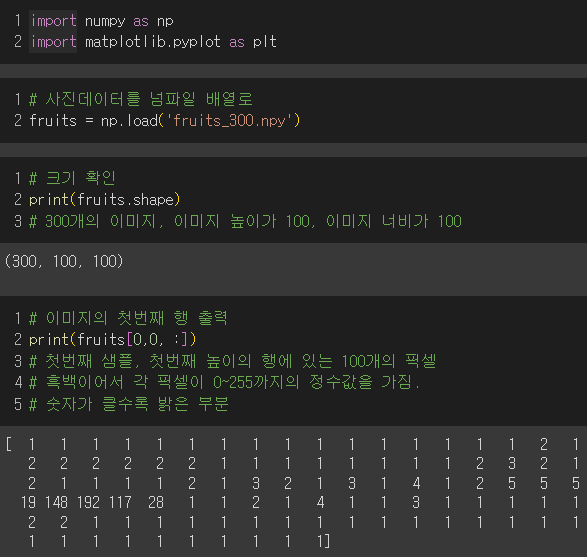
300개의 사진샘플이 있고, 하나의 샘플이 100 * 100의 픽셀로 이루어져있다고 생각하면 됨!
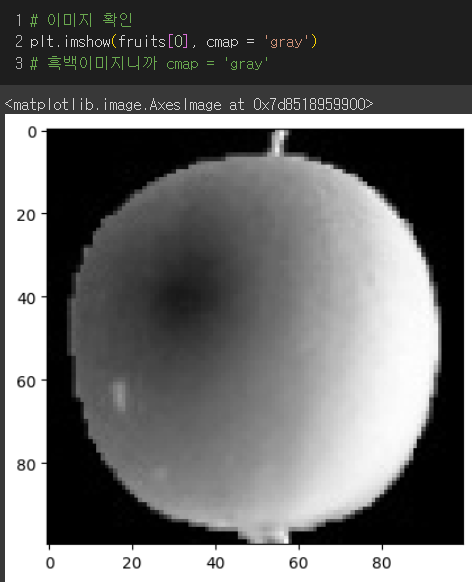
첫번째 이미지 : 어두운색(0) <----------------> 밝은색(255)

알아보기 좋게 흑백반전 이미지 : 밝은색(0) <----------> 어두운색(255)
큰 출력값에 의미부여하도록 만들어주는 것이 좋다!
2차원 배열을 1차원 배열로 만들어 주는 것이 계산할 때 좋다!

사과 샘플은 100개이고, 배열의 크기가 10000으로 변환되었다.

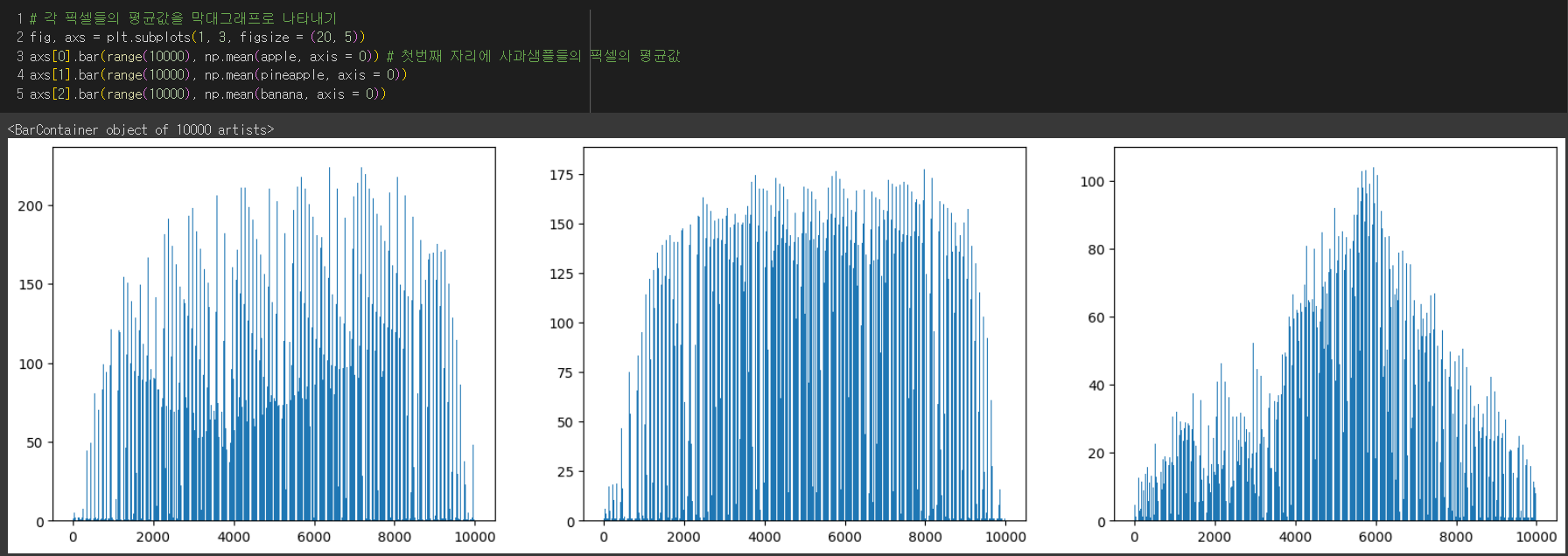
각 사과 샘플들 픽셀 평균을 계산한 결과
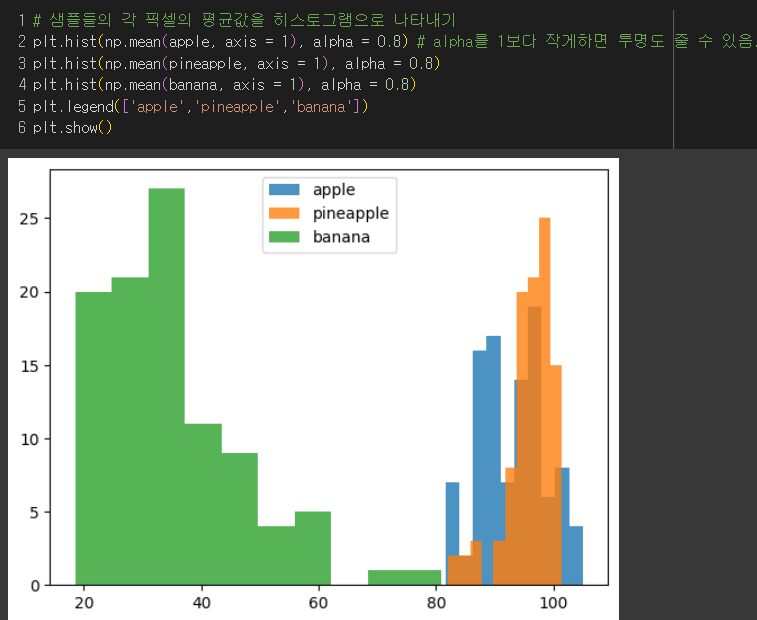
→ 바나나는 밝은 부분이 많고, 파인애플은 어두운 부분이 많다.
반면, 사과는 어두운 부분이 많은데 약간 덜 어두운 부분과 고루 있는 편으로 보여진다.
→ 각 클러스터별로 막대그래프로 나타내보았더니
사과는 가운데 부분이 어둡고, 파인애플은 울퉁불퉁한 표면때문인지 오르락내리락하는 부분이 있고, 바나나는 정가운데 부분만 어두워서 그런지 정규분포처럼 보인다.

→ 평균값으로 만든 이미지인데 얼추 과일들의 이미지와 비슷하게 나온다.
☞ 그럼, 평균값에 가까운 이미지들을 골라보자!

먼저, (원래 fruits 데이터 - 사과 샘플의 평균)에 절댓값을 취해주고
그 값들의 평균을 구한 후
가장 작은 값 순서대로 100개를 골라서 이미지로 출력


→ 사과 샘플의 평균과 가까운 사진들이 모두 사과사진!! 🍎
바나나도 시도해보았다.
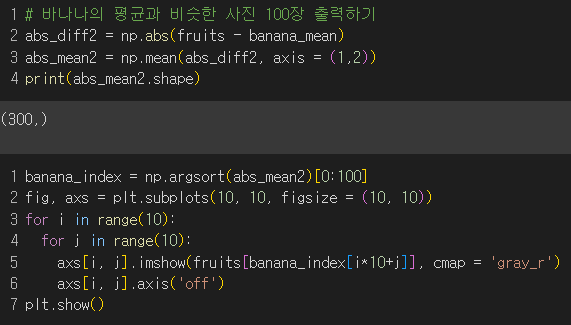

→ 바나나도 대부분 바나나 사진이 나왔다..! 🍌 눈치없는..사과...도..
☞ 진짜 비지도 학습일땐, 평균값을 구할 수 없다.
이럴땐!! k-means 알고리즘 사용!!!
- k-means 알고리즘 : 랜덤하게 정한 클러스터 중심(센트로이드)를 계속해서 업데이트하여 최적의 클러스터를 구성하는 알고리즘
① 임의로 k개의 클러스터 중심을 지정
② 각 샘플들을 가장 가까운 클러스터 중심으로 클러스터링 되도록 지정
③ 위와 같이 클러스터링된 샘플들의 평균값을 계산하여 새로운 클러스터 중심으로 변경
④ 클러스터 중심이 변하지 않을때까지 위의 과정을 반복
cf) 클러스터 중심(센트로이드) : k-means 알고리즘이 만든 클러스터에 속한 샘플들의 특성 평균값
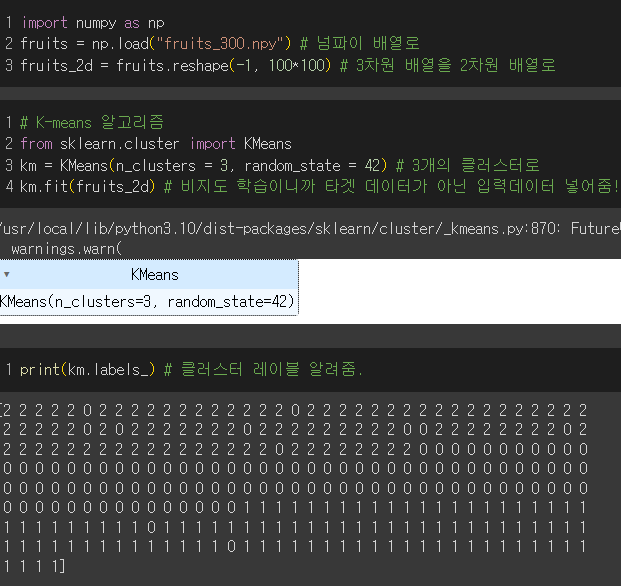
각 클러스터별 샘플의 개수를 확인한 후
각 클러스터를 확인하기 위해서 이미지를 출력해봐야 한다.
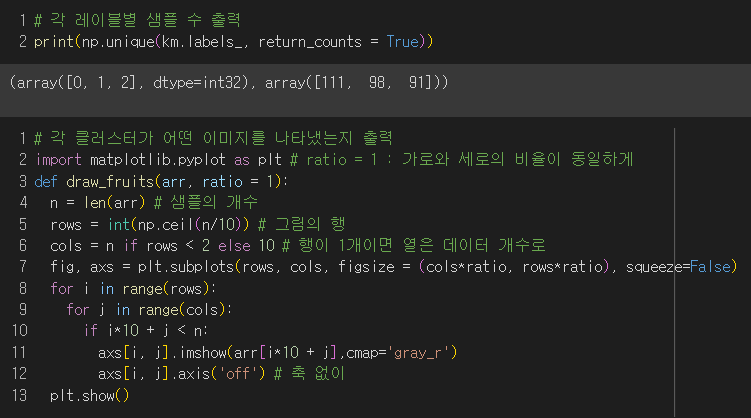






→ 첫번째 : 파인애플, 두번째 : 바나나, 세번째 : 사과
완벽하게 구분해내지는 못했지만 비지도 학습이니까 괜찮은 편!
🤔 근데 축을 없애려고 axis('off') 썼는데 책처럼 왜 깔끔하게 나오는게 아니라 축이 출력된건지....흠..
- 각 클러스터의 중심을 이미지로 출력해보자.
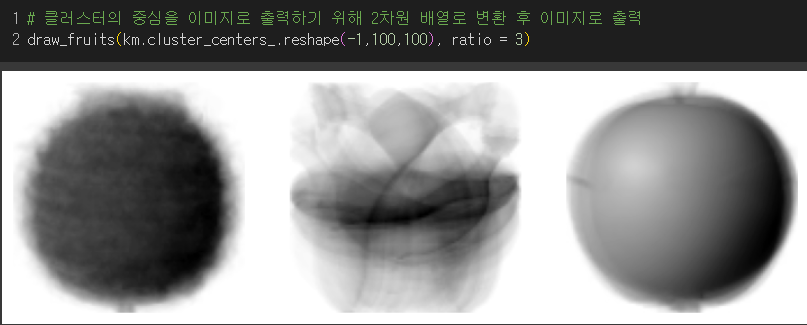
→ 클러스터와 비슷하게 출력됨.
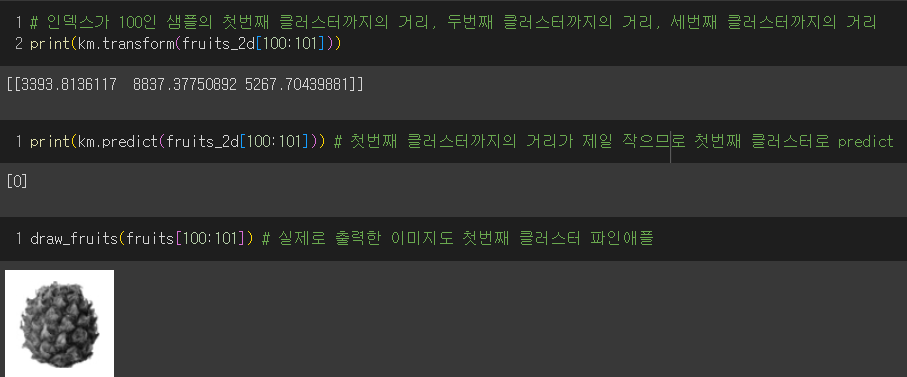
🚨 여기서 fruits_2d[100] 이라고 쓰면 (10000, )크기의 배열이 되므로 슬라이싱 연산자를 사용해서 fruits_2d[100:101]로 (1,10000) 크기의 배열을 전달해야 한다!!
→ 그렇게 나온 클러스터 중심까지의 거리는 첫번째 클러스터가 가장 가까웠고, 그래서 예측한 클러스터의 인덱스가 0이었다.
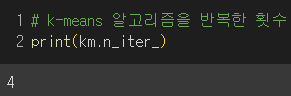
- 알고리즘을 반복한 횟수는 niter 속성에 저장된다.
✔️ 엘보우 방법 : 최적의 클러스터 개수 k 찾는 방법으로 클러스터의 개수를 늘려가면서 이너셔의 변화를 관찰
- 이너셔 : 클러스터 중심과 클러스터에 속한 샘플 사이의 거리의 제곱합
→ 클러스터에 속한 샘플이 얼마나 가깝게 모여 있는지를 나타내는 값
→ 클러스터의 수 ↑ → 각 클러스터 내 샘플수 ↓ → 이너셔 ↓
클러스터의 수를 증가시키면서 이너셔를 그래프로 그렸을때 꺾이는 지점부터는 클러스터의 수를 늘려도 클러스터에 밀집된 정도가 개선되지 않고, 이너셔가 더이상 줄어들지 않음.
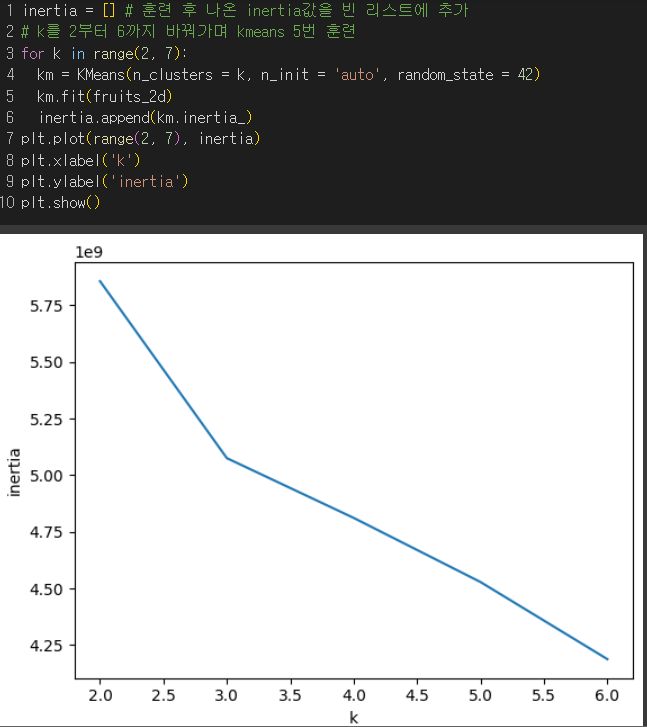
→ k =3 일때 이후로 기울기가 완만해졌음. 하지만 명확하게 줄어들지는 않았음.
☞ 너무 많은 사진 데이터를 줄일 수 있는 방법은? : 차원축소
데이터를 가장 잘 나타내는 일부 특성을 선택하여 데이터 크기를 줄이고 지도학습 모델의 성능을 향상시킬 수 있는 방법
ex) PCA(주성분분석)
-
차원
1차원배열(벡터)에서의 차원 : 원소의 개수
2차원이상의 배열에서의 차원 : 축
ex) 행, 열 -
주성분분석이란,
데이터에 있는 분산이 큰 방향을 찾는 것으로, 분산이 큰 방향은 더 잘 퍼져있어서 데이터를 고루 설명할 수 있다.
⭐ 주성분벡터 : 원본데이터에 있는 어떤 방향으로 주성분벡터의 원소갯수는 원본데이터에 있는 특성갯수와 같음.
⭐ 주성분은 원본 데이터와 차원이 같고 주성분으로 바꾼 데이터는 차원이 줄어듦!!!
⭐ 주성분이 가장 분산이 큰 방향이므로 주성분에 투영하여 바꾼 데이터는 원본이 가지고 있는 특성을 가장 잘 나타냄.
첫번째 주성분 벡터는 분산이 제일 큰 방향으로 찾아낸 후 그 다음 주성분 벡터는 첫 번째 벡터에 수직이고 분산이 가장 큰 방향을 찾음.
과일 이미지 데이터를 2차원 넘파이 배열로 바꾼 후 50개의 주성분으로 PCA 수행

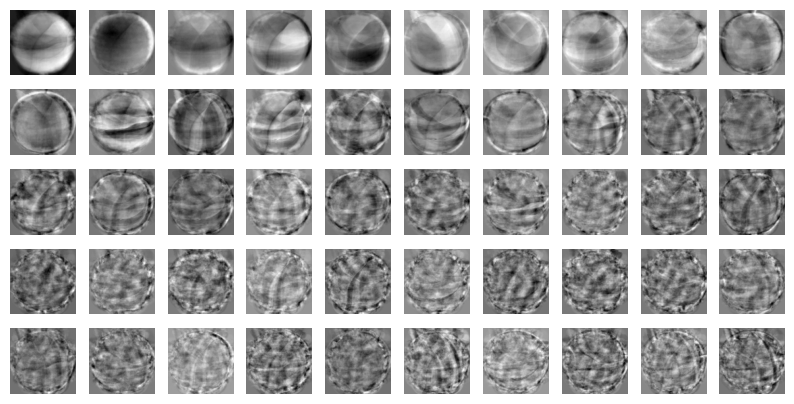
→ 첫번째 주성분이 가장 데이터를 잘 설명하므로 뚜렷하게 보이고 갈수록 흐릿해지고 알아볼 수 없는 경향이 보인다.

→ pca한 데이터는 원래 데이터보다 크기가 줄어들었다!
- pca한 데이터를 원래 데이터로 되돌리기
줄어든 차원에서 다시 원본 차원으로 손실을 최대한 줄이면서 복원할 수 있다.
 |  |  |
|---|
→ 50개의 특성이 분산을 가장 잘 보존하도록 변환되어 잘 복원됨!
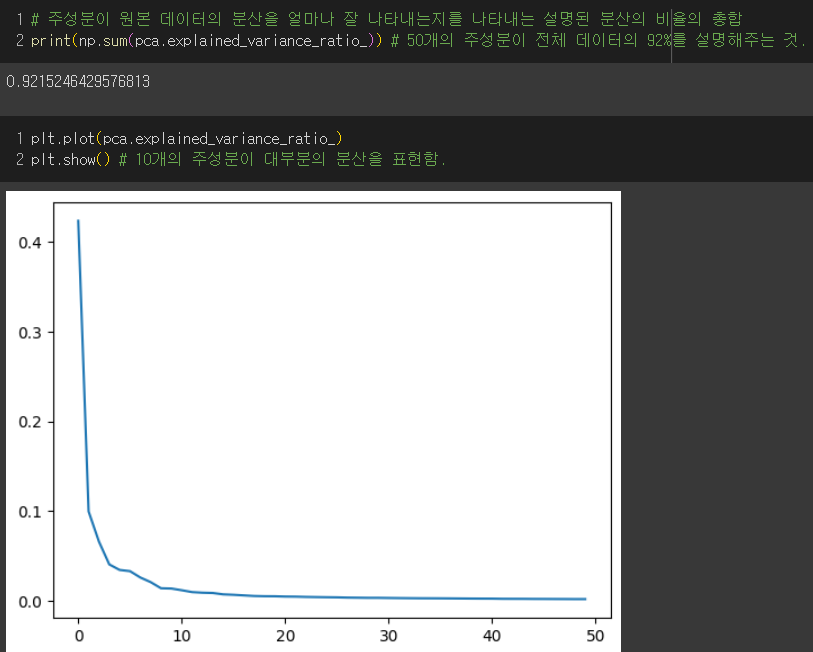
- 설명된 분산 : 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
🔥 원래 데이터 vs pca로 축소한 데이터
먼저, 로지스틱회귀로 교차 검증을 수행해보자.
교차검증시 타겟데이터가 필요하므로 생성 후 교차검증
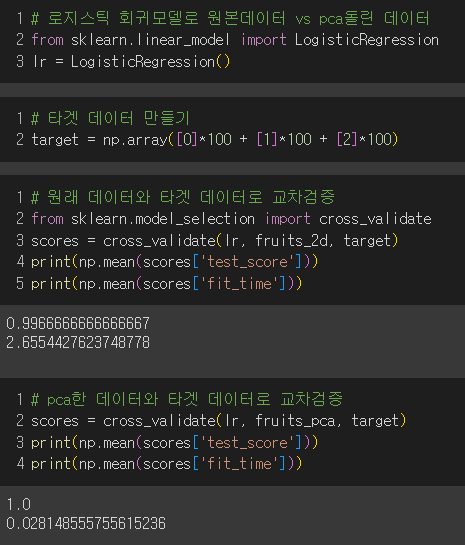
→ 50개의 특성을 사용해도 정확도가 100%가 나옴.
- 원하는 설명된 분산의 비율에 도달할 때까지 자동으로 주성분을 찾아보자!
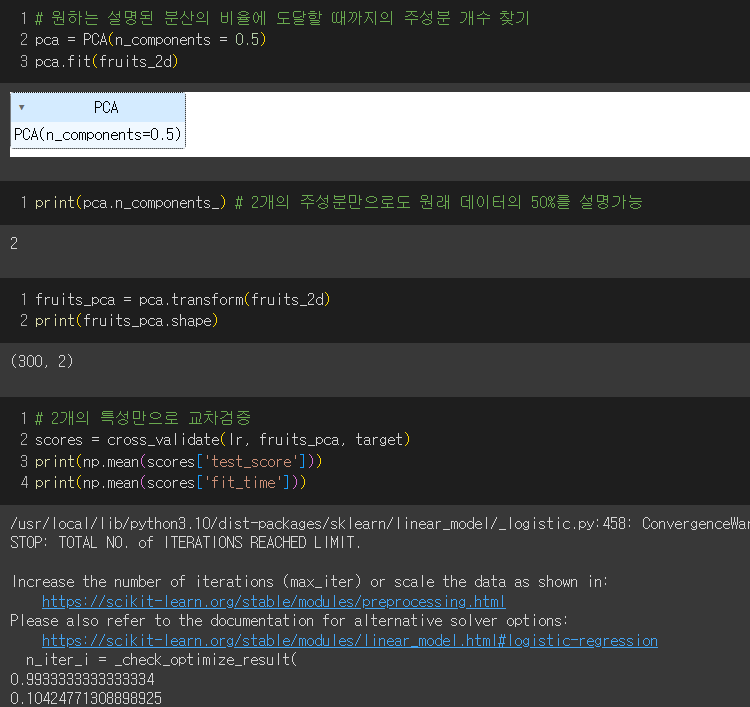
→ 2개의 특성만으로도 99%를 설명할 수 있다.
- 차원 축소된 데이터로 k-means 알고리즘으로 클러스터 찾기

 |  |  |
|---|
클러스터별로 나누어 산점도 그리기
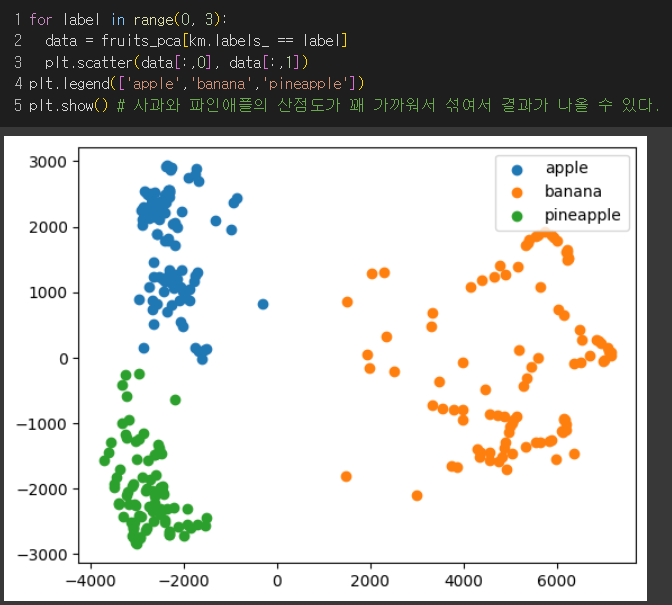
→ 2개의 특성만으로도 산점도가 잘 구분되는 양상이지만 사과와 파인애플은 겹치는 부분이 있어서 혼동을 일으킬 수 있을것.
선택미션
p.337 확인문제
1. ②
주성분 벡터의 원소 개수 = 원본 데이터셋에 있는 특정계수
-
①
샘플 수는 같으니까 1000그대로이고, 크기만 100개에서 10개로 줄어들었으므로 (1000,10) -
①
주성분의 분산이 가장 큰 것이므로 첫번째 주성분이다.