그리디 알고리즘이란?
- Greedy는 '탐욕스러운, 욕심 많은'이라는 뜻이다.
- 그리디 알고리즘은
선택의 순간마다최적의 해를 선택하여최종적인 해답에 도달하는 알고리즘이다. - 그리디 알고리즘으로 문제의 최종적인 해답에 도달하기 위해서는 탐욕적 선택 속성(Greedy choice property)과 최적 부분 구조(optimal substructure) 두 조건이 성립되어야 한다.
- 키워드 : 선택의 순간, 최적의 해, 최종적인 해답
선택의 순간, 최적해
예제 1. 다음과 같은 트리가 주어졌을 때, 루트 노드부터 시작해 거쳐가는 각 노드 값의 합을 최대로 만드는 프로그램을 만들어라!
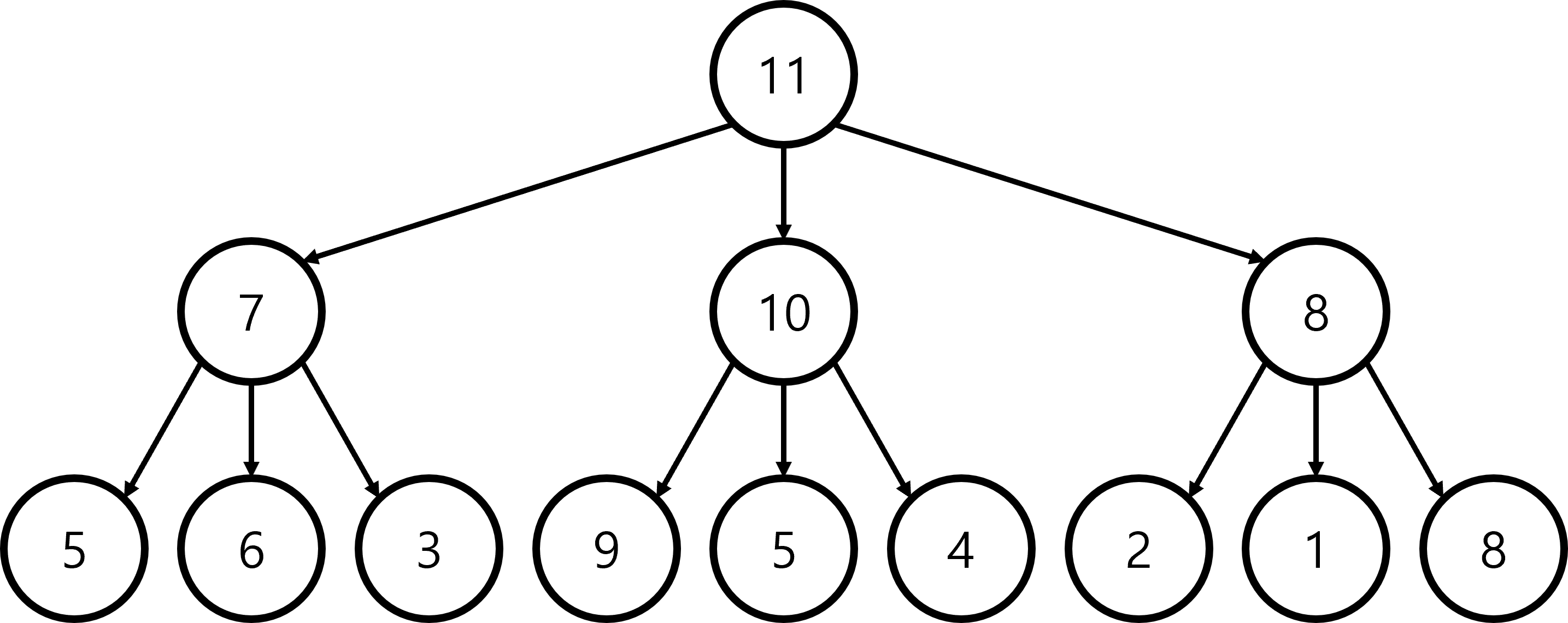
Q. 문제를 어떻게 풀 수 있을까?
A. 다음과 같은 방법으로 풀 수 있다.
- 탐색 방법 : 루트 노드에서 가능한 모든 경로를 더해본 후, 값이 가장 큰 노드를 선택한다.
- 그리디 방법 : 부모 노드에서 가장 큰 값을 갖는 자식 노드를 선택한다.
- 기타 등등
그리디 방법
- 선택의 순간 :
어떤 노드를 더할지 고려하는 순간이다.
- 최적의 해 :
가장 큰 값을 갖는 노드를 찾는 것이다.
그리디 알고리즘의 특징 :
- 모든 경우를 탐색하는 것보다 시간복잡도에서 우위에 있다.
- 최적 해를 떠올릴 수 있다면 직관적인 풀이가 가능하다.
- 하지만 모든 문제에 적용할 수 없다.
최종적인 해답
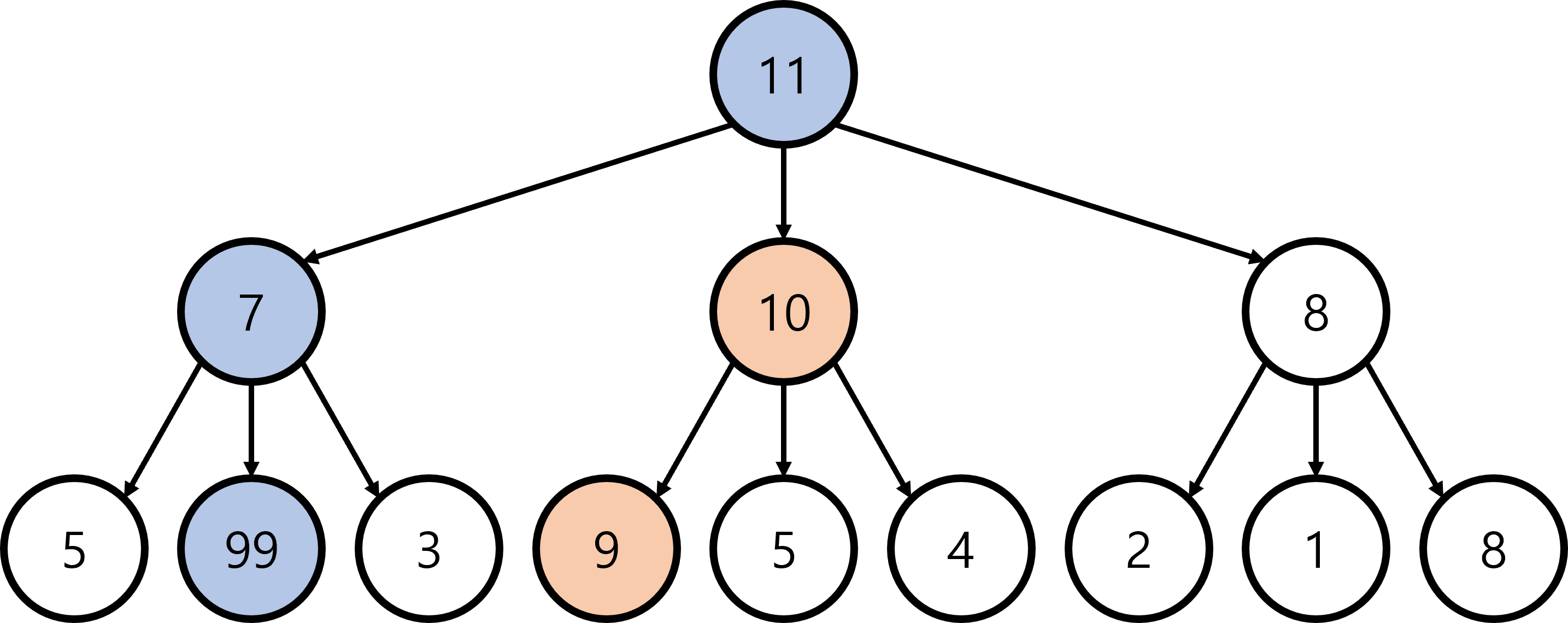
예제 2. 다음과 같은 트리가 주어졌을 때, 루트 노드부터 시작해 거쳐가는 각 노드 값의 합을 최대로 만드는 프로그램을 만들어라! (새로운 테스트 케이스)
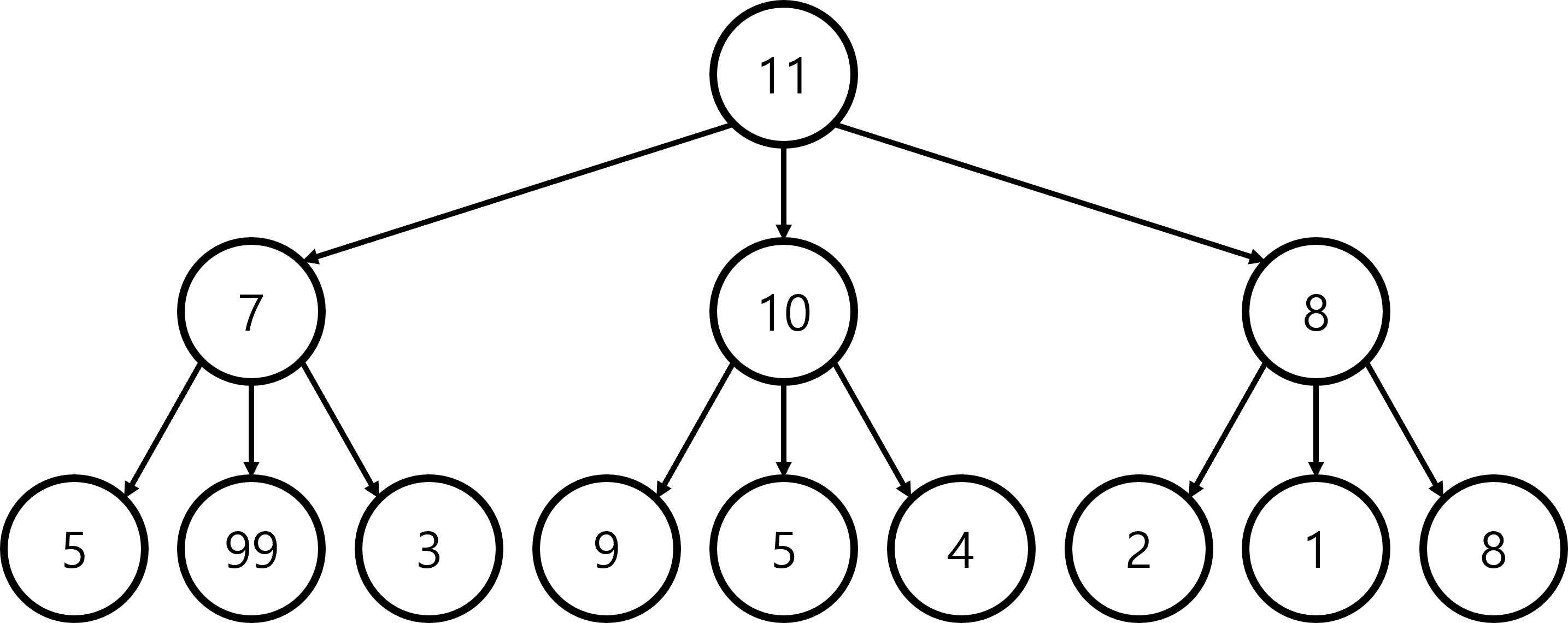
Q. 문제의 정답은 무엇일까? 즉, 최종적인 해답은 무엇일까?
A. 11 -> 7 -> 99 이 총합 117로 가장 큰 값을 갖는 경로이다.
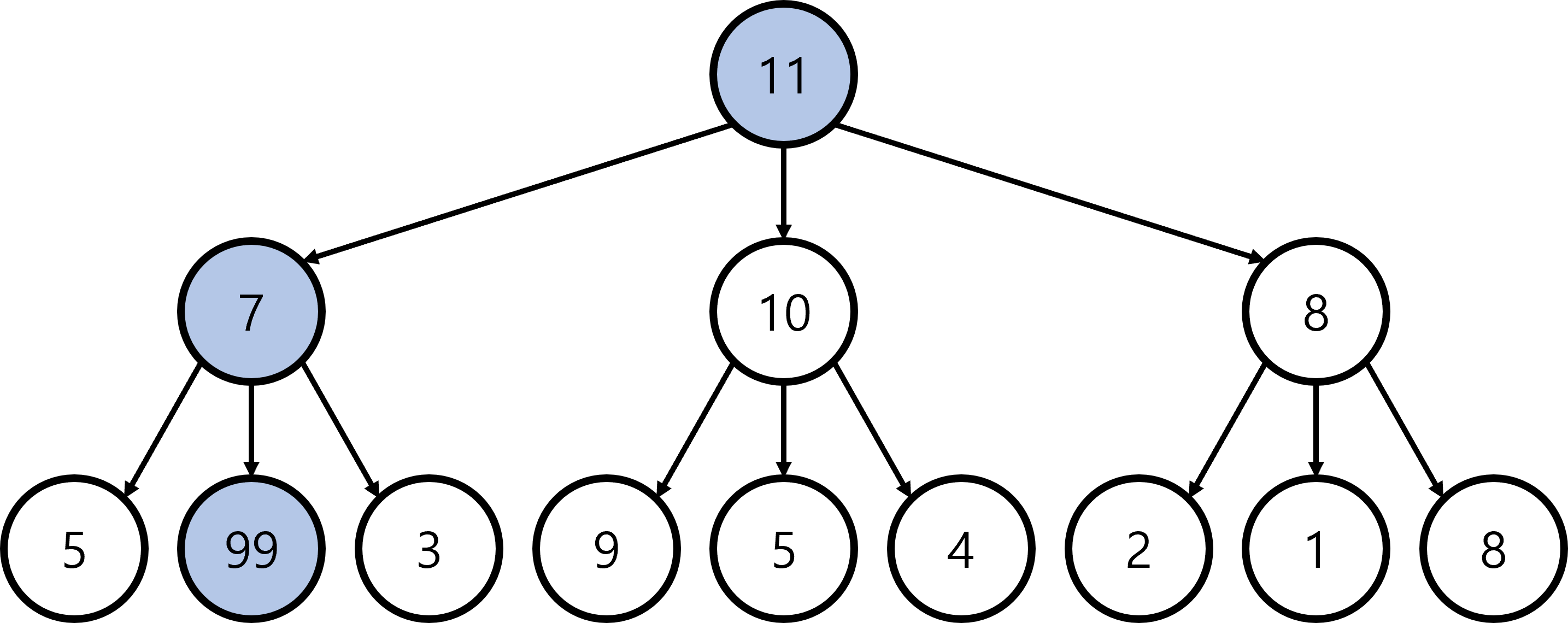
Q. 예제1에서 적용한 것과 같은 그리디 알고리즘을 사용하면 어떻게 될까?
A.
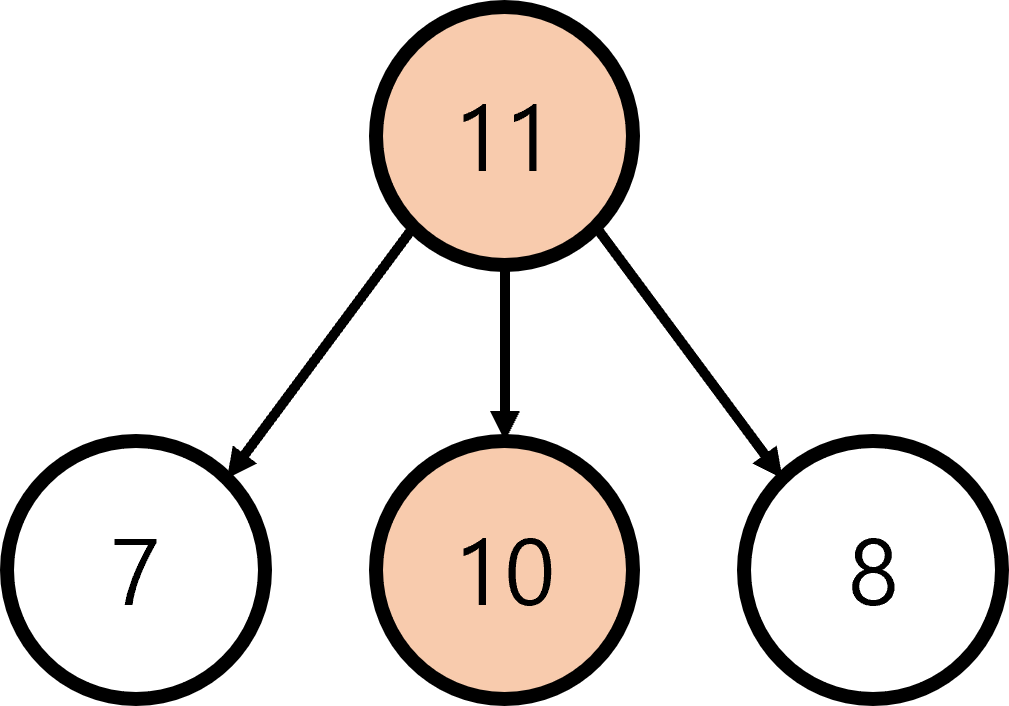
- 매 선택의 순간마다 가장 큰 값을 갖는 자식 노드를 선택해보자.
- 첫 번째로 가장 큰 값을 갖는 10 노드를 선택한다.
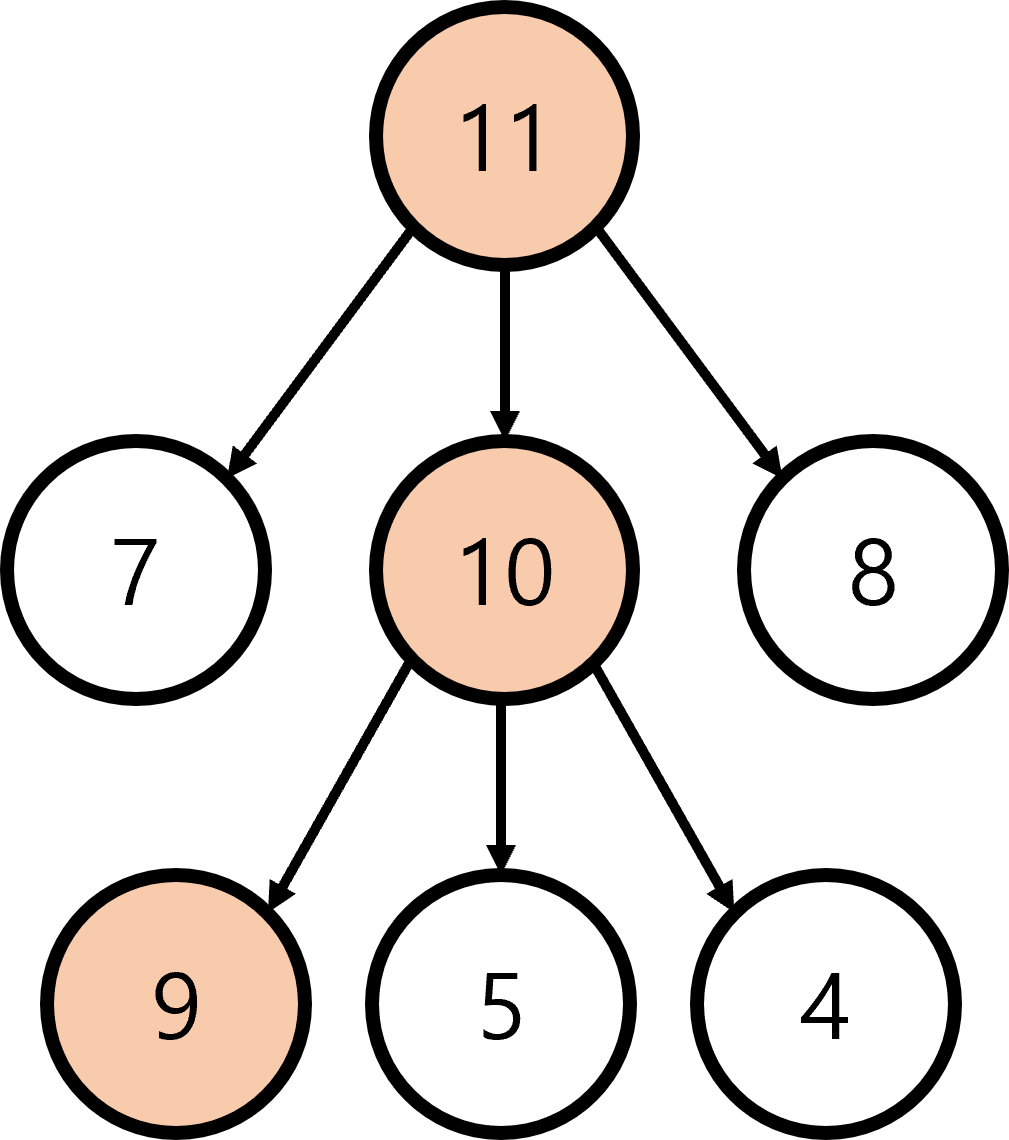
- 두 번째로 가장 큰 값을 갖는 9 노드를 선택한다.
- 따라서 그리디 알고리즘으로 문제를 풀면 총합이 30이며, 이는 최종적인 해답이 아니다.
- 문제에 따라 그리디 알고리즘을 적절히 활용해야 한다.
- 어떤 문제에 그리디 알고리즘을 적용하는 것이 좋을까?
정당성 증명
그리디 알고리즘으로 어떤 문제의 최종적인 해답을 찾아낼 수 있는지 알기 위해 두 가지 속성을 증명해야 한다.
1. 탐욕적 선택 속성(greedy choice property)
- 이전의 최적 선택이 이후의 최적 선택에 영향을 주지 않는 속성
2. 최적 부분 구조(optimal substructure)
- 전체 문제의 최적해가 부분 문제의 최적해로 구성되는 속성
예제 2의 정당성 증명
예제 2를 다시 살펴보자.
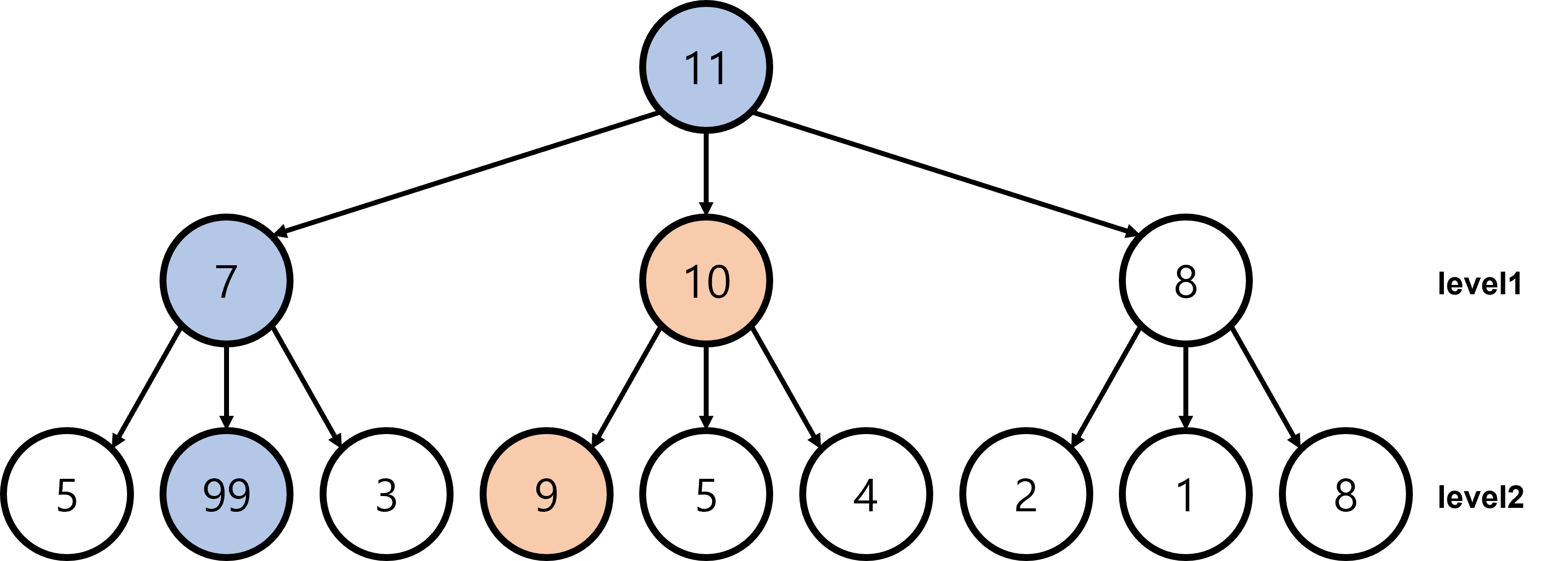
탐욕적 선택 속성(greedy choice property)
- 예제 2는 루트 노드에서 level1 노드를 선택하면, level2에서 마주할 노드의 값이 달라진다.
- 따라서 앞선 선택이 이후의 선택에 영향을 주므로, 이 문제는 탐욕적 선택 속성을 갖지 않는다. 예제 2는 그리디 알고리즘을 적용하기 부적절하다.
최적 부분 구조 (optimal substructure)
- 예제 2에서
선택 가능한 노드들 중 가장 큰 값의 노드를 선택와 같은 최적의 해를 골라도 최종적인 해답에 도달할 수 없었다. - 전체 문제의 최종적인 해답이 부분 문제의 최적해로 구성되지 않았기 때문이다. 최종적인 해답을 도달하기 위해서는 최적의 해를 고르지 않는 순간이 필요했다. 따라서 예제 2는 그리디 알고리즘을 적용하기 부적절하다.
참고자료
https://hanamon.kr/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%ED%83%90%EC%9A%95%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-greedy-algorithm/
https://loosie.tistory.com/515
https://velog.io/@kyunghwan1207/%EA%B7%B8%EB%A6%AC%EB%94%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98Greedy-Algorithm-%ED%83%90%EC%9A%95%EB%B2%95
