N-Queens 문제

8 퀸 문제는 8x8크기의 체스판에 퀸을 8개 배치하는 문제이다. 1848년 막스 베첼이 처음 제안하였다. 이 문제를 일반화하면 NxN 크기의 체스판에 퀸을 N개 배치하는 N 퀸 문제가 된다. 구성적인 해법으로 N이 2,3인경우를 제외하고 해를 찾을 수 있다.
N개의 판이 주어졌을 때 N-Queens의 갯수를 리턴하는 함수를 만드는 것이 이번 과제였다

계획

처음 N-Queens 문제를 받고 우리팀은 여러가지 계획을 의논하였다 의논하였던 아이디어는 아래와 같다

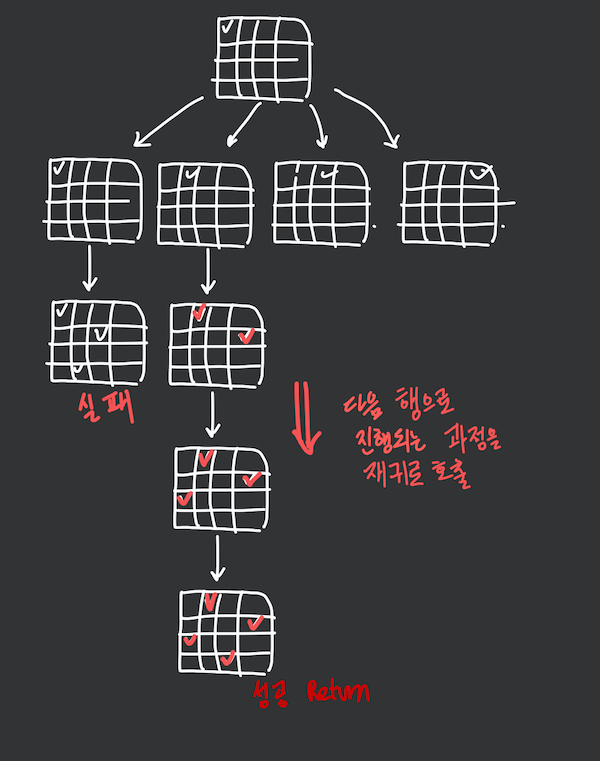
1. 재귀를 이용한 구현
   탈출 조건 : 탐색하는 과정 중 매개변수로 전달해준 행이 N과 같아질 때,퀸을 놓는 좌표가 범위에 있지 않을 때
   재귀 호출 : 매개변수인 행의 인덱스를 +1 하여 재귀를 호출한다.

2. 반복을 이용한 구현
   퀸을 놓고 빼는 과정을 배열에 저장하고 이를 반복문을 이용하여 충돌이 일어나는지 체크한다

위와 같이 두가지 아이디어가 나왔는데 두번째 방법의 문제점은 배열의 저장해야될 체스판의 경우의 수를 생각해보면 매우 비효율적이라 생각이 들어 재귀를 이용한 구현을 하기로 했다.

코드 작성

체스 보드와 관련된 함수들

Board                   ->  체스판 객체
_isInBounds()           ->  좌표가 체스판에 속하는지 확인하는 함수
togglePiece()           ->  퀸을 좌표에 두거나 뺄수 있는 함수
hasAnyQueensConflicts() ->  체스판에서 충돌이 일어나는지 확인하는 함수

초기 구현

countNQueensSolutions = function(n) {
  let board = new Board({ n: n });
  let count = 0;
  const recursion = (rowIndex) => {
    if (rowIndex === n) {
      count++;
      return count;
    }
    for (let i = 0; i < n; i++) {
      if (board._isInBounds(rowIndex, i)) {
        board.togglePiece(rowIndex, i);
        if (!board.hasAnyQueensConflicts()) {
          recursion(rowIndex + 1);
        }
        board.togglePiece(rowIndex, i);
      }
    }
  };
  recursion(0);
  return count;
}; 

성능 측정

위와 같은 방식으로 성능을 측정하였을 때 약 265ms 의 속도가 나왔다 내 생각으로는 퀸을 놓는 과정이 각 행마다 안놓아도 될 위치에서도 퀸을 놓는 과정이 이루어 지는 과정을 줄이면 어느정도 성능이개선될 것이라 생각이 들었다

성능 개선을 위한 시도

1. 인덱스를 매개변수로 넘겨주기
   이전에 놓은 인덱스를 매개변수로 넘겨주기 위해서 매개변수를 정의를 하였는데 이 매개변수의 개수를 정확히 몇개로 정의할 수 가 없어서 5개를 전달해주는 형식으로 아래와 같이 코딩을 하였다.

let board = new Board({ n: n });
  let count = 0;
  const recursion = (
    rowIndex,
    checkIndex1,
    checkIndex2,
    checkIndex3,
    checkIndex4,
    checkIndex5
  ) => {
    if (rowIndex === n) {
      count++;
      return count;
    }
    for (let i = 0; i < n; i++) {
      if (
        checkIndex1 !== i &&
        checkIndex2 !== i &&
        checkIndex3 !== i &&
        checkIndex4 !== i &&
        checkIndex5 !== i
      ) {
        if (board._isInBounds(rowIndex, i)) {
          board.togglePiece(rowIndex, i);
          if (!board.hasAnyQueensConflicts()) {
            recursion(
              rowIndex + 1,
              checkIndex2,
              checkIndex3,
              checkIndex4,
              checkIndex5,
              i
            );
          }
          board.togglePiece(rowIndex, i);
        }
      }
    }
  };
  recursion(0);
  return count;

성능적인 면에서는 좋아졌지만 n의 크기가 더욱 커지게 되면 커버할 수 있는 인덱스의 개수의 비율도 작아지기 때문에 만족하는 코드가 아니였다 가독성도 좋지 않다

2. 0으로 초기화된 배열을 이용

  let board = new Board({ n: n });
  let count = 0;

  let isTogglArr = Array(n).fill(0);
  const recursion = rowIndex => {
    if (rowIndex === n) {
      return count++;
    }
    for (let i = 0; i < n; i++) {
      if (isTogglArr[i] !== 1) {
        board.togglePiece(rowIndex, i);
        if (!board.hasAnyQueensConflicts()) {
          isTogglArr[i] = 1;
          recursion(rowIndex + 1);
        }
        isTogglArr[i] = 0;
        board.togglePiece(rowIndex, i);
      }
    }
  };
  recursion(0);
  return count;

n개에 배열에 맞춰서 유동적인 로직이 되어서 성능이 좋아졌고 가독성 또한 올라갔다 이와 같은 방식은 메모리 공간을 조금 더써서 그 효율을 높이는 방식인데 이러한 방식의 대표적인 예제로는 memoization이 있다

memoization reference: https://www.zerocho.com/category/JavaScript/post/579248728241b6f43951af19

결론

이번 스프린트를 진행하면서 완벽한 리펙토링은 없다는 것을 알게 되었고 로직을 어떻게 짜는 가에 따라서 그 성능또한 천차만별이라는 것을 뼈저리게 알게 되었다

출처 : https://ko.wikipedia.org/wiki/%EC%97%AC%EB%8D%9F_%ED%80%B8_%EB%AC%B8%EC%A0%9C