Tree
tree는 연결리스트, 배열과는 다른게 계층적 자료구조이다.
이런 구조를 사용하는 예시로는 파일 시스템,사전,네트워크 라우팅 알고리즘이 있다
구성요소로는 아래와 같은 부분이 있다
- root 노드
- child 노드
- Leat 노드
- edge
- data
트리는 항상 하나의 루트 노드를 가지고 있고 이 루트 노드는 자식 노드를 가질 수 있고 새롭게 생성된 자식 노드 또한 자식을 가질 수 있다 그림을 그려 보면 아래와 같다
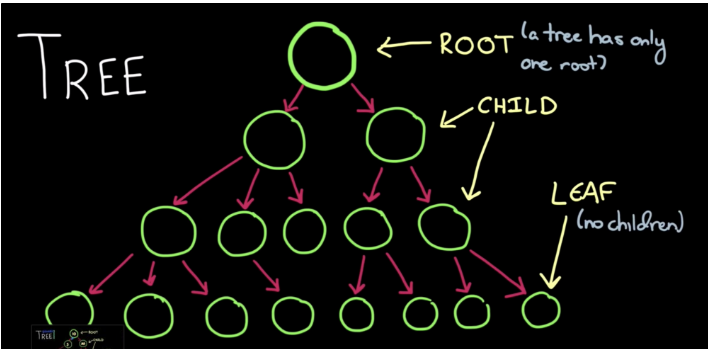
트리의 속성
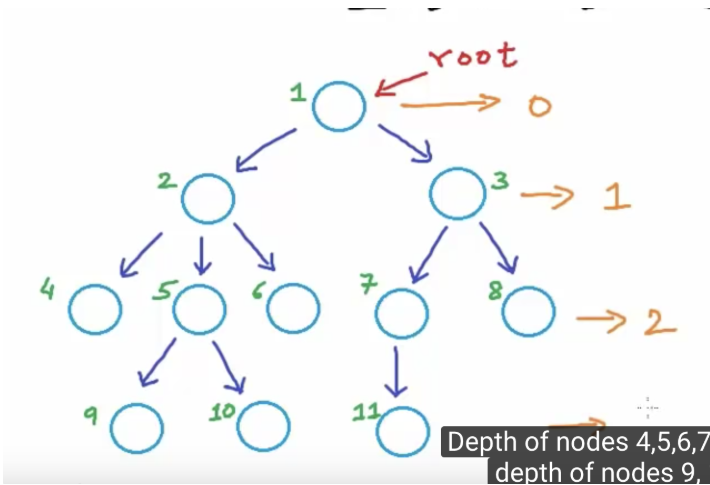
- Depth( 깊이 )
- x 노드의 깊이라는 것은 root노드 부터 x노드 까지의 edge의 개수를 말한다.
- 예를 들어 위 그림에서 5번 노드의 깊이는 root 부터 5번 노드까지 edge의 개수가 2개이므로 5번 노드의 깊이는 2가 된다
- Height( 높이 )
- x 노드의 높이라는 것은 x가 가진 leaf 노드 중에서 x까지의 길이가 가장 긴 길이를 말한다
- 예를 들어 2번 노드의 높이는 현재 2번 노드가 가지고 있는 leaf노드느 4,9,10,6 이고 이 중에서 x까지의 길이가 가장 긴 노드는 9,10이고 그 길이가 2가 되기 때문에 2번 노드의 높이는 2이다
트리의 메소드
.addChild()- 원하는 노드에 자식을 추가하는 메소드
- 자식이 배열의 형태로 저장이 되어있다면 새로운 노드를 만들어서 자식 노드 배열에 Push하는 형태로 구현이 가능할 것이다
.contains()- 매개변수가 해당 트리에 속해 있는지 확인하는 메소드
- 재귀를 이용해서 찾을 것 같다
Binary Search Tree
자식노드가 최대 2개까지만 붙는 트리를 Binary Tree라고 한다
Binary Tree의 구성요소
- Node
- data
- left : 왼쪽 노드의 정보를 가지고 있는 요소
- Right : 오른쪽 노드의 정보를 가지고 있는 요소
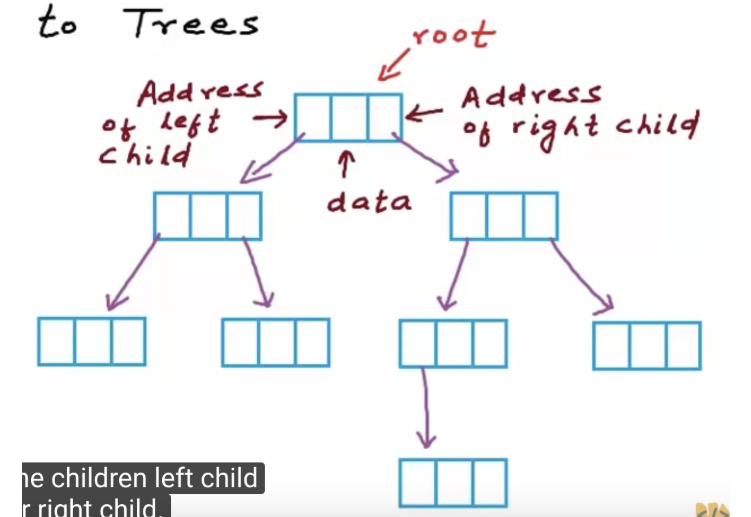
Binary Tree의 구현
- 동적 노드 생성 방식 : 이 방식은 일반적인 노드가 left,Right노드를 가지고 있는 방식이다
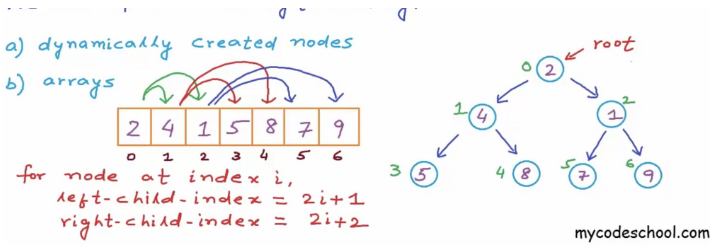
- 배열을 이용항 방식 : 이 방식은 배열의 인덱스를 이용한 방식이다
- left자식노드는 부모 인덱스가 i일 때 2i+1 이고
- Right 자식노드는 2i+2가 된다
- 이 방식은 heap 을 구현할 때 사용
Binary Tree의 종류
-
Compelete binary tree : 제일 마지막 층이 왼쪽 부터 채워진 트리
-
Full binary tree : 자식을 가지면 무조건 2개인 경우이거나 아예 없는 경우
-
Perfect Binary Tree : 모든 층이 가득차 있는 binary tree
-
Binary Search Tree : 부모노드의 왼쪽 자식과 오른쪽 자식이 일정한 정렬 규칙으로 정렬되어 있는 tree
Binary Tree의 순회
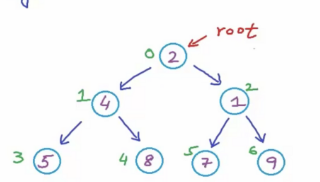
- preOrder(전위 순회) : 트리의 순회 순서가 Root, Left, Right 순서로 순회 하는 방식이다
- 순회 시 : 2 -> 4 -> 5 -> 8 -> 1 -> 7 -> 9
- inOrder(중위 순회) : 트리의 순회 순서가 Left, Root, Right 순서로 순회 하는 방식이다
- 순회 시 : 5 -> 4 -> 8 -> 2 -> 7 -> 1 -> 9
- postOrder(후위 순회) : 트리의 순회 순서가 Left, Right, Root 순서로 순회 하는 방식이다
- 순회 시 : 5 -> 8 -> 4 -> 7 -> 9 -> 1 -> 2
Binary Search Tree
자식노드가 최대 2개까지만 붙는 트리를 Binary Tree라고 하며 이 Binary Tree에서 약간의 규칙이 적용된 트리가 Binary Search Tree라고 한다 예시로는 아래의 그림이 있다
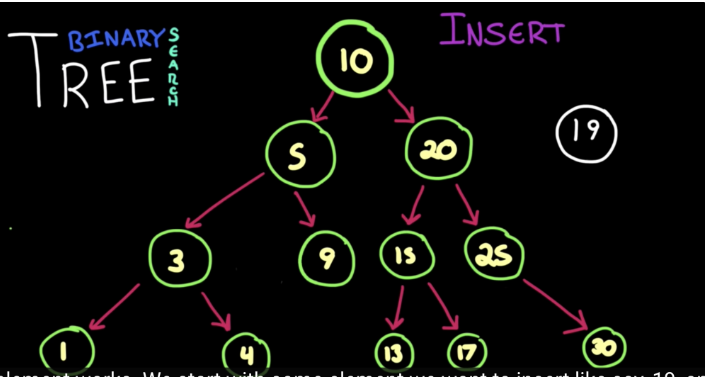
Binary Search Tree 메소드
search
- 이진트리의 순회 함수를 이용하여 data를 찾아낸다
insert
function insert(tree,node){
//node를 현재 tree의 value와 비교를 한다
//크다면 오른쪽 노드의 자식이 있는지 확인하고
// 있으면 insert 재귀호충 (tree -> right,node)
// 없으면 오른쪽 삽입
//작다면 왼쪽 노드의 자식이 있는지 확인하고
// 있으면 insert 재귀호충 (tree -> left,node)
// 없으면 왼쪽 삽입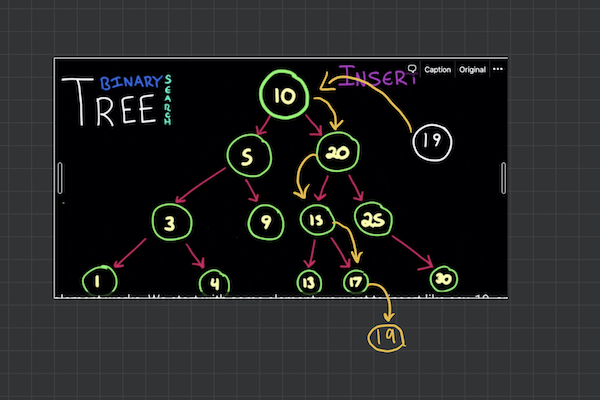
delete
-
삭제해야 될 노드가 자식이 없는 경우 : search 함수 알고리즘으로 노드를 찾아서 삭제해 주면 된다
-
삭제해야 될 노드의 자식이 하나인 경우
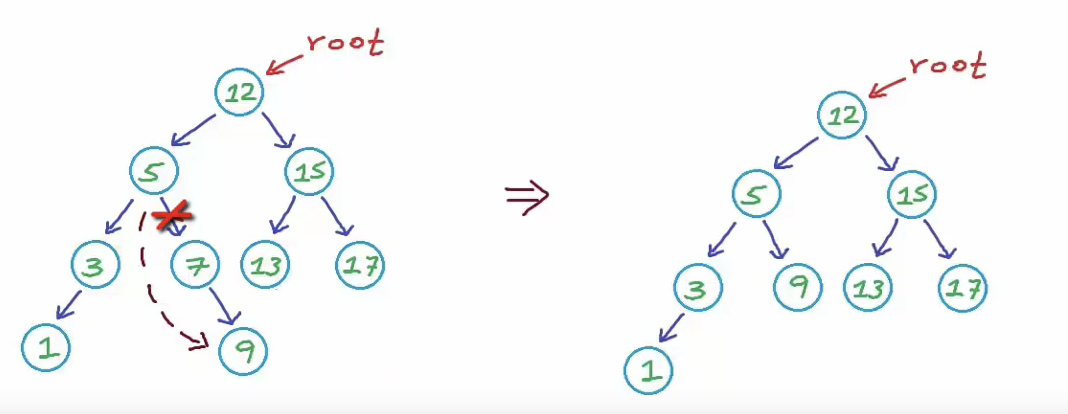
-
삭제해야 될 노드의 자식이 2개인 노드인 경우 방법이 두개가 있다
- 왼쪽 자식노드 중에 최대 값을 삭제한 자리에 대체한다 복사된 노드는 다시 삭제 함수를 호출하여 삭제한다
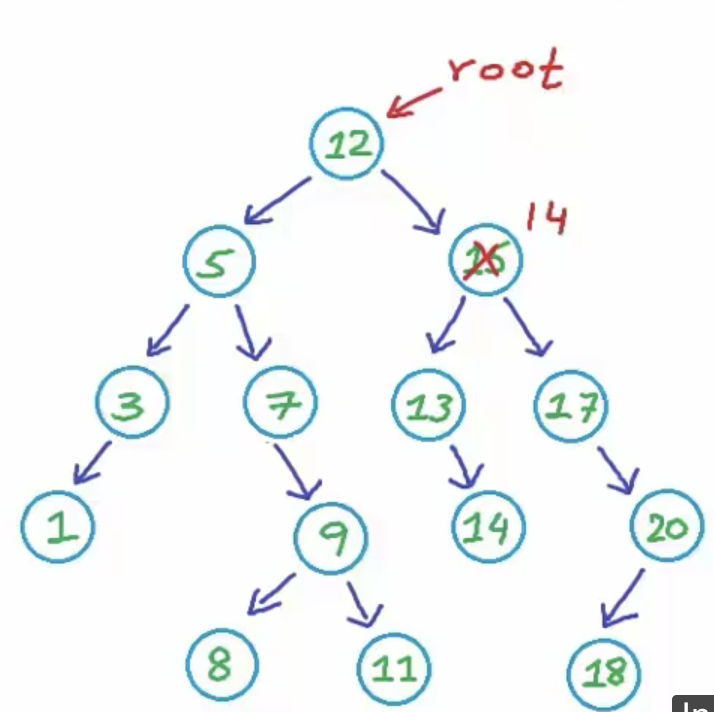
- 오른쪽 자식 노드 중에 최소 값을 삭제한 자리에 대체한다
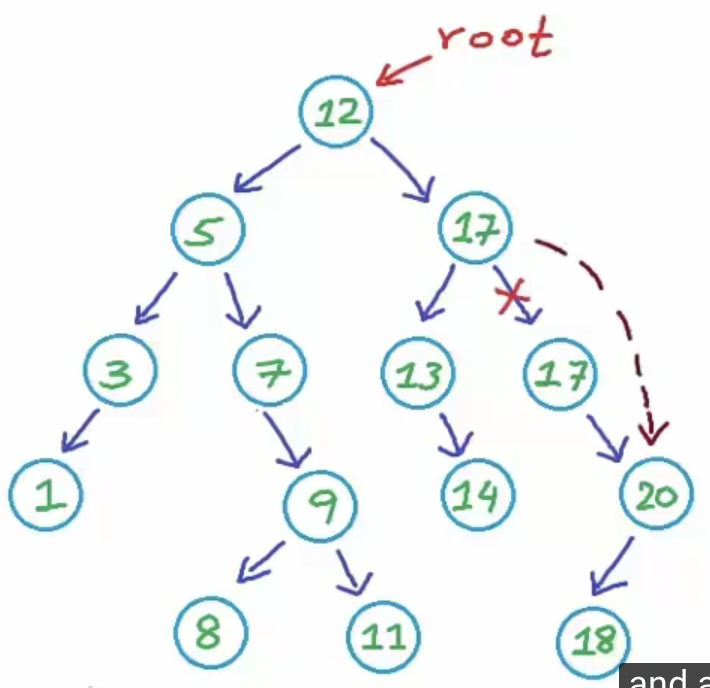
- 왼쪽 자식노드 중에 최대 값을 삭제한 자리에 대체한다 복사된 노드는 다시 삭제 함수를 호출하여 삭제한다